adding and subtracting radicals assignment

8.4 Add, Subtract, and Multiply Radical Expressions

Learning objectives.

By the end of this section, you will be able to:

• Add and subtract radical expressions
• Multiply radical expressions
• Use polynomial multiplication to multiply radical expressions

Be Prepared 8.10

Before you get started, take this readiness quiz.

Add: 3 x 2 + 9 x − 5 − ( x 2 − 2 x + 3 ) . 3 x 2 + 9 x − 5 − ( x 2 − 2 x + 3 ) . If you missed this problem, review Example 5.5 .

Be Prepared 8.11

Simplify: ( 2 + a ) ( 4 − a ) . ( 2 + a ) ( 4 − a ) . If you missed this problem, review Example 5.28 .

Be Prepared 8.12

Simplify: ( 9 − 5 y ) 2 . ( 9 − 5 y ) 2 . If you missed this problem, review Example 5.31 .

Add and Subtract Radical Expressions

Adding radical expressions with the same index and the same radicand is just like adding like terms. We call radicals with the same index and the same radicand like radicals to remind us they work the same as like terms.

Like Radicals

Like radicals are radical expressions with the same index and the same radicand.

We add and subtract like radicals in the same way we add and subtract like terms. We know that 3 x + 8 x 3 x + 8 x is 11 x . 11 x . Similarly we add 3 x + 8 x 3 x + 8 x and the result is 11 x . 11 x .

Think about adding like terms with variables as you do the next few examples. When you have like radicals, you just add or subtract the coefficients. When the radicals are not like, you cannot combine the terms.

Example 8.36

Simplify: ⓐ 2 2 − 7 2 2 2 − 7 2 ⓑ 5 y 3 + 4 y 3 5 y 3 + 4 y 3 ⓒ 7 x 4 − 2 y 4 . 7 x 4 − 2 y 4 .

The indices are the same but the radicals are different. These are not like radicals. Since the radicals are not like, we cannot subtract them.

Try It 8.71

Simplify: ⓐ 8 2 − 9 2 8 2 − 9 2 ⓑ 4 x 3 + 7 x 3 4 x 3 + 7 x 3 ⓒ 3 x 4 − 5 y 4 . 3 x 4 − 5 y 4 .

Try It 8.72

Simplify: ⓐ 5 3 − 9 3 5 3 − 9 3 ⓑ 5 y 3 + 3 y 3 5 y 3 + 3 y 3 ⓒ 5 m 4 − 2 m 3 . 5 m 4 − 2 m 3 .

For radicals to be like, they must have the same index and radicand. When the radicands contain more than one variable, as long as all the variables and their exponents are identical, the radicands are the same.

Example 8.37

Simplify: ⓐ 2 5 n − 6 5 n + 4 5 n 2 5 n − 6 5 n + 4 5 n ⓑ 3 x y 4 + 5 3 x y 4 − 4 3 x y 4 . 3 x y 4 + 5 3 x y 4 − 4 3 x y 4 .

Try It 8.73

Simplify: ⓐ 7 x − 7 7 x + 4 7 x 7 x − 7 7 x + 4 7 x ⓑ 4 5 x y 4 + 2 5 x y 4 − 7 5 x y 4 . 4 5 x y 4 + 2 5 x y 4 − 7 5 x y 4 .

Try It 8.74

Simplify: ⓐ 4 3 y − 7 3 y + 2 3 y 4 3 y − 7 3 y + 2 3 y ⓑ 6 7 m n 3 + 7 m n 3 − 4 7 m n 3 . 6 7 m n 3 + 7 m n 3 − 4 7 m n 3 .

Remember that we always simplify radicals by removing the largest factor from the radicand that is a power of the index. Once each radical is simplified, we can then decide if they are like radicals.

Example 8.38

Simplify: ⓐ 20 + 3 5 20 + 3 5 ⓑ 24 3 − 375 3 24 3 − 375 3 ⓒ 1 2 48 4 − 2 3 243 4 . 1 2 48 4 − 2 3 243 4 .

Try It 8.75

Simplify: ⓐ 18 + 6 2 18 + 6 2 ⓑ 6 16 3 − 2 250 3 6 16 3 − 2 250 3 ⓒ 2 3 81 3 − 1 2 24 3 . 2 3 81 3 − 1 2 24 3 .

Try It 8.76

Simplify: ⓐ 27 + 4 3 27 + 4 3 ⓑ 4 5 3 − 7 40 3 4 5 3 − 7 40 3 ⓒ 1 2 128 3 − 5 3 54 3 . 1 2 128 3 − 5 3 54 3 .

In the next example, we will remove both constant and variable factors from the radicals. Now that we have practiced taking both the even and odd roots of variables, it is common practice at this point for us to assume all variables are greater than or equal to zero so that absolute values are not needed. We will use this assumption throughout the rest of this chapter.

Example 8.39

Simplify: ⓐ 9 50 m 2 − 6 48 m 2 9 50 m 2 − 6 48 m 2 ⓑ 54 n 5 3 − 16 n 5 3 . 54 n 5 3 − 16 n 5 3 .

Try It 8.77

Simplify: ⓐ 32 m 7 − 50 m 7 32 m 7 − 50 m 7 ⓑ 135 x 7 3 − 40 x 7 3 . 135 x 7 3 − 40 x 7 3 .

Try It 8.78

Simplify: ⓐ 27 p 3 − 48 p 3 27 p 3 − 48 p 3 ⓑ 256 y 5 3 − 32 y 5 3 . 256 y 5 3 − 32 y 5 3 .

Multiply Radical Expressions

We have used the Product Property of Roots to simplify square roots by removing the perfect square factors. We can use the Product Property of Roots ‘in reverse’ to multiply square roots. Remember, we assume all variables are greater than or equal to zero.

We will rewrite the Product Property of Roots so we see both ways together.

Product Property of Roots

For any real numbers, a n a n and b n , b n , and for any integer n ≥ 2 n ≥ 2

When we multiply two radicals they must have the same index. Once we multiply the radicals, we then look for factors that are a power of the index and simplify the radical whenever possible.

Multiplying radicals with coefficients is much like multiplying variables with coefficients. To multiply 4 x · 3 y 4 x · 3 y we multiply the coefficients together and then the variables. The result is 12 xy . Keep this in mind as you do these examples.

Example 8.40

Simplify: ⓐ ( 6 2 ) ( 3 10 ) ( 6 2 ) ( 3 10 ) ⓑ ( −5 4 3 ) ( −4 6 3 ) . ( −5 4 3 ) ( −4 6 3 ) .

Try It 8.79

Simplify: ⓐ ( 3 2 ) ( 2 30 ) ( 3 2 ) ( 2 30 ) ⓑ ( 2 18 3 ) ( −3 6 3 ) . ( 2 18 3 ) ( −3 6 3 ) .

Try It 8.80

Simplify: ⓐ ( 3 3 ) ( 3 6 ) ( 3 3 ) ( 3 6 ) ⓑ ( −4 9 3 ) ( 3 6 3 ) . ( −4 9 3 ) ( 3 6 3 ) .

We follow the same procedures when there are variables in the radicands.

Example 8.41

Simplify: ⓐ ( 10 6 p 3 ) ( 4 3 p ) ( 10 6 p 3 ) ( 4 3 p ) ⓑ ( 2 20 y 2 4 ) ( 3 28 y 3 4 ) . ( 2 20 y 2 4 ) ( 3 28 y 3 4 ) .

ⓑ When the radicands involve large numbers, it is often advantageous to factor them in order to find the perfect powers.

Try It 8.81

Simplify: ⓐ ( 6 6 x 2 ) ( 8 30 x 4 ) ( 6 6 x 2 ) ( 8 30 x 4 ) ⓑ ( −4 12 y 3 4 ) ( − 8 y 3 4 ) . ( −4 12 y 3 4 ) ( − 8 y 3 4 ) .

Try It 8.82

Simplify: ⓐ ( 2 6 y 4 ) ( 12 30 y ) ( 2 6 y 4 ) ( 12 30 y ) ⓑ ( −4 9 a 3 4 ) ( 3 27 a 2 4 ) . ( −4 9 a 3 4 ) ( 3 27 a 2 4 ) .

Use Polynomial Multiplication to Multiply Radical Expressions

In the next a few examples, we will use the Distributive Property to multiply expressions with radicals. First we will distribute and then simplify the radicals when possible.

Example 8.42

Simplify: ⓐ 6 ( 2 + 18 ) 6 ( 2 + 18 ) ⓑ 9 3 ( 5 − 18 3 ) . 9 3 ( 5 − 18 3 ) .

Try It 8.83

Simplify: ⓐ 6 ( 1 + 3 6 ) 6 ( 1 + 3 6 ) ⓑ 4 3 ( −2 − 6 3 ) . 4 3 ( −2 − 6 3 ) .

Try It 8.84

Simplify: ⓐ 8 ( 2 − 5 8 ) 8 ( 2 − 5 8 ) ⓑ 3 3 ( − 9 3 − 6 3 ) . 3 3 ( − 9 3 − 6 3 ) .

When we worked with polynomials, we multiplied binomials by binomials. Remember, this gave us four products before we combined any like terms. To be sure to get all four products, we organized our work—usually by the FOIL method.

Example 8.43

Simplify: ⓐ ( 3 − 2 7 ) ( 4 − 2 7 ) ( 3 − 2 7 ) ( 4 − 2 7 ) ⓑ ( x 3 − 2 ) ( x 3 + 4 ) . ( x 3 − 2 ) ( x 3 + 4 ) .

Try It 8.85

Simplify: ⓐ ( 6 − 3 7 ) ( 3 + 4 7 ) ( 6 − 3 7 ) ( 3 + 4 7 ) ⓑ ( x 3 − 2 ) ( x 3 − 3 ) . ( x 3 − 2 ) ( x 3 − 3 ) .

Try It 8.86

Simplify: ⓐ ( 2 − 3 11 ) ( 4 − 11 ) ( 2 − 3 11 ) ( 4 − 11 ) ⓑ ( x 3 + 1 ) ( x 3 + 3 ) . ( x 3 + 1 ) ( x 3 + 3 ) .

Example 8.44

Simplify: ( 3 2 − 5 ) ( 2 + 4 5 ) . ( 3 2 − 5 ) ( 2 + 4 5 ) .

Try It 8.87

Simplify: ( 5 3 − 7 ) ( 3 + 2 7 ) ( 5 3 − 7 ) ( 3 + 2 7 )

Try It 8.88

Simplify: ( 6 − 3 8 ) ( 2 6 + 8 ) ( 6 − 3 8 ) ( 2 6 + 8 )

Recognizing some special products made our work easier when we multiplied binomials earlier. This is true when we multiply radicals, too. The special product formulas we used are shown here.

Special Products

We will use the special product formulas in the next few examples. We will start with the Product of Binomial Squares Pattern .

Example 8.45

Simplify: ⓐ ( 2 + 3 ) 2 ( 2 + 3 ) 2 ⓑ ( 4 − 2 5 ) 2 . ( 4 − 2 5 ) 2 .

Be sure to include the 2 a b 2 a b term when squaring a binomial.

Try It 8.89

Simplify: ⓐ ( 10 + 2 ) 2 ( 10 + 2 ) 2 ⓑ ( 1 + 3 6 ) 2 . ( 1 + 3 6 ) 2 .

Try It 8.90

Simplify: ⓐ ( 6 − 5 ) 2 ( 6 − 5 ) 2 ⓑ ( 9 − 2 10 ) 2 . ( 9 − 2 10 ) 2 .

In the next example, we will use the Product of Conjugates Pattern. Notice that the final product has no radical.

Example 8.46

Simplify: ( 5 − 2 3 ) ( 5 + 2 3 ) . ( 5 − 2 3 ) ( 5 + 2 3 ) .

Try It 8.91

Simplify: ( 3 − 2 5 ) ( 3 + 2 5 ) ( 3 − 2 5 ) ( 3 + 2 5 )

Try It 8.92

Simplify: ( 4 + 5 7 ) ( 4 − 5 7 ) . ( 4 + 5 7 ) ( 4 − 5 7 ) .

Access these online resources for additional instruction and practice with adding, subtracting, and multiplying radical expressions.

• Multiplying Adding Subtracting Radicals
• Multiplying Special Products: Square Binomials Containing Square Roots
• Multiplying Conjugates

Section 8.4 Exercises

Practice makes perfect.

In the following exercises, simplify.

ⓐ 8 2 − 5 2 8 2 − 5 2 ⓑ 5 m 3 + 2 m 3 5 m 3 + 2 m 3 ⓒ 8 m 4 − 2 m 4 8 m 4 − 2 m 4

ⓐ 7 2 − 3 2 7 2 − 3 2 ⓑ 7 p 3 + 2 p 3 7 p 3 + 2 p 3 ⓒ 5 x 3 − 3 x 3 5 x 3 − 3 x 3

ⓐ 3 5 + 6 5 3 5 + 6 5 ⓑ 9 a 3 + 3 a 3 9 a 3 + 3 a 3 ⓒ 5 2 z 4 + 2 z 4 5 2 z 4 + 2 z 4

ⓐ 4 5 + 8 5 4 5 + 8 5 ⓑ m 3 − 4 m 3 m 3 − 4 m 3 ⓒ n + 3 n n + 3 n

ⓐ 3 2 a − 4 2 a + 5 2 a 3 2 a − 4 2 a + 5 2 a ⓑ 5 3 a b 4 − 3 3 a b 4 − 2 3 a b 4 5 3 a b 4 − 3 3 a b 4 − 2 3 a b 4

ⓐ 11 b − 5 11 b + 3 11 b 11 b − 5 11 b + 3 11 b ⓑ 8 11 c d 4 + 5 11 c d 4 − 9 11 c d 4 8 11 c d 4 + 5 11 c d 4 − 9 11 c d 4

ⓐ 8 3 c + 2 3 c − 9 3 c 8 3 c + 2 3 c − 9 3 c ⓑ 2 4 p q 3 − 5 4 p q 3 + 4 4 p q 3 2 4 p q 3 − 5 4 p q 3 + 4 4 p q 3

ⓐ 3 5 d + 8 5 d − 11 5 d 3 5 d + 8 5 d − 11 5 d ⓑ 11 2 r s 3 − 9 2 r s 3 + 3 2 r s 3 11 2 r s 3 − 9 2 r s 3 + 3 2 r s 3

ⓐ 27 − 75 27 − 75 ⓑ 40 3 − 320 3 40 3 − 320 3 ⓒ 1 2 32 4 + 2 3 162 4 1 2 32 4 + 2 3 162 4

ⓐ 72 − 98 72 − 98 ⓑ 24 3 + 81 3 24 3 + 81 3 ⓒ 1 2 80 4 − 2 3 405 4 1 2 80 4 − 2 3 405 4

ⓐ 48 + 27 48 + 27 ⓑ 54 3 + 128 3 54 3 + 128 3 ⓒ 6 5 4 − 3 2 80 4 6 5 4 − 3 2 80 4

ⓐ 45 + 80 45 + 80 ⓑ 81 3 − 192 3 81 3 − 192 3 ⓒ 5 2 80 4 + 7 3 405 4 5 2 80 4 + 7 3 405 4

ⓐ 72 a 5 − 50 a 5 72 a 5 − 50 a 5 ⓑ 9 80 p 4 4 − 6 405 p 4 4 9 80 p 4 4 − 6 405 p 4 4

ⓐ 48 b 5 − 75 b 5 48 b 5 − 75 b 5 ⓑ 8 64 q 6 3 − 3 125 q 6 3 8 64 q 6 3 − 3 125 q 6 3

ⓐ 80 c 7 − 20 c 7 80 c 7 − 20 c 7 ⓑ 2 162 r 10 4 + 4 32 r 10 4 2 162 r 10 4 + 4 32 r 10 4

ⓐ 96 d 9 − 24 d 9 96 d 9 − 24 d 9 ⓑ 5 243 s 6 4 + 2 3 s 6 4 5 243 s 6 4 + 2 3 s 6 4

3 128 y 2 + 4 y 162 − 8 98 y 2 3 128 y 2 + 4 y 162 − 8 98 y 2

3 75 y 2 + 8 y 48 − 300 y 2 3 75 y 2 + 8 y 48 − 300 y 2

ⓐ ( −2 3 ) ( 3 18 ) ( −2 3 ) ( 3 18 ) ⓑ ( 8 4 3 ) ( −4 18 3 ) ( 8 4 3 ) ( −4 18 3 )

ⓐ ( −4 5 ) ( 5 10 ) ( −4 5 ) ( 5 10 ) ⓑ ( −2 9 3 ) ( 7 9 3 ) ( −2 9 3 ) ( 7 9 3 )

ⓐ ( 5 6 ) ( − 12 ) ( 5 6 ) ( − 12 ) ⓑ ( −2 18 4 ) ( − 9 4 ) ( −2 18 4 ) ( − 9 4 )

ⓐ ( −2 7 ) ( −2 14 ) ( −2 7 ) ( −2 14 ) ⓑ ( −3 8 4 ) ( −5 6 4 ) ( −3 8 4 ) ( −5 6 4 )

ⓐ ( 4 12 z 3 ) ( 3 9 z ) ( 4 12 z 3 ) ( 3 9 z ) ⓑ ( 5 3 x 3 3 ) ( 3 18 x 3 3 ) ( 5 3 x 3 3 ) ( 3 18 x 3 3 )

ⓐ ( 3 2 x 3 ) ( 7 18 x 2 ) ( 3 2 x 3 ) ( 7 18 x 2 ) ⓑ ( −6 20 a 2 3 ) ( −2 16 a 3 3 ) ( −6 20 a 2 3 ) ( −2 16 a 3 3 )

ⓐ ( −2 7 z 3 ) ( 3 14 z 8 ) ( −2 7 z 3 ) ( 3 14 z 8 ) ⓑ ( 2 8 y 2 4 ) ( −2 12 y 3 4 ) ( 2 8 y 2 4 ) ( −2 12 y 3 4 )

ⓐ ( 4 2 k 5 ) ( −3 32 k 6 ) ( 4 2 k 5 ) ( −3 32 k 6 ) ⓑ ( − 6 b 3 4 ) ( 3 8 b 3 4 ) ( − 6 b 3 4 ) ( 3 8 b 3 4 )

In the following exercises, multiply.

ⓐ 7 ( 5 + 2 7 ) 7 ( 5 + 2 7 ) ⓑ 6 3 ( 4 + 18 3 ) 6 3 ( 4 + 18 3 )

ⓐ 11 ( 8 + 4 11 ) 11 ( 8 + 4 11 ) ⓑ 3 3 ( 9 3 + 18 3 ) 3 3 ( 9 3 + 18 3 )

ⓐ 11 ( −3 + 4 11 ) 11 ( −3 + 4 11 ) ⓑ 3 4 ( 54 4 + 18 4 ) 3 4 ( 54 4 + 18 4 )

ⓐ 2 ( −5 + 9 2 ) 2 ( −5 + 9 2 ) ⓑ 2 4 ( 12 4 + 24 4 ) 2 4 ( 12 4 + 24 4 )

( 7 + 3 ) ( 9 − 3 ) ( 7 + 3 ) ( 9 − 3 )

( 8 − 2 ) ( 3 + 2 ) ( 8 − 2 ) ( 3 + 2 )

ⓐ ( 9 − 3 2 ) ( 6 + 4 2 ) ( 9 − 3 2 ) ( 6 + 4 2 ) ⓑ ( x 3 − 3 ) ( x 3 + 1 ) ( x 3 − 3 ) ( x 3 + 1 )

ⓐ ( 3 − 2 7 ) ( 5 − 4 7 ) ( 3 − 2 7 ) ( 5 − 4 7 ) ⓑ ( x 3 − 5 ) ( x 3 − 3 ) ( x 3 − 5 ) ( x 3 − 3 )

ⓐ ( 1 + 3 10 ) ( 5 − 2 10 ) ( 1 + 3 10 ) ( 5 − 2 10 ) ⓑ ( 2 x 3 + 6 ) ( x 3 + 1 ) ( 2 x 3 + 6 ) ( x 3 + 1 )

ⓐ ( 7 − 2 5 ) ( 4 + 9 5 ) ( 7 − 2 5 ) ( 4 + 9 5 ) ⓑ ( 3 x 3 + 2 ) ( x 3 − 2 ) ( 3 x 3 + 2 ) ( x 3 − 2 )

( 3 + 10 ) ( 3 + 2 10 ) ( 3 + 10 ) ( 3 + 2 10 )

( 11 + 5 ) ( 11 + 6 5 ) ( 11 + 5 ) ( 11 + 6 5 )

( 2 7 − 5 11 ) ( 4 7 + 9 11 ) ( 2 7 − 5 11 ) ( 4 7 + 9 11 )

( 4 6 + 7 13 ) ( 8 6 − 3 13 ) ( 4 6 + 7 13 ) ( 8 6 − 3 13 )

ⓐ ( 3 + 5 ) 2 ( 3 + 5 ) 2 ⓑ ( 2 − 5 3 ) 2 ( 2 − 5 3 ) 2

ⓐ ( 4 + 11 ) 2 ( 4 + 11 ) 2 ⓑ ( 3 − 2 5 ) 2 ( 3 − 2 5 ) 2

ⓐ ( 9 − 6 ) 2 ( 9 − 6 ) 2 ⓑ ( 10 + 3 7 ) 2 ( 10 + 3 7 ) 2

ⓐ ( 5 − 10 ) 2 ( 5 − 10 ) 2 ⓑ ( 8 + 3 2 ) 2 ( 8 + 3 2 ) 2

( 4 + 2 ) ( 4 − 2 ) ( 4 + 2 ) ( 4 − 2 )

( 7 + 10 ) ( 7 − 10 ) ( 7 + 10 ) ( 7 − 10 )

( 4 + 9 3 ) ( 4 − 9 3 ) ( 4 + 9 3 ) ( 4 − 9 3 )

( 1 + 8 2 ) ( 1 − 8 2 ) ( 1 + 8 2 ) ( 1 − 8 2 )

( 12 − 5 5 ) ( 12 + 5 5 ) ( 12 − 5 5 ) ( 12 + 5 5 )

( 9 − 4 3 ) ( 9 + 4 3 ) ( 9 − 4 3 ) ( 9 + 4 3 )

( 3 x 3 + 2 ) ( 3 x 3 − 2 ) ( 3 x 3 + 2 ) ( 3 x 3 − 2 )

( 4 x 3 + 3 ) ( 4 x 3 − 3 ) ( 4 x 3 + 3 ) ( 4 x 3 − 3 )

Mixed Practice

2 3 27 + 3 4 48 2 3 27 + 3 4 48

175 k 4 − 63 k 4 175 k 4 − 63 k 4

5 6 162 + 3 16 128 5 6 162 + 3 16 128

24 3 + / 81 3 24 3 + / 81 3

1 2 80 4 − 2 3 405 4 1 2 80 4 − 2 3 405 4

8 13 4 − 4 13 4 − 3 13 4 8 13 4 − 4 13 4 − 3 13 4

5 12 c 4 − 3 27 c 6 5 12 c 4 − 3 27 c 6

80 a 5 − 45 a 5 80 a 5 − 45 a 5

3 5 75 − 1 4 48 3 5 75 − 1 4 48

21 9 3 − 2 9 3 21 9 3 − 2 9 3

8 64 q 6 3 − 3 125 q 6 3 8 64 q 6 3 − 3 125 q 6 3

11 11 − 10 11 11 11 − 10 11

3 · 21 3 · 21

( 4 6 ) ( − 18 ) ( 4 6 ) ( − 18 )

( 7 4 3 ) ( −3 18 3 ) ( 7 4 3 ) ( −3 18 3 )

( 4 12 x 5 ) ( 2 6 x 3 ) ( 4 12 x 5 ) ( 2 6 x 3 )

( 29 ) 2 ( 29 ) 2

( −4 17 ) ( −3 17 ) ( −4 17 ) ( −3 17 )

( −4 + 17 ) ( −3 + 17 ) ( −4 + 17 ) ( −3 + 17 )

( 3 8 a 2 4 ) ( 12 a 3 4 ) ( 3 8 a 2 4 ) ( 12 a 3 4 )

( 6 − 3 2 ) 2 ( 6 − 3 2 ) 2

3 ( 4 − 3 3 ) 3 ( 4 − 3 3 )

3 3 ( 2 9 3 + 18 3 ) 3 3 ( 2 9 3 + 18 3 )

( 6 + 3 ) ( 6 + 6 3 ) ( 6 + 3 ) ( 6 + 6 3 )

Writing Exercises

Explain when a radical expression is in simplest form.

Explain the process for determining whether two radicals are like or unlike. Make sure your answer makes sense for radicals containing both numbers and variables.

ⓐ Explain why ( − n ) 2 ( − n ) 2 is always non-negative, for n ≥ 0 . n ≥ 0 . ⓑ Explain why − ( n ) 2 − ( n ) 2 is always non-positive, for n ≥ 0. n ≥ 0.

Use the binomial square pattern to simplify ( 3 + 2 ) 2 . ( 3 + 2 ) 2 . Explain all your steps.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/8-4-add-subtract-and-multiply-radical-expressions

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 9: Radicals

9.3 Adding and Subtracting Radicals

Adding and subtracting radicals is similar to adding and subtracting variables. The condition is that the variables, like the radicals, must be identical before they can be added or subtracted. Recall the addition and subtraction of like variables:

Example 9.3.1

Simplify [latex]4x^2 + 5x - 6x^2 + 3x - 2x[/latex].

First, we sort out like variables and reorder them to be combined.

[latex]\begin{array}{ll} & {4x}^{2} + 5x - 6x^{2} + 3x - 2x \\ \text{becomes}& {4x}^{2}-{6x}^{2}\text{ and }5x+3x-2x \end{array}[/latex]

Combining like variables yields:

[latex]-2x^2 + 6x[/latex]

When adding and subtracting radicals, follow the same logic. Radicals must be the same before they can be combined.

Example 9.3.2

Simplify [latex]5\sqrt{11} + 5\sqrt{13} - 2\sqrt{13} + 6\sqrt{11} - 2\sqrt{11}[/latex].

[latex]\begin{array}{ll} & 5\sqrt{11} + 5\sqrt{13} - 2\sqrt{13} + 6\sqrt{11} - 2\sqrt{11} \\ \text{becomes}& 5\sqrt{13}-2\sqrt{13}\text{ and }5\sqrt{11}+6\sqrt{11}-2\sqrt{11} \end{array}[/latex]

Combining like radicals yields:

[latex]3\sqrt{13} + 9\sqrt{11}[/latex]

Generally, it is required to simplify radicals before combining them. For example:

Example 9.3.3

Simplify [latex]4\sqrt{45} + 3\sqrt{18} - \sqrt{98} + 2\sqrt{20}[/latex].

All of these radicals need to be simplified before they can be combined.

[latex]\begin{array}{ll} & 4\sqrt{45}+3\sqrt{18}-\sqrt{98}+2\sqrt{20} \\ \text{becomes} & 4\sqrt{9\cdot 5}+3\sqrt{9\cdot 2} - \sqrt{49\cdot 2}+2\sqrt{5\cdot 4} \\ \text{simplifying to}& 4\cdot3\sqrt{5}+3\cdot 3\sqrt{2}-7\sqrt{2}+2\cdot 2\sqrt{5} \\ \text{and reduces to}&12\sqrt{5}+9\sqrt{2}-7\sqrt{2}+4\sqrt{5} \end{array}[/latex]

Recombining these so they can be added and subtracted yields:

[latex]12\sqrt{5}+4\sqrt{5}\text{ and }9\sqrt{2}-7\sqrt{2}[/latex]

[latex]16\sqrt{5} + 2\sqrt{2}[/latex]

Higher order radicals are treated in the same fashion as square roots. For example:

Example 9.3.4

Simplify [latex]4\sqrt[3]{54} - 9\sqrt[3]{16} + 5\sqrt[3]{9}[/latex].

Like example 9.3.3, these radicals need to be simplified before they can be combined.

[latex]\begin{array}{ll} & 4 \sqrt[3]{54} - 9 \sqrt[3]{16} + 5 \sqrt[3]{9} \\ \text{becomes} & 4 \sqrt[3]{27\cdot 2} - 9 \sqrt[3]{8\cdot 2} + 5 \sqrt[3]{9} \\ \text{simplifying to} & 4 \cdot 3 \sqrt[3]{2} - 9 \cdot 2 \sqrt[3]{2} + 5 \sqrt[3]{9} \\ \text{and reduces to}& 12 \sqrt[3]{2} - 18 \sqrt[3]{2} + 5 \sqrt[3]{9} \end{array}[/latex]

[latex]5\sqrt[3]{9} - 6\sqrt[3]{2}[/latex]

• [latex]2\sqrt{5}+2\sqrt{5}+2\sqrt{5}[/latex]
• [latex]-3\sqrt{6}-3\sqrt{3}-2\sqrt{3}[/latex]
• [latex]-3\sqrt{2}+3\sqrt{5}+3\sqrt{5}[/latex]
• [latex]-2\sqrt{6}-\sqrt{3}-3\sqrt{6}[/latex]
• [latex]2\sqrt{2}-3\sqrt{18}-\sqrt{2}[/latex]
• [latex]-\sqrt{54}-3\sqrt{6}+3\sqrt{27}[/latex]
• [latex]-3\sqrt{6}-\sqrt{12}+3\sqrt{3}[/latex]
• [latex]-\sqrt{5}-\sqrt{5}-2\sqrt{54}[/latex]
• [latex]3\sqrt{2}+2\sqrt{8}-3\sqrt{18}[/latex]
• [latex]2\sqrt{20}+2\sqrt{20}-\sqrt{3}[/latex]
• [latex]3\sqrt{18}-\sqrt{2}-3\sqrt{2}[/latex]
• [latex]-3\sqrt{27}+2\sqrt{3}-\sqrt{12}[/latex]
• [latex]-3\sqrt{6}-3\sqrt{6}-\sqrt{3}+3\sqrt{6}[/latex]
• [latex]-2\sqrt{2}-\sqrt{2}+3\sqrt{8}+3\sqrt{6}[/latex]
• [latex]-2\sqrt{18}-3\sqrt{8}-\sqrt{20}+2\sqrt{20}[/latex]
• [latex]-3\sqrt{18}-\sqrt{8}+2\sqrt{8}+2\sqrt{8}[/latex]
• [latex]-2\sqrt{24}-2\sqrt{6}+2\sqrt{6}+2\sqrt{20}[/latex]
• [latex]-3\sqrt{8}-\sqrt{5}-3\sqrt{6}+2\sqrt{18}[/latex]
• [latex]3\sqrt{24}-3\sqrt{27}+2\sqrt{6}+2\sqrt{8}[/latex]
• [latex]2\sqrt{6}-\sqrt{54}-3\sqrt{27}-\sqrt{3}[/latex]

Answer Key 9.3

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Adding and Subtracting Radicals

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Graphing Calculator Videos
• Calculator Keystroke Guide
• Figures and Formulas

Chapter R Resources

Section Resources

• Exercise Videos
• Lecture Videos
• Connect2 Intermediate Algebra
• eProfessors

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Roots and Radicals

Adding and Subtracting Radical Expressions

The steps in adding and subtracting Radical are:

Step 1. Simplify radicals. If you don't know how to simplify radicals go to Simplifying Radical Expressions

Step 2. Combine like radicals.

Example 1: Add or subtract to simplify radical expression: $ 2 \sqrt{12} + \sqrt{27}$

Step 1: Simplify radicals

Step 2: Combine like radicals

Exercise 1: Add or subtract to simplify

Here the radicands differ and are already simplified, so this expression cannot be simplified.

Adding and Subtracting Radicals with Fractions

Exercise 2: Add or subtract to simplify radical expression

• Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
• Complex Numbers Arithmetic Polar representation
• Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
• Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
• Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
• Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
• Exponential Functions Introduction Exponential Equations Logarithmic Functions
• Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
• Progressions Arithmetic Progressions Geometric Progressions
• Differentiation Common formulas Product and Quotient Rule Chain Rule
• Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
• Integrals Integration Formulas Exercises
• Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
• Integral Applications Area Volume Arc Length

Analytic geometry

• Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
• Conic Sections Circle Ellipse Hyperbola
• Analytic Geometry 3D Line in 3D Planes

Linear Algebra

• Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
• Determinants Introduction to Determinants Applications of Determinants
• Vectors Basic Operations Dot Product Cross Product

Random Quote

If you think dogs can't count, try putting three dog biscuits in your pocket and then giving Fido only two of them.

Phil Pastoret

If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.

John Louis von Neumann

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Add and Subtract Radicals

Adding and subtracting radical expressions.

You could probably still remember when your algebra teacher taught you how to combine like terms. The goal is to add or subtract variables as long as they “look” the same. Otherwise, we just have to keep them unchanged. For a quick review, let’s simplify the following algebraic expressions by combining like terms.

Simplifying Algebraic Expressions by Combining Like Terms

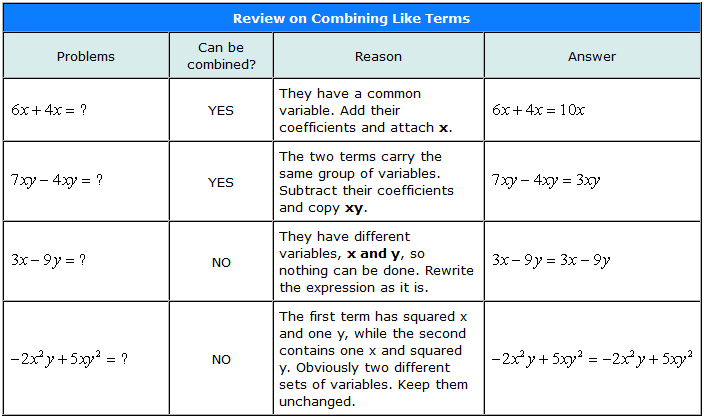
Now, just like combining like terms, you can add or subtract radical expressions if they have the same radical component. Since we are only dealing with square roots in this lesson, the only thing we have to worry about is to make sure that the radicand (stuff inside the radical symbol) are similar terms.

Let’s go over some examples to see them in action!

Examples of How to Add and Subtract Radical Expressions

Example 1: Simplify by adding and/or subtracting the radical expressions below.

Observe that each of the radicands doesn’t have a perfect square factor. This shows that they are already in their simplest form. The next step is to combine “like” radicals in the same way we combine similar terms.

I will rearrange the problem by placing similar radicals side by side to guide me in adding or subtracting appropriate radical expressions correctly. Maybe you can think of this as adding/subtracting the “coefficients” of like radical expressions.

The calculator agrees with our answer.

Example 2: Simplify by adding and/or subtracting the radical expressions below.

We can combine the two terms with [latex]\sqrt {13}[/latex] . The one with [latex]\sqrt 6[/latex]  will simply be carried along because there is nothing we can combine it with.

Rearrange the terms such that similar radicals are placed side by side for easy calculation.

The calculator gives us the same result. Great!

Example 3: Simplify the radical expressions below.

The first thing I would do is combine the obvious similar radicals, which in this case, the expressions with [latex]\sqrt {32}[/latex] .

I realize that the radical [latex]\sqrt 2[/latex]  is in its simplest form; however, the two radicals [latex]\sqrt {24}[/latex] and [latex]\sqrt {32}[/latex] need some simplification first. If you need a refresher on how to simplify radical expressions, check out my separate tutorial on simplifying radical expressions.

To simplify radical expressions, the key step is to always find the largest perfect square factor of the given radicand . Next, break them into a product of smaller square roots, and simplify.

  You can have something like this table on your scratch paper.

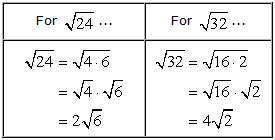
After simplifying the radical expressions in our side calculation, as shown above, we can now proceed as usual.

I will incorporate the simplification of radicals in the overall solution. I use some color coding to help you follow how the radicands are factored out, broken down into smaller radicals and simplified.

Yep! Our calculator yields the same answer.

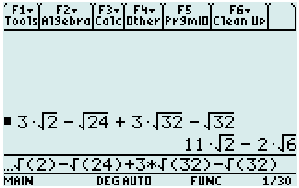
Example 4: Add and subtract the radical expressions below.

First off, I will combine the radical expressions with [latex]\sqrt 3[/latex].

Now, deal with radicands that have perfect square factors. We know that they can be simplified further.

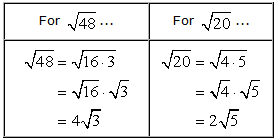
That side calculation above should help us finish our solution.

Checking our answer with a calculator, the answer above is correct! Notice that addition is commutative. That means the order of addition does not affect the final value.

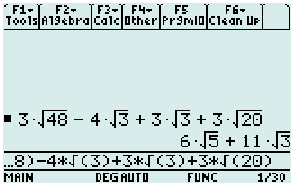
Example 5: Add and subtract the radical expressions below.

• Combine first the radical expressions with [latex]\sqrt {32}[/latex]
• Break down the radicands with perfect square factors, and simplify. The final answer is reduced to a single radical expression.
• Calculator check. We got it again!

Example 6: Simplify by combining the radical expressions below.

Example 7: Add and subtract to simplify the radical expressions below.

Example 8: Add and subtract to simplify the radical expressions below.

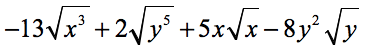
Here, we have variables inside the radical symbol. To simplify this, remember the concept that the square root of a squared term, either numerical or variable, is just the term itself. For quick examples…

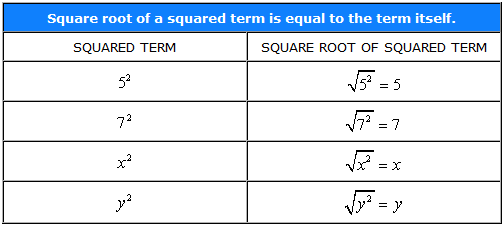
Therefore, the approach is to express (as much as possible) each variable raised to some power as products of a variable with an exponent of 2  because this allows us to easily get the square root. Now back to the problem…

Example 9: Add and subtract to simplify the radical expressions below.

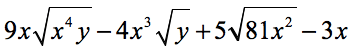
It seems that all radical expressions are different from each other. First, let’s simplify the radicals, and hopefully, something would come out nicely by having “like” radicals that we can add or subtract.

Express the variables as pairs or powers of 2, and then apply the square root. Here we go!

Example 10: Simplify the radical expressions below.

There are no obvious “like” radicals that we can add or subtract. Simplify each radical expression, and observe what we can do from that point.

We are able to generate “like” radicals that we can ultimately add or subtract to simplify our final answer.

You may also be interested in these related math lessons or tutorials:

Solving Radical Equations

Simplifying Radical Expressions

Multiplying Radical Expressions

Rationalizing the Denominator

Module 18: Roots and Rational Exponents

Adding and subtracting radicals, learning outcomes.

• Identify radicals that can be added or subtracted
• Add and subtract radical expressions

Adding and subtracting radicals is much like combining like terms with variables.  We can add and subtract expressions with variables like this:

[latex]5x+3y - 4x+7y=x+10y[/latex]

There are two keys to combining radicals by addition or subtraction: look at the index , and look at the radicand . If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals.

Remember the index is the degree of the root and the radicand is the term or expression under the radical. In the diagram below, the index is n, and the radicand is [latex]100[/latex].  The radicand is placed under the root symbol and the index is placed outside the root symbol to the left:

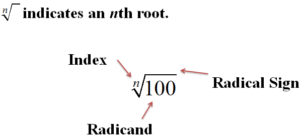
Index and radicand

In the graphic below, the index of the expression [latex]12\sqrt[3]{xy}[/latex] is [latex]3[/latex] and the radicand is [latex]xy[/latex].

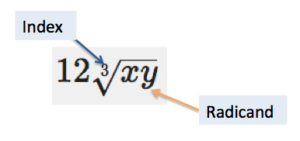
Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.

Identify the roots that have the same index and radicand.

[latex] 10\sqrt{6}[/latex]

[latex] -1\sqrt[3]{6}[/latex]

[latex] \sqrt{25}[/latex]

[latex] 12\sqrt{6}[/latex]

[latex] \frac{1}{2}\sqrt[3]{25}[/latex]

[latex] -7\sqrt[3]{6}[/latex]

Let’s start with [latex] 10\sqrt{6}[/latex].  The index is [latex]2[/latex] because no root was specified, and the radicand is [latex]6[/latex]. The only other radical that has the same index and radicand is [latex] 12\sqrt{6}[/latex].

[latex] -1\sqrt[3]{6}[/latex] has an index of [latex]3[/latex], and a radicand of [latex]6[/latex]. The only other radical that has the same index and radicand is [latex] -7\sqrt[3]{6}[/latex].

[latex] \sqrt{25}[/latex] has an index of [latex]2[/latex] and a radicand of [latex]25[/latex].  There are no other radicals in the list that have the same index and radicand.

[latex] 12\sqrt{6}[/latex] has the same index and radicand as [latex]10\sqrt{6}[/latex]

[latex] \frac{1}{2}\sqrt[3]{25}[/latex] has an index of [latex]3[/latex] and a radicand of [latex]25[/latex].  There are no other radicals in the list that share these.

[latex] -7\sqrt[3]{6}[/latex] has the same index and radicand as [latex] -1\sqrt[3]{6}[/latex]

Making sense of a string of radicals may be difficult. One helpful tip is to think of radicals as variables, and treat them the same way. When you add and subtract variables, you look for like terms, which is the same thing you will do when you add and subtract radicals.

Let’s use this concept to add some radicals.

In this first example, both radicals have the same radicand and index.

Add. [latex] 3\sqrt{11}+7\sqrt{11}[/latex]

[latex] \text{3}\sqrt{11}\text{ + 7}\sqrt{11}[/latex]

[latex] 3\sqrt{11}+7\sqrt{11}=10\sqrt{11}[/latex]

It may help to think of radical terms with words when you are adding and subtracting them. The last example could be read “three square roots of eleven plus [latex]7[/latex] square roots of eleven”.

This next example contains more addends, or terms that are being added together. Notice how you can combine like terms (radicals that have the same root and index) but you cannot combine unlike terms.

Add. [latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}[/latex]

[latex] 5\sqrt{2}+2\sqrt{2}+\sqrt{3}+4\sqrt{3}[/latex]

[latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}=7\sqrt{2}+5\sqrt{3}[/latex]

Notice that the expression in the previous example is simplified even though it has two terms: [latex] 7\sqrt{2}[/latex] and [latex] 5\sqrt{3}[/latex]. It would be a mistake to try to combine them further! (Some people make the mistake that [latex] 7\sqrt{2}+5\sqrt{3}=12\sqrt{5}[/latex]. This is incorrect because[latex] \sqrt{2}[/latex] and [latex]\sqrt{3}[/latex] are not like radicals so they cannot be added.)

Add. [latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}[/latex]

[latex] 3\sqrt{x}+\sqrt{x}+12\sqrt[3]{xy}[/latex]

[latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}=4\sqrt{x}+12\sqrt[3]{xy}[/latex]

In the following video, we show more examples of how to identify and add like radicals.

Sometimes you may need to add and simplify the radical. If the radicals are different, try simplifying first—you may end up being able to combine the radicals at the end, as shown in these next two examples.

Add and simplify. [latex] 2\sqrt[3]{40}+\sqrt[3]{135}[/latex]

[latex] \begin{array}{r}2\sqrt[3]{8\cdot 5}+\sqrt[3]{27\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}\cdot 5}+\sqrt[3]{{{(3)}^{3}}\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}}\cdot \sqrt[3]{5}+\sqrt[3]{{{(3)}^{3}}}\cdot \sqrt[3]{5}\end{array}[/latex]

[latex] 2\cdot 2\cdot \sqrt[3]{5}+3\cdot \sqrt[3]{5}[/latex]

[latex]4\sqrt[3]{5}+3\sqrt[3]{5}[/latex]

[latex] 2\sqrt[3]{40}+\sqrt[3]{135}=7\sqrt[3]{5}[/latex]

Add and simplify. [latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}[/latex]

[latex]\begin{array}{r}x\sqrt[3]{x\cdot {{y}^{3}}\cdot y}+y\sqrt[3]{{{x}^{3}}\cdot x\cdot y}\\x\sqrt[3]{{{y}^{3}}}\cdot \sqrt[3]{xy}+y\sqrt[3]{{{x}^{3}}}\cdot \sqrt[3]{xy}\\xy\cdot \sqrt[3]{xy}+xy\cdot \sqrt[3]{xy}\end{array}[/latex]

Add like radicals.

[latex] xy\sqrt[3]{xy}+xy\sqrt[3]{xy}[/latex]

[latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}=2xy\sqrt[3]{xy}[/latex]

The following video shows more examples of adding radicals that require simplification.

Subtracting Radicals

Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices (plural of index) must be the same for two (or more) radicals to be subtracted.  In the examples that follow, subtraction has been rewritten as addition of the opposite.

Subtract. [latex] 5\sqrt{13}-3\sqrt{13}[/latex]

[latex] 5\sqrt{13}-3\sqrt{13}[/latex]

[latex] 5\sqrt{13}-3\sqrt{13}=2\sqrt{13}[/latex]

Subtract. [latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}[/latex]

[latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}\\4\sqrt[3]{5a}-2\sqrt[3]{5a})-\sqrt[3]{3a})[/latex]

Combine. Although the indices of [latex] 2\sqrt[3]{5a}[/latex] and [latex] -\sqrt[3]{3a}[/latex] are the same, the radicands are not—so they cannot be combined.

[latex] 2\sqrt[3]{5a}-\sqrt[3]{3a})[/latex]

[latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}=2\sqrt[3]{5a}-\sqrt[3]{3a}[/latex]

In the video examples that follow, we show more examples of how to add and subtract radicals that don’t need to be simplified beforehand.

Subtract and simplify. [latex] 5\sqrt[4]{{{a}^{5}}b}-a\sqrt[4]{16ab}[/latex], where [latex]a\ge 0[/latex] and [latex]b\ge 0[/latex]

Simplify each radical by identifying and pulling out powers of [latex]4[/latex].

[latex]\begin{array}{r}5\sqrt[4]{{{a}^{4}}\cdot a\cdot b}-a\sqrt[4]{{{(2)}^{4}}\cdot a\cdot b}\\5\cdot a\sqrt[4]{a\cdot b}-a\cdot 2\sqrt[4]{a\cdot b}\\5a\sqrt[4]{ab}-2a\sqrt[4]{ab}\end{array}[/latex]

The answer is [latex]3a\sqrt[4]{ab}[/latex].

In our last videos, we show more examples of subtracting radicals that require simplifying.

Combining radicals is possible when the index and the radicand of two or more radicals are the same. Radicals with the same index and radicand are known as like radicals. It is often helpful to treat radicals just as you would treat variables: like radicals can be added and subtracted in the same way that like variables can be added and subtracted. Sometimes, you will need to simplify a radical expression before it is possible to add or subtract like terms.

Contribute!

Improve this page Learn More

• Screenshot: keys. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Index and radicand. Provided by : Lumen Learning. License : CC BY: Attribution
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/ . License : CC BY: Attribution
• Ex: Add and Subtract Radicals - No Simplifying. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/5pVc44dEsTI . License : CC BY: Attribution
• Ex: Add and Subtract Square Roots. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/tJk6_7lbrlw . License : CC BY: Attribution

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: Adding and Subtracting Radical Expressions

• Last updated
• Save as PDF
• Page ID 59895

Learning Objectives

• Add and subtract like radicals.
• Simplify radical expressions involving like radicals.

Adding and Subtracting Like Radicals

Adding and subtracting radical expressions is similar to adding and subtracting like terms. Radicals are considered to be like radicals 16 , or similar radicals 17 , when they share the same index and radicand. For example, the terms \(2\sqrt{6}\) and \(5\sqrt{6}\) contain like radicals and can be added using the distributive property as follows:

\(\begin{aligned} 2 \sqrt { 6 } + 5 \sqrt { 6 } & = ( 2 + 5 ) \sqrt { 6 } \\ & = 7 \sqrt { 6 } \end{aligned}\)

Typically, we do not show the step involving the distributive property and simply write,

\(2 \sqrt { 6 } + 5 \sqrt { 6 } = 7 \sqrt { 6 }\)

When adding terms with like radicals, add only the coefficients; the radical part remains the same.

Example \(\PageIndex{1}\):

Add: \(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 }\).

The terms are like radicals; therefore, add the coefficients.

\(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 } = 10 \sqrt [ 3 ] { 5 }\)

\(10 \sqrt [ 3 ] { 5 }\)

Subtraction is performed in a similar manner.

Example \(\PageIndex{2}\):

Subtract: \(4 \sqrt { 10 } - 5 \sqrt { 10 }\).

\(\begin{aligned} 4 \sqrt { 10 } - 5 \sqrt { 10 } & = ( 4 - 5 ) \sqrt { 10 } \\ & = - 1 \sqrt { 10 } \\ & = - \sqrt { 10 } \end{aligned}\)

\(- \sqrt { 10 }\)

If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.

Example \(\PageIndex{3}\):

Simplify: \(10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 }\).

\(\begin{aligned} 10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 } & = \color{Cerulean}{10 \sqrt { 5 } - 9 \sqrt { 5 }}\color{black}{ +}\color{OliveGreen}{ 6 \sqrt { 2 } - 7 \sqrt { 2 }} \\ & = \sqrt { 5 } - \sqrt { 2 } \end{aligned}\)

We cannot simplify any further because \(\sqrt{5}\) and \(\sqrt{2}\) are not like radicals; the radicands are not the same.

\(\sqrt { 5 } - \sqrt { 2 }\)

\(\color{YellowOrange}{\text{Caution:}}\) It is important to point out that \(\sqrt { 5 } - \sqrt { 2 } \neq \sqrt { 5 - 2 }\). We can verify this by calculating the value of each side with a calculator.

\(\begin{array} { c } { \sqrt { 5 } - \sqrt { 2 } \approx 0.82 } \\ { \sqrt { 5 - 2 } = \sqrt { 3 } \approx 1.73 } \end{array}\)

In general, note that \(\sqrt [ n ] { a } \pm \sqrt [ n ] { b } \neq \sqrt [ n ] { a \pm b }\).

Example \(\PageIndex{4}\):

Simplify: \(5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 }\).

\(\begin{aligned} 5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 } & =\color{Cerulean}{ 5 \sqrt [ 3 ] { 10 } - \sqrt [ 3 ] { 10 }}\color{black}{ +}\color{OliveGreen}{ 3 \sqrt { 10 } - 2 \sqrt { 10 }} \\ & = 4 \sqrt [ 3 ] { 10 } + \sqrt { 10 } \end{aligned}\)

We cannot simplify any further, because \(\sqrt [ 3 ] { 10 }\) and \(\sqrt { 10 }\) are not like radicals; the indices are not the same.

\(4 \sqrt [ 3 ] { 10 } + \sqrt { 10 }\)

Adding and Subtracting Radical Expressions

Often, we will have to simplify before we can identify the like radicals within the terms.

Example \(\PageIndex{5}\):

Subtract: \(\sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 }\).

At first glance, the radicals do not appear to be similar. However, after simplifying completely, we will see that we can combine them.

\(\begin{aligned} \sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 } & = \sqrt { 16 } \cdot 2 - \sqrt { 9 \cdot 2 } + \sqrt { 25 \cdot 2 } \\ & = 4 \sqrt { 2 } - 3 \sqrt { 2 } + 5 \sqrt { 2 } \\ & = 6 \sqrt { 2 } \end{aligned}\)

\(6\sqrt{2}\)

Example \(\PageIndex{6}\):

Simplify: \(\sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 }\).

Begin by looking for perfect cube factors of each radicand.

\(\begin{aligned} \sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 } & = \sqrt [ 3 ] { 27 \cdot 4 } + \sqrt [ 3 ] { 8 \cdot 3 } - \sqrt [ 3 ] { 8 \cdot 4 } - \sqrt [ 3 ] { 27 \cdot 3 }\quad\color{Cerulean}{Simplify.} \\ & = 3 \sqrt [ 3 ] { 4 } + \color{Cerulean}{2 \sqrt [ 3 ] { 3 } }\color{black}{-} 2 \sqrt [ 3 ] { 4 } - \color{Cerulean}{3 \sqrt [ 3 ] { 3 }} \quad\quad\quad\quad\quad\color{Cerulean}{Combine\:like\:terms.} \\ & = \sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 } \end{aligned}\)

\(\sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 }\)

Exercise \(\PageIndex{1}\)

Simplify: \(\sqrt { 20 } + \sqrt { 27 } - 3 \sqrt { 5 } - 2 \sqrt { 12 }\).

\(- \sqrt { 5 } - \sqrt { 3 }\)

www.youtube.com/v/QtaPdVybP1g

Next, we work with radical expressions involving variables. In this section, assume all radicands containing variable expressions are nonnegative.

Example \(\PageIndex{7}\):

Simplify: \(- 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x }\).

Combine like radicals.

\(\begin{aligned} - 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x } & = \color{Cerulean}{- 9 \sqrt [ 3 ] { 5 x } + 10 \sqrt [ 3 ] { 5 x } }\color{black}{-}\color{OliveGreen}{ \sqrt [ 3 ] { 2 x }} \\ & = \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \end{aligned}\)

We cannot combine any further because the remaining radical expressions do not share the same radicand; they are not like radicals. Note: \(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \neq \sqrt [ 3 ] { 5 x - 2 x }\).

\(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x }\)

We will often find the need to subtract a radical expression with multiple terms. If this is the case, remember to apply the distributive property before combining like terms.

Example \(\PageIndex{8}\):

Simplify: \(( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } )\).

\(\begin{aligned} ( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } ) & = 5 \sqrt { x } - 4 \sqrt { y } - 4 \sqrt { x } + 7 \sqrt { y } \quad\color{Cerulean}{Distribute.} \\ & = 5 \sqrt { x } - 4 \sqrt { x } - 4 \sqrt { y } + 7 \sqrt { y } \\ & = \sqrt { x } + 3 \sqrt { y } \end{aligned}\)

\(\sqrt { x } + 3 \sqrt { y }\)

Until we simplify, it is often unclear which terms involving radicals are similar. The general steps for simplifying radical expressions are outlined in the following example.

Example \(\PageIndex{9}\):

Simplify: \(5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right)\).

Step 1 : Simplify the radical expression. In this case, distribute and then simplify each term that involves a radical.

\(\begin{array} { l } { 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right) } \\ { = 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - x \sqrt[3] { 24 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 \sqrt [ 3 ] { 3 \cdot x \cdot x ^ { 3 } } + \sqrt [ 3 ] { 8 \cdot 3 \cdot x ^ { 3 } } - x \sqrt [ 3 ] { 8 \cdot 3 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 x \sqrt [ 3 ] { 3 x } + 2 x \sqrt [ 3 ] { 3 } - 2 x \sqrt [ 3 ] { 3 x } - 4 x \sqrt [ 3 ] { 3 } } \end{array}\)

Step 2 : Combine all like radicals. Remember to add only the coefficients; the variable parts remain the same.

\(\begin{array} { l } { =\color{Cerulean}{ 5 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{+ 2 x \sqrt [ 3 ] { 3 }}\color{Cerulean}{ - 2 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{- 4 x \sqrt [ 3 ] { 3 } } }\\ { = 3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 } } \end{array}\)

Answer : \(3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 }\)

Example \(\PageIndex{10}\):

Simplify: \(2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b }\).

\(\begin{array} { l } { 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b } } \\ { = 2 a \sqrt { 25 \cdot 5 \cdot a ^ { 2 } \cdot b } - a ^ { 2 } \sqrt { 16 \cdot 5 \cdot b } + 4 \sqrt { 4 \cdot 5 \cdot \left( a ^ { 2 } \right) ^ { 2 } b } }\quad\color{Cerulean}{Factor.} \\ { = 2 a \cdot 5 \cdot a \sqrt { 5 b } - a ^ { 2 } \cdot 4 \sqrt { 5 b } + 4 \cdot 2 \cdot a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\:\color{Cerulean}{Simplify.} \\ { = 10 a ^ { 2 } \sqrt { 5 b } - 4 a ^ { 2 } \sqrt { 5 b } + 8 a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\color{Cerulean}{Combine\:like\:terms.} \\ { = 14 a ^ { 2 } \sqrt { 5 b } } \end{array}\)

\(14 a ^ { 2 } \sqrt { 5 b }\)

Exercise \(\PageIndex{2}\)

\(\sqrt [ 3 ] { 2 x ^ { 6 } y } + \sqrt [ 3 ] { x y ^ { 3 } } - \left( y \sqrt [ 3 ] { 27 x } - 2 x \sqrt [ 3 ] { 2 x ^ { 3 } y } \right)\)

\(3 x ^ { 2 } \sqrt [ 3 ] { 2 y } - 2 y \sqrt [ 3 ] { x }\)

www.youtube.com/v/oYeyj7ubc-Q

Take careful note of the differences between products and sums within a radical. Assume both \(x\) and \(y\) are nonnegative.

\(\begin{array} { l } Products \quad \quad\quad\quad Sums\\\hline { \sqrt { x ^ { 2 } y ^ { 2 } } = x y \quad\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y } \\ { \sqrt [ 3 ] { x ^ { 3 } y ^ { 3 } } = x y } \quad\sqrt[3]{x^{3}+y^{3}} \neq x+ y \end{array}\)

The property \(\sqrt [ n ] { a \cdot b } = \sqrt [ n ] { a } \cdot \sqrt [ n ] { b }\) says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.

Example \(\PageIndex{11}\):

Calculate the perimeter of the triangle formed by the points \((-2,-1), (-3,6)\), and \((2,1)\).

The formula for the perimeter of a triangle is \(P = a + b + c\) where \(a, b\), and \(c\) represent the lengths of each side. Plotting the points we have,

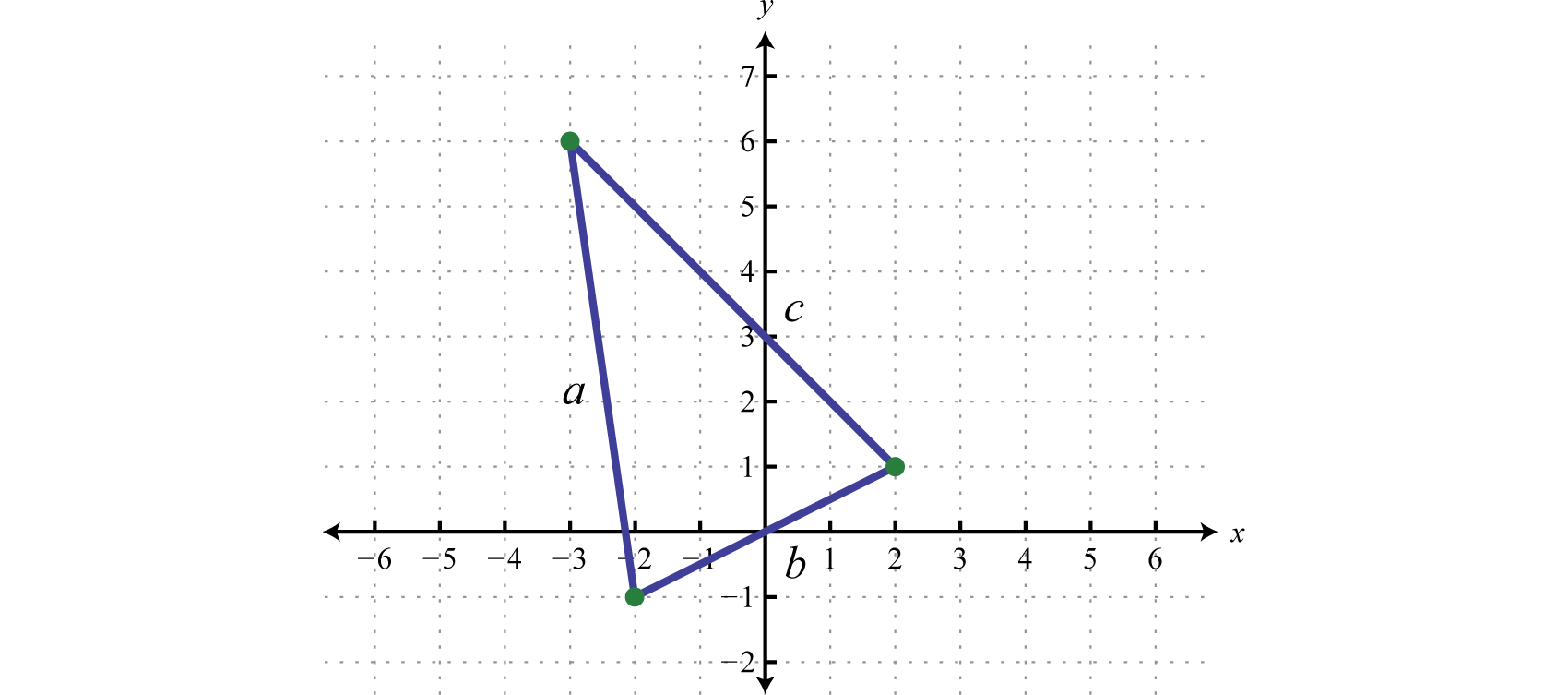
Use the distance formula to calculate the length of each side.

\(\begin{aligned} a & = \sqrt { [ - 3 - ( - 2 ) ] ^ { 2 } + [ 6 - ( - 1 ) ] ^ { 2 } } &b&= \sqrt{[2-(-2)]^{2} + [1-(-1)]^{2}} \\ & = \sqrt { ( - 3 + 2 ) ^ { 2 } + ( 6 + 1 ) ^ { 2 } } &&= \sqrt{(2+2)^{2} + (1+1)^{2}} \\ & = \sqrt { ( - 1 ) ^ { 2 } + ( 7 ) ^ { 2 } } &&=\sqrt{(4)^{2}+(2)^{2}} \\ & = \sqrt { 1 + 49 }&&= \sqrt{16+4} \\ & = \sqrt { 50 } && =\sqrt{20}\\ & = 5 \sqrt { 2 } &&= 2\sqrt{5} \end{aligned}\)

Similarly we can calculate the distance between \((−3, 6)\) and \((2,1)\) and find that \(c = 5\sqrt{2}\) units. Therefore, we can calculate the perimeter as follows:

\(\begin{aligned} P & = a + b + c \\ & = 5 \sqrt { 2 } + 2 \sqrt { 5 } + 5 \sqrt { 2 } \\ & = 10 \sqrt { 2 } + 2 \sqrt { 5 } \end{aligned}\)

\(10 \sqrt { 2 } + 2 \sqrt { 5 }\) units

Key Takeaways

• Add and subtract terms that contain like radicals just as you do like terms. If the index and radicand are exactly the same, then the radicals are similar and can be combined. This involves adding or subtracting only the coefficients; the radical part remains the same.
• Simplify each radical completely before combining like terms.

Exercise \(\PageIndex{3}\)

• \(10 \sqrt { 3 } - 5 \sqrt { 3 }\)
• \(15 \sqrt { 6 } - 8 \sqrt { 6 }\)
• \(9 \sqrt { 3 } + 5 \sqrt { 3 }\)
• \(12 \sqrt { 6 } + 3 \sqrt { 6 }\)
• \(4 \sqrt { 5 } - 7 \sqrt { 5 } - 2 \sqrt { 5 }\)
• \(3 \sqrt { 10 } - 8 \sqrt { 10 } - 2 \sqrt { 10 }\)
• \(\sqrt { 6 } - 4 \sqrt { 6 } + 2 \sqrt { 6 }\)
• \(5 \sqrt { 10 } - 15 \sqrt { 10 } - 2 \sqrt { 10 }\)
• \(13 \sqrt { 7 } - 6 \sqrt { 2 } - 5 \sqrt { 7 } + 5 \sqrt { 2 }\)
• \(10 \sqrt { 13 } - 12 \sqrt { 15 } + 5 \sqrt { 13 } - 18 \sqrt { 15 }\)
• \(6 \sqrt { 5 } - ( 4 \sqrt { 3 } - 3 \sqrt { 5 } )\)
• \(- 12 \sqrt { 2 } - ( 6 \sqrt { 6 } + \sqrt { 2 } )\)
• \(( 2 \sqrt { 5 } - 3 \sqrt { 10 } ) - ( \sqrt { 10 } + 3 \sqrt { 5 } )\)
• \(( - 8 \sqrt { 3 } + 6 \sqrt { 15 } ) - ( \sqrt { 3 } - \sqrt { 15 } )\)
• \(4 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 6 }\)
• \(\sqrt [ 3 ] { 10 } + 5 \sqrt [ 3 ] { 10 } - 4 \sqrt [ 3 ] { 10 }\)
• \(( 7 \sqrt [ 3 ] { 9 } - 4 \sqrt [ 3 ] { 3 } ) - ( \sqrt [ 3 ] { 9 } - 3 \sqrt [ 3 ] { 3 } )\)
• \(( - 8 \sqrt [ 3 ] { 5 } + \sqrt [ 3 ] { 25 } ) - ( 2 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 25 } )\)

1. \(5 \sqrt { 3 }\)

3. \(14 \sqrt { 3 }\)

5. \(- 5 \sqrt { 5 }\)

7. \(- \sqrt { 6 }\)

9. \(8 \sqrt { 7 } - \sqrt { 2 }\)

11. \(9 \sqrt { 5 } - 4 \sqrt { 3 }\)

13. \(- \sqrt { 5 } - 4 \sqrt { 10 }\)

15. \(10 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 }\)

17. \(6 \sqrt [ 3 ] { 9 } - \sqrt [ 3 ] { 3 }\)

Exercise \(\PageIndex{4}\)

Simplify. (Assume all radicands containing variable expressions are positive.)

• \(\sqrt { 2 x } - 4 \sqrt { 2 x }\)
• \(5 \sqrt { 3 y } - 6 \sqrt { 3 y }\)
• \(9 \sqrt { x } + 7 \sqrt { x }\)
• \(- 8 \sqrt { y } + 4 \sqrt { y }\)
• \(7 x \sqrt { y } - 3 x \sqrt { y } + x \sqrt { y }\)
• \(10 y ^ { 2 } \sqrt { x } - 12 y ^ { 2 } \sqrt { x } - 2 y ^ { 2 } \sqrt { x }\)
• \(2 \sqrt { a b } - 5 \sqrt { a } + 6 \sqrt { a b } - 10 \sqrt { a }\)
• \(- 3 x \sqrt { y } + 6 \sqrt { y } - 4 x \sqrt { y } - 7 \sqrt { y }\)
• \(5 \sqrt { x y } - ( 3 \sqrt { x y } - 7 \sqrt { x y } )\)
• \(- 8 a \sqrt { b } - ( 2 a \sqrt { b } - 4 \sqrt { a b } )\)
• \(( 3 \sqrt { 2 x } - \sqrt { 3 x } ) - ( \sqrt { 2 x } - 7 \sqrt { 3 x } )\)
• \(( \sqrt { y } - 4 \sqrt { 2 y } ) - ( \sqrt { y } - 5 \sqrt { 2 y } )\)
• \(5 \sqrt [ 3 ] { x } - 12 \sqrt [ 3 ] { x }\)
• \(- 2 \sqrt [ 3 ] { y } - 3 \sqrt [ 3 ] { y }\)
• \(a \sqrt [ 5 ] { 3 b } + 4 a \sqrt [ 5 ] { 3 b } - a \sqrt [ 5 ] { 3 b }\)
• \(- 8 \sqrt [ 4 ] { a b } + 3 \sqrt [ 4 ] { a b } - 2 \sqrt [ 4 ] { a b }\)
• \(6 \sqrt { 2 a } - 4 \sqrt [ 3 ] { 2 a } + 7 \sqrt { 2 a } - \sqrt [ 3 ] { 2 a }\)
• \(4 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a } - 9 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a }\)
• \(( \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } ) - ( 2 \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } )\)
• \(( 5 \sqrt [ 5 ] { 6 y } - 5 \sqrt { y } ) - ( 2 \sqrt [ 6 ] { 6 y } + 3 \sqrt { y } )\)
• \(2 x ^ { 2 } \sqrt [ 3 ] { 3 x } - \left( x ^ { 2 } \sqrt [ 3 ] { 3 x } - x \sqrt [ 3 ] { 3 x } \right)\)
• \(5 y ^ { 3 } \sqrt { 6 y } - \left( \sqrt { 6 y } - 4 y ^ { 3 } \sqrt { 6 y } \right)\)

1. \(- 3 \sqrt { 2 x }\)

3. \(16 \sqrt { x }\)

5. \(5 x \sqrt { y }\)

7. \(8 \sqrt { a b } - 15 \sqrt { a }\)

9. \(9 \sqrt { x y }\)

11. \(2 \sqrt { 2 x } + 6 \sqrt { 3 x }\)

13. \(- 7 \sqrt [ 3 ] { x }\)

15. \(4 a \sqrt [ 5 ] { 3 b }\)

17. \(13 \sqrt { 2 a } - 5 \sqrt [ 3 ] { 2 a }\)

19. \(- \sqrt [ 4 ] { 4 x y }\)

21. \(x ^ { 2 } \sqrt [ 3 ] { 3 x } + x \sqrt [ 3 ] { 3 x }\)

Exercise \(\PageIndex{5}\)

• \(\sqrt { 75 } - \sqrt { 12 }\)
• \(\sqrt { 24 } - \sqrt { 54 }\)
• \(\sqrt { 32 } + \sqrt { 27 } - \sqrt { 8 }\)
• \(\sqrt { 20 } + \sqrt { 48 } - \sqrt { 45 }\)
• \(\sqrt { 28 } - \sqrt { 27 } + \sqrt { 63 } - \sqrt { 12 }\)
• \(\sqrt { 90 } + \sqrt { 24 } - \sqrt { 40 } - \sqrt { 54 }\)
• \(\sqrt { 45 } - \sqrt { 80 } + \sqrt { 245 } - \sqrt { 5 }\)
• \(\sqrt { 108 } + \sqrt { 48 } - \sqrt { 75 } - \sqrt { 3 }\)
• \(4 \sqrt { 2 } - ( \sqrt { 27 } - \sqrt { 72 } )\)
• \(- 3 \sqrt { 5 } - ( \sqrt { 20 } - \sqrt { 50 } )\)
• \(\sqrt [ 3 ] { 16 } - \sqrt [ 3 ] { 54 }\)
• \(\sqrt [ 3 ] { 81 } - \sqrt [ 3 ] { 24 }\)
• \(\sqrt [ 3 ] { 135 } + \sqrt [ 3 ] { 40 } - \sqrt [ 3 ] { 5 }\)
• \(\sqrt [ 3 ] { 108 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 4 }\)
• \(2 \sqrt { 27 } - 2 \sqrt { 12 }\)
• \(3 \sqrt { 50 } - 4 \sqrt { 32 }\)
• \(3 \sqrt { 243 } - 2 \sqrt { 18 } - \sqrt { 48 }\)
• \(6 \sqrt { 216 } - 2 \sqrt { 24 } - 2 \sqrt { 96 }\)
• \(2 \sqrt { 18 } - 3 \sqrt { 75 } - 2 \sqrt { 98 } + 4 \sqrt { 48 }\)
• \(2 \sqrt { 45 } - \sqrt { 12 } + 2 \sqrt { 20 } - \sqrt { 108 }\)
• \(( 2 \sqrt { 363 } - 3 \sqrt { 96 } ) - ( 7 \sqrt { 12 } - 2 \sqrt { 54 } )\)
• \(( 2 \sqrt { 288 } + 3 \sqrt { 360 } ) - ( 2 \sqrt { 72 } - 7 \sqrt { 40 } )\)
• \(3 \sqrt [ 3 ] { 54 } + 5 \sqrt [ 3 ] { 250 } - 4 \sqrt [ 3 ] { 16 }\)
• \(4 \sqrt [ 3 ] { 162 } - 2 \sqrt [ 3 ] { 384 } - 3 \sqrt [ 3 ] { 750 }\)

1. \(3 \sqrt { 3 }\)

3. \(2 \sqrt { 2 } + 3 \sqrt { 3 }\)

5. \(5 \sqrt { 7 } - 5 \sqrt { 3 }\)

7. \(5 \sqrt { 5 }\)

9. \(10 \sqrt { 2 } - 3 \sqrt { 3 }\)

11. \(- \sqrt [ 3 ] { 2 }\)

13. \(4 \sqrt [ 3 ] { 5 }\)

15. \(2 \sqrt { 3 }\)

17. \(23 \sqrt { 3 } - 6 \sqrt { 2 }\)

19. \(- 8 \sqrt { 2 } + \sqrt { 3 }\)

21. \(8 \sqrt { 3 } - 6 \sqrt { 6 }\)

23. \(26 \sqrt[3] { 2 }\)

Exercise \(\PageIndex{6}\)

• \(\sqrt { 81 b } + \sqrt { 4 b }\)
• \(\sqrt { 100 a } + \sqrt { a }\)
• \(\sqrt { 9 a ^ { 2 } b } - \sqrt { 36 a ^ { 2 } b }\)
• \(\sqrt { 50 a ^ { 2 } } - \sqrt { 18 a ^ { 2 } }\)
• \(\sqrt { 49 x } - \sqrt { 9 y } + \sqrt { x } - \sqrt { 4 y }\)
• \(\sqrt { 9 x } + \sqrt { 64 y } - \sqrt { 25 x } - \sqrt { y }\)
• \(7 \sqrt { 8 x } - ( 3 \sqrt { 16 y } - 2 \sqrt { 18 x } )\)
• \(2 \sqrt { 64 y } - ( 3 \sqrt { 32 y } - \sqrt { 81 y } )\)
• \(2 \sqrt { 9 m ^ { 2 } n } - 5 m \sqrt { 9 n } + \sqrt { m ^ { 2 } n }\)
• \(4 \sqrt { 18 n ^ { 2 } m } - 2 n \sqrt { 8 m } + n \sqrt { 2 m }\)
• \(\sqrt { 4 x ^ { 2 } y } - \sqrt { 9 x y ^ { 2 } } - \sqrt { 16 x ^ { 2 } y } + \sqrt { y ^ { 2 } x }\)
• \(\sqrt { 32 x ^ { 2 } y ^ { 2 } } + \sqrt { 12 x ^ { 2 } y } - \sqrt { 18 x ^ { 2 } y ^ { 2 } } - \sqrt { 27 x ^ { 2 } y }\)
• \(\left( \sqrt { 9 x ^ { 2 } y } - \sqrt { 16 y } \right) - \left( \sqrt { 49 x ^ { 2 } y } - 4 \sqrt { y } \right)\)
• \(\left( \sqrt { 72 x ^ { 2 } y ^ { 2 } } - \sqrt { 18 x ^ { 2 } y } \right) - \left( \sqrt { 50 x ^ { 2 } y ^ { 2 } } + x \sqrt { 2 y } \right)\)
• \(\sqrt { 12 m ^ { 4 } n } - m \sqrt { 75 m ^ { 2 } n } + 2 \sqrt { 27 m ^ { 4 } n }\)
• \(5 n \sqrt { 27 m n ^ { 2 } } + 2 \sqrt { 12 m n ^ { 4 } } - n \sqrt { 3 m n ^ { 2 } }\)
• \(2 \sqrt { 27 a ^ { 3 } b } - a \sqrt { 48 a b } - a \sqrt { 144 a ^ { 3 } b }\)
• \(2 \sqrt { 98 a ^ { 4 } b } - 2 a \sqrt { 162 a ^ { 2 } b } + a \sqrt { 200 b }\)
• \(\sqrt [ 3 ] { 125 a } - \sqrt [ 3 ] { 27 a }\)
• \(\sqrt [ 3 ] { 1000 a ^ { 2 } } - \sqrt [ 3 ] { 64 a ^ { 2 } }\)
• \(2 x \sqrt [ 3 ] { 54 x } - 2 \sqrt [ 3 ] { 16 x ^ { 4 } } + 5 \sqrt [ 3 ] { 2 x ^ { 4 } }\)
• \(x \sqrt [ 3 ] { 54 x ^ { 3 } } - \sqrt [ 3 ] { 250 x ^ { 6 } } + x ^ { 2 } \sqrt [ 3 ] { 2 }\)
• \(\sqrt [ 4 ] { 16 y ^ { 2 } } + \sqrt [ 4 ] { 81 y ^ { 2 } }\)
• \(\sqrt [ 5 ] { 32 y ^ { 4 } } - \sqrt [ 5 ] { y ^ { 4 } }\)
• \(\sqrt [ 4 ] { 32 a ^ { 3 } } - \sqrt [ 4 ] { 162 a ^ { 3 } } + 5 \sqrt [ 4 ] { 2 a ^ { 3 } }\)
• \(\sqrt [ 4 ] { 80 a ^ { 4 } b } + \sqrt [ 4 ] { 5 a ^ { 4 } b } - a \sqrt [ 4 ] { 5 b }\)
• \(\sqrt [ 3 ] { 27 x ^ { 3 } } + \sqrt [ 3 ] { 8 x } - \sqrt [ 3 ] { 125 x ^ { 3 } }\)
• \(\sqrt [ 3 ] { 24 x } - \sqrt [ 3 ] { 128 x } - \sqrt [ 3 ] { 81 x }\)
• \(\sqrt [ 3 ] { 27 x ^ { 4 } y } - \sqrt [ 3 ] { 8 x y ^ { 3 } } + x \sqrt [ 3 ] { 64 x y } - y \sqrt [ 3 ] { x }\)
• \(\sqrt [ 3 ] { 125 x y ^ { 3 } } + \sqrt [ 3 ] { 8 x ^ { 3 } y } - \sqrt [ 3 ] { 216 x y ^ { 3 } } + 10 x ^ { 3 } \sqrt { y }\)
• \(\left( \sqrt [ 3 ] { 162 x ^ { 4 } y } - \sqrt [ 3 ] { 250 x ^ { 4 } y ^ { 2 } } \right) - \left( \sqrt [ 3 ] { 2 x ^ { 4 } y ^ { 2 } } - \sqrt [ 3 ] { 384 x ^ { 4 } y } \right)\)
• \(\left( \sqrt [ 5 ] { 32 x ^ { 2 } y ^ { 6 } } - \sqrt [ 5 ] { 243 x ^ { 6 } y ^ { 2 } } \right) - \left( \sqrt [ 5 ] { x ^ { 2 } y ^ { 6 } } - x \sqrt [ 5 ] { x y ^ { 2 } } \right)\)

1. \(11 \sqrt { b }\)

3. \(- 3 a \sqrt { b }\)

5. \(8 \sqrt { x } - 5 \sqrt { y }\)

7. \(20 \sqrt { 2 x } - 12 \sqrt { y }\)

9. \(- 8 m \sqrt { n }\)

11. \(- 2 x \sqrt { y } - 2 y \sqrt { x }\)

13. \(- 4 x \sqrt { y }\)

15. \(3 m ^ { 2 } \sqrt { 3 n }\)

17. \(2 a \sqrt { 3 a b } - 12 a ^ { 2 } \sqrt { a b }\)

19. \(2 \sqrt [ 3 ] { a }\)

21. \(7 x \sqrt [ 3 ] { 2 x }\)

23. \(5 \sqrt [ 4 ] { y ^ { 2 } }\)

25. \(4 \sqrt [ 4 ] { 2 a ^ { 3 } }\)

27. \(- 2 x + 2 \sqrt [ 3 ] { x }\)

29. \(7 x \sqrt [ 3 ] { x y } - 3 y \sqrt [ 3 ] { x }\)

31. \(7 x \sqrt [ 3 ] { 6 x y } - 6 x \sqrt [ 3 ] { 2 x y ^ { 2 } }\)

Exercise \(\PageIndex{7}\)

Calculate the perimeters of the triangles formed by the following set of vertices.

• \(\{ ( - 4 , - 5 ) , ( - 4,3 ) , ( 2,3 ) \}\)
• \(\{ ( - 1,1 ) , ( 3,1 ) , ( 3 , - 2 ) \}\)
• \(\{ ( - 3,1 ) , ( - 3,5 ) , ( 1,5 ) \}\)
• \(\{ ( - 3 , - 1 ) , ( - 3,7 ) , ( 1 , - 1 ) \}\)
• \(\{ ( 0,0 ) , ( 2,4 ) , ( - 2,6 ) \}\)
• \(\{ ( - 5 , - 2 ) , ( - 3,0 ) , ( 1 , - 6 ) \}\)
• A square garden that is \(10\) feet on each side is to be fenced in. In addition, the space is to be partitioned in half using a fence along its diagonal. How much fencing is needed to do this? (Round to the nearest tenth of a foot.)
• A garden in the shape of a square has an area of \(150\) square feet. How much fencing is needed to fence it in? (Hint: The length of each side of a square is equal to the square root of the area. Round to the nearest tenth of a foot.)

1. \(24\) units

3. \(8 + 4 \sqrt { 2 }\) units

5. \(4 \sqrt { 5 } + 2 \sqrt { 10 }\) units

7. \(54.1\) feet

Exercise \(\PageIndex{8}\)

• Choose values for \(x\) and \(y\) and use a calculator to show that \(\sqrt { x + y } \neq \sqrt { x } + \sqrt { y }\).
• Choose values for \(x\) and \(y\) and use a calculator to show that \(\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y\).

1. Answer may vary

16 Radicals that share the same index and radicand.

17 Term used when referring to like radicals.