problem solving with triangles and area

Free Mathematics Tutorials

Area of Triangles Problems with Solutions

A set of problems on how to calculate the area of triangles using different formulas are presented along with detailed solutions .

Formulas for Area of Triangles

We first recall some of the most widely used formulas used to calculate the area of a triangle.

Formula 1 - Base and Height of a triangle are known

Area = (1 / 2) × base × height = (1 / 2) × AB × CD

Formula 2 - Two sides of a triangle and the angle between them are known

Formula 3 - Three sides of a triangle are known

Formula 4 - the three vertices of the triangle are known by their coordinates, problems on areas with solutions.

Problem 4 Find the area of an equilateral triangle wide length equal to 6 cm.

Problem 7 Find the area of the triangle whose vertices are the points of intersection of the lines with equations y = x , y = - x + 4 and y = 2 x + 2.

Solutions to the Above Problems

Solution to Problem 2 Triangle CDB has a base CD of length 20. Its height is the side AB of the triangle because it start from the vertex B opposite the base CD is perpendicular to AC and therefore to the base DC. Hence the use of formula 1 to find the area of triangle. Area = (1/2) × 20 × 80 = 40 unit 2

Solution to Problem 3 We are given two sides and the angle opposite one of the sides. One way to find the area is to find angle B and use formula 2. Use the sine law to write sin(A) / BC = sin(C) / AB which gives sin(A) = 6 sin(55°) / 5 A = sin -1 (6 sin(55°) / 5) = 79.4 ° We now determine angle B using that fact that the sum of all angles in a triangle to be 180 °. B = 180 - 55 - 79.4 = 45.6 ° Use formula 2 to find the area Area = (1 / 2) × 5 × 6 × sin(45.6 °) = 10.7 unit 2

Solution to Problem 8 The shape whose are is to be calculated is made up of two triangles ADC and ACB with a common side AC. The area of triangle ACB can be calculated using formula 2 (we know two sides and the angle between them). For triangle ADC ,we know two sides. We can find side AC using the cosine law . in triangle ACB as follows AC 2 = AB 2 + CB 2 - 2 (AB)(AC) cos (B) Substitute by the numerical values and calculate AC AC = √( 400 2 + 800 2 - 2 (400)(800) cos (45°) ) = 589.5 We may use Heron's formula since we know the three sides of triangle ADC Let s = (1/2)(AD + DC + CA) = (1/2)(245 + 432 + 589.5) = 633.25 Area of triangle ADC = √( s × (s - AD) × (s - DC) × (s - CA) ) = √( 633.25 × (633.25 - 245) × (633.25 - 432) × (633.25 - 589.5) ) = 46526 ft 2 Area of triangle ACB = (1 / 2) BA × BC × sin (B) = (1 / 2) 400 × 800 × sin (45°) = 113137 ft 2 Total area of the given shape is obtained by adding the areas of triangles ADC and ACB Area = 46526 + 113137 = 158663 ft 2

More References and Links

Popular pages.

• Privacy Policy

How to find the Area of a Triangle

To find the area of a triangle, use the following formula

The area of a triangle is always half the product of the height and base.

$ Area = \frac{1}{2} (base \cdot height) $

So which side is the base?

Any side of the triangle can be a base. All that matters is that the base and the height must be perpendicular.

Any side can be a base, but every base has only one height. The height is the line from the opposite vertex and perpendicular to the base. The illustration below shows how any leg of the triangle can be a base and the height always extends from the vertex of the opposite side and is perpendicular to the base. Play around with our applet to see how the area of a triangle can be computed from any base/height pairing.

The picture below shows you that the height can actually extend outside of the triangle . So technically the height does not necessarily intersect with the base.

Derivation of the Area of a Triangle from Rectangle

What is the area of the triangle pictured below?

Use the formula above.

$$ A = \frac{1}{2} (base \cdot height) \\ A = \frac{1}{2} (10 \cdot 3) \\ = \frac{1}{2} (30) \\ = \frac{30}{2} = 15 $$

Practice Problems

Find the area of each triangle below. Round each answer to the nearest tenth of a unit .

What is the area of the triangle in the following picture?

To find the area of the triangle on the left, substitute the base and the height into the formula for area .

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (3 \cdot 3) \\ = \frac{1}{2} (9) \\ =\frac{9}{2} \\ = 4.5 \text{ inches squared} $$

Calculate the area of the triangle pictured below.

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (24 \cdot 27.6) \\ = 331.2 \text{ inches squared} $$

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (12 \cdot 2.5) \\ = 15 \text{ inches squared} $$

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (12 \cdot 3.9) \\ = 23.4 \text{ inches squared} $$

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (14 \cdot 4) \\ = 28 \text{ inches squared} $$

What is the area of the following triangle?

This problems involves 1 small twist. You must decide which of the 3 bases to use . Just remember that base and height are perpendicular. Therefore, the base is '11' since it is perpendicular to the height of 13.4.

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (11 \cdot 13.4) \\ = 73.7 \text{ inches squared} $$

This problems involves 1 small twist. You must decide which of the 3 bases to use . Just remember that base and height are perpendicular. Therefore, the base is '12' since it is perpendicular to the height of 5.9.

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (12 \cdot 5.9) \\ = 35.4 \text{ inches squared} $$

Like the last problem, you must decide which of the 3 bases to use . Just remember that base and height are perpendicular. Therefore, the base is '4' since it is perpendicular to the height of 17.7.

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (4 \cdot 17.7) \\ = 35.4 \text{ inches squared} $$

Again, you must decide which of the 3 bases to use . Just remember that base and height are perpendicular. Therefore, the base is '22' since it is perpendicular to the height of 26.8.

$$ Area = \frac{1}{2} (base \cdot height) \\ =\frac{1}{2} (22 \cdot 26.8) \\ = 294.8 \text{ inches squared} $$

• Area of Triangle Home
• Heron's Formula for Area
• Area Using SAS

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Trig without Tears Part 4:

Solving Triangles

Copyright © 1997–2024 by Stan Brown, BrownMath.com

For all of this, you need only two tools, the Law of Sines and the Law of Cosines . The Law of Sines relates any two sides and the angles opposite them, and the Law of Cosines relates all three sides and one angle.

• How to Solve Triangles on TI-83/84 includes a TI-83/84 program to automate the computations mentioned in this chapter.
• There’s an online triangle solver , by Jesús SD, for checking your answers. Click through the prompt about Chrome; it seems to work fine in the other browsers that I tried.

Law of Sines

Law of cosines, special note: side-side-angle, solving triangles from area, practice problems, btw: great book on problem solving.

Let’s look at a specific example to start with. Suppose you have a triangle where one side has a length of 180, an adjacent angle is 42°, and the opposite angle is 31°. You’re asked to find the other angle and the other two sides.

We’ve already got the diagram, but let’s see if those other techniques will be helpful. (By the way, they’re not original with me, but are from a terrific book on problem-solving techniques that I think you should know about.)

“Can you use what you already know to solve a piece of this problem?” For example, if this were a right triangle you’d know right away how to write down the lengths of sides in terms of sines or cosines .

But it’s not a right triangle, alas. Is there any way to turn it into a right triangle? Not exactly, but if you construct a line at right angles to one side and passing through the opposite vertex, you’ll have two right triangles. Maybe solving those right triangles will show how to solve the original triangle.

Let’s start by writing down things we know that relate the sides and angles of the two right triangles in the diagram above. You remember how to write down the lengths of the legs of a right triangle ? The leg is always equal to the hypotenuse times either the cosine of the adjacent angle or the sine of the opposite angle. (If that looks like just empty words to you, or even if you’re not 100% confident about it, please go back and review that section until you feel confident.)

AD =  b  cos  A and CD =  b  sin  A

By the same reasoning, in the other triangle you have

DB =  a  cos  B and CD =  a  sin  B

This is striking: you see two different expressions for the length CD. But things that are equal to the same thing are equal to each other. That means that

b  sin  A  = a  sin  B

Divide through by sin  A and you have the solution for the general case:

b  =  a  sin  B  / sin  A

b  = 180 × sin 42° / sin 31° ≈ 234

What about the third angle, C , and the third side, c ? Well, when you have two angles of a triangle you can find the third one easily:

A  + B  + C  = 180°

C  = 180° − A  − B

In this case, C  = 180° − 31° − 42° = 107°.

For the third side, there are a couple of ways to go. You wrote expressions above for AD and DB, and you know that c  = AD+DB, so you could compute c  =  b  cos  A  + a  cos  B .

But that’s two multiplies and an add, a bit more complicated than the one multiply and one divide to find side b . I’m lazy, and I like to reduce the amount of tapping I do on my calculator. Is there an easier way, even if just slightly easier? Yes, there is. Go back a step, to

a  sin  B = b  sin  A

Divide left and right by (sin  A )(sin  B ) to get

a /sin  A  =  b /sin  B

Because C  > 90°, this perpendicular happens to be outside the triangle and the two right triangles ABD and CBD overlap. But this won’t affect the algebra. By the way, the angle in triangle CBD is not C but 180° − C , the supplement of C . Angle C belongs to the original triangle ABC.

You can write the length of the common side BD as

BD = c  sin  A (in triangle ABD)

BD = a  sin(180° − C ) (in triangle CBD)

But sin(180° − C ) = sin  C , so you have

BD = a  sin  C (in triangle CBD)

Set the two computed lengths of BD equal to each other, and divide by (sin  A )(sin  C ):

a  sin  C  = c  sin  A

a /sin  A  = c /sin  C

But we already figured out earlier that

Combining these two equations you have the Law of Sines :

(28) Law of Sines—First Form:

a /sin  A  =  b /sin  B  =  c /sin  C

This is very simple and beautiful: for any triangle, if you divide any side by the sine of the opposite angle , you’ll get the same result. This law is valid for any triangle.

You can derive the Law of Sines at need, so I don’t specifically recommend memorizing it. But it’s so simple and beautiful that it’s pretty hard not to memorize if you use it at all. It’s also pretty hard to remember it wrong: there are no alternating plus and minus signs or combinations of different functions.

a /sin  A = c /sin  C

a (sin  C )/(sin  A ) = c

c = 180 × (sin 107°)/(sin 31°) ≈ 334

The Law of Sines is sometimes given upside down:

(29) Law of Sines—Second Form:

(sin  A )/ a  =  (sin  B )/ b  =  (sin  C )/ c

Of course that’s the same law, just as 2/3 = 6/9 and 3/2 = 9/6 are the same statement. Work with it either way, and you’ll come up with the same answers.

In most cases where you use the Law of Sines, you get a unique solution. But sometimes you get two solutions (or none) in the side-side-angle case, where you know two sides and an angle that’s not between them. Please see the Special Note below, after the table.

The Law of Sines is fine when you can relate sides and angles. But suppose you know three sides of the triangle—for instance a  = 180, b  = 238, c  = 340—and you have to find the three angles. The Law of Sines is no good for that, because it relates two sides and their opposite angles. If you don’t know any angles, you have an equation with two unknowns and you can’t solve it.

Let’s look back at that generic triangle with a perpendicular dropped from vertex C . You may remember that when we first looked at this picture, we pulled out information using both the sine and the cosine of the two angles. We used the sine information to develop the Law of Sines, but we never went anywhere with the cosine information, which was

AD = b cos  A    and    DB or BD = a cos  B

Let’s see where that can lead us. You remember that the way we came up with the Law of Sines was to write two equations that featured the length of the construction line CD, and then combine the equations to eliminate CD. Can we do anything like that here?

Well, we know the other two sides of those right triangles, so we can write an expression for the height CD using the Pythagorean theorem—actually, two expressions, one for each triangle.

a ² = (CD)² + (BD)² ⇒ (CD)² =  a ² − (BD)²

b ² = (CD)² + (AD)² ⇒ (CD)² =  b ² − (AD)²

and therefore

a ² − (BD)² = b ² − (AD)²

Substitute the known values BD = a  cos  B and AD = b  cos  A , and you have

a ² − a ² cos²  B  =  b ² − b ² cos²  A

Bzzt! No good! That uses two sides and two angles, but we need an equation in three sides and one angle, so that we can solve for that angle. Let’s back up a step, to a ² − (BD)² =  b ² − (AD)², and see if we can go in a different direction.

Maybe the problem is in treating BD and AD as separate entities when actually they’re parts of the same line. Since BD + AD =  c , we can write

BD = c  − AD

BD = c  − b  cos  A .

Notice that this brings in the third side, c , and angle B drops out. Substituting, we now have

a ² − ( c − b  cos  A )² = b ² − ( b  cos  A )²

This looks worse than the other one, but actually it’s better because it’s what we’re looking for: an equation for the three sides and one angle. We can solve it with a little algebra:

a ² − c ² + 2 b c cos  A − b ²cos² A = b ² − b ²cos² A

a ² − c ² + 2 b c cos  A = b ²

2 b c cos  A = b ² + c ² − a ²

cos  A = ( b ² + c ² − a ²) / 2 b c

cos  A = (238² + 340² − 180²) / (2 × 238 × 340)

cos  A ≈ 0.864088

A ≈ 30.2°

Do the same thing to find the second angle (or use the Law of Sines, since it’s less work), then subtract the two known angles from 180° to find the third angle.

You can find the Law of Cosines for the other angles by following the same process using the other two perpendiculars.

(30) Law of Cosines—First Form:

cos  B = ( a ² + c ² − b ²) / 2 a c

cos  C = ( a ² + b ² − c ²) / 2 a b

cos  C = (180² + 238² − 340²) / (2 × 180 × 238)

cos  C ≈ −0.309944

C ≈ 108.1°

Notice that the Law of Cosines automatically handles acute and obtuse angles. Remember from the diagram in Functions of Any Angle that cos  A is negative when A is between 90° and 180°. Because the cosine has unique values all the way from 0° to 180°, you never have to worry about multiple solutions of a triangle when you use the Law of Cosines.

There’s another well-known form of the Law of Cosines, which may be a bit easier to remember. Start with the above form, multiply through by 2 a b , and isolate c on one side:

2 a b  cos  C = a ² + b ² − c ²

c ² = a ² + b ² − 2 a b  cos  C

You can play the same game to solve for the other two sides:

(31) Law of Cosines—Second Form:

a ² = b ² + c ² − 2 b c  × cos  A

b ² = a ² + c ² − 2 a c  × cos  B

c ² = a ² + b ² − 2 a b  × cos  C

Typically you’ll use the Law of Cosines in the first form for finding an angle and the second form for finding a side .

Probably you don’t want to try to remember that, but it’s not as hard as it looks. I think of it this way: the square of one side is the sum of the squares of the other two, like Pythagoras, but with a “correction factor” of 2 times those same sides times the cosine of the opposite angle.

Detective Work: Solving All Types of Triangles

With just the definitions of sine, cosine, and tangent , you can solve any right triangle . If you’ve got the Law of Sines and the Law of Cosines under your belt, you can solve any triangle that exists . (Some sets of givens lead to an impossible situation, like a “triangle” with sides 3-4-9.)

Really, it’s pretty straightforward. Whenever you have to solve a triangle, think about what you have and then think about which formula you can use to get what you need. (When you have two angles, you can always find the third by A  + B  + C  = 180°.)

Many people find it easier to think about the known elements of a triangle as a “case”. For instance, if you know two angles and the side between them, that’s case ASA; if you know two angles and a side that’s not between them, that’s case AAS, and so on.

I’m not presenting the following table for you to memorize. Instead, what I hope to do is show you that between the Law of Sines and the Law of Cosines you can solve any triangle, and that you simply pick which law to use based on which one has just one unknown and otherwise uses information you already have.

Most cases can be solved with the Law of Sines. But if you have three sides ( SSS ), or two sides and the angle between them ( SAS ), you must begin with the Law of Cosines.

Suppose you know acute angle B and sides a and b . Given those facts, there are two different ways you could draw the triangle, as shown in the picture. How can this be? Well, you use the Law of Sines to find angle A . Let’s say you find sin  A  = 0.95. That means A could be either about 72° or the supplement, about 108° . Remember that the sine of any angle and the sine of its supplement are the same.

This is the infamous ambiguous case . You can see the problem from the picture: the known opposite side b can take either of two positions that satisfy the given the lengths of a and b . Those two positions give rise to two different values for angle A , two different values for angle C , and two different values for side c . Think about it for a while, maybe sketch some pictures, and you’ll see that this ambiguity can arise only when the known angle is acute, and the adjacent side is longer than the opposite side, and the opposite side is greater than the height.

(Once you know the size or sizes of angle A , you can find angle C by subtracting 180° − B  − A .)

Here’s a complete rundown of all the possibilities with the SSA case:

For heaven’s sake, don’t try to memorize that table! Instead, always draw a picture. If you can draw two pictures that both fit all the available facts, you have two legitimate solutions. If only one picture fits all the facts, it will show you which angle (if any) is > 90°. And if you can’t make any picture that fits the facts, the triangle has no solution.

If you do have two solutions, what do you do? If you have no other information to go on, of course you report both solutions. But check the situation carefully. Maybe you’re told explicitly which is the largest angle, or it’s implied by other facts you know. In that case your solution is constrained, and you reject the solution that doesn’t meet the constraints.

Example: Suppose you are asked to solve a triangle with B  = 36.9° a  = 75.3, and b  = 51.3. How do you proceed?

This is the side-side-angle case: you know two sides a and b , and a non-included angle B . The adjacent side to angle B , a  = 75.3, is larger than the opposite side, b  = 51.3, so you have to compute the height, h = 75.3 sin 36.9° ≈ 45.2. The opposite side, b  = 51.3, is larger than this, so there are two solutions.

Use the Law of Sines, equation 29 , to get the second angle:

(sin  A )/ a = (sin  B )/ b

sin  A = ( a / b ) sin  B

sin  A = (75.3 / 51.3) sin 36.9° ≈ 0.8813

A = 61.8° or 180° − 61.8° = 118.2°

Given: Area and Two Angles

In April 2016, Caroline McKnoe asked me how to solve a triangle if you have two angles and the area . I hadn’t run across that one before, but it’s doable with the standard ploy of dropping a perpendicular.

area = ( c b sin  A )/2

We know angle A —even if A isn’t one of the two givens we can easily find it by subtracting the other two from 180°—but there are two unknown sides in that equation. How can we eliminate one of them? We need some second equation that involves b and c but no other unknowns. The answer is in the Law of Sines :

b /sin  B  = c /sin  C ⇒ b  = c  sin  B /sin  C

Substitute that in the equation for area:

area = ( c ² sin  B  sin  A )/(2 sin  C )

Solve for side c :

c ² = 2 area sin  C /(sin  A  sin  B )

(32) c = √ 2 × area × sin  C /(sin  A  sin  B )

Finally, use the Law of Sines to find sides a and b .

Given: Area and Two Sides

In the previous section, we found a formula for area in terms of two sides and the included angle:

We couldn’t use that directly when we knew two angles and the area, but if we know two sides and the area then this formula is exactly what we want. Just solve for sin  A :

(33) sin  A = 2 × area/( b c )

Next, use the Law of Cosines to find side a . Finally, use the Law of Sines or Law of Cosines to find a second angle, and subtract those angles from 180° to find the third angle.

To get the most benefit from these problems, work them without first looking at the solutions. Refer back to the chapter text if you need to refresh your memory.

Recommendation : Work them on paper — it’s harder to fool yourself about whether you really understand a problem completely.

You’ll find full solutions for all problems . Don’t just check your answers, but check your method too.

How long must the monorail and the foot bridge be?

Bonus question: If the river has the same width all along the stretch from A to B , how wide is it?

You’re now driving along a straight side road. At the end of 9.8 miles on the side road, you turn 135° to the right, on a third road. (If you’re visualizing this from above, the 135° change of direction corresponds to an angle of 180° − 135° = 45° in the triangle.)

Assuming that road continues in the same direction, how far must you drive to reach your starting point?

I have to recommend a terrific little book, How To Solve It by G. Polya. Most teachers aren’t very good at teaching you how to solve problems and do proofs. They show you how they do them, and expect you to pick up their techniques by a sort of osmosis. But most of them aren’t very good at explaining the thought process that goes into doing a geometrical proof, or solving a dreaded “story problem”.

Polya’s book does a great job of teaching you how to solve problems. He shows you the kinds of questions you should ask yourself when you see a problem. In other words, he teaches you how to get yourself over the hum, past the floundering that most people do when they see an unfamiliar problem. And he does it with lots of examples, so that you can develop confidence in your techniques and compare your methods with his. The techniques I’ve mentioned above are just three out of the many in his book.

There’s even a handy checklist of questions you can ask yourself whenever you’re stuck on a problem.

How To Solve It was first published in 1945, and it’s periodically in and out of print. If you can’t get it from your bookstore, go to the library and borrow a copy. You won’t be sorry.

My thanks also to Alex for pointing out in the SSA example where I twice wrote side a where I meant b .

• 19 Nov 2021 : Updated a link here .
• 19 Feb 1997 : New document.

next:  5/Functions of Any Angle

Updates and new info: https://BrownMath.com/twt/

Site Map | Searches | Home Page | Contact

Reset password New user? Sign up

Existing user? Log in

Solving Triangles

Already have an account? Log in here.

To solve problems on this page, you should be familiar with the following: Sine Rule \[ \frac a{\sin(A) } = \frac b{\sin(B)} = \frac c{\sin(C) } \] Cosine Rule \[ a^2=b^2+c^2-2bc\cos(A) \\ b^2 = a^2+c^2-2ac\cos(B) \\ c^2= a^2+b^2-2ab\cos(C) \] Area of Triangle \[\text{Area} = \frac12 bc \sin(A)= \frac12 ac \sin(B) = \frac12 ab \sin(C) \]

Problem Solving - Basic

Problem solving - intermediate, problem solving - advanced.

When we want to solve a triangle, this means that we want to find all/some of the unknown lengths and angles of the triangle.

A triangle \(ABC\) has side lengths \(a = 4\) and \(b= 9,\) and \(C = \cos^{-1} \left(\frac47\right) \). What is the length of the third side, \(c?\) By the cosine rule, we have \(c^2 = a^2 + b^2 - 2ab \cos(C) \). Substituting all the relevant information, we have \(c^2 = \frac{391}7 \). Since \(c\) represents a side length of a triangle, \(c> 0 \) only, so \(c = \sqrt{ \frac{391}7} \approx 7.474\). \(_\square\)

If the area of a triangle is given to be 20 unit squared with two of its side lengths being 7 and 8, what is the sine of the angle in between these two side lengths? Using the area formula, \(\text{Area} = \frac12 bc \sin(A)\implies 20 = \frac12 \cdot 7 \cdot 8 \sin(A). \) Solving for the sine of the angle gives \( \frac57.\ _\square \)

The diagram to the right shows a triangle \(ABC\) inscribed in a \(6\times 8\) rectangle.

What is the area of this triangle?

See Part 2 and Part 3.

If the angles of a triangle are in the ratio \(4:1:1,\) then the ratio of the longest side to the perimeter is \(\text{__________}.\)

The area of an acute triangle is 10, and two side lengths of the triangle are 6 and 7. What is the cosine of the angle in between these two sides? Let the angle between the two sides be \(A.\) Then the area of the triangle is \(10 =\frac12\times 6 \times 7 \times \sin(A), \) which gives \(\sin(A) = \frac{10}{21}.\) By applying the Pythagorean identity, \( \sin^2(A) + \cos^2(A) = 1,\) so \(\cos(A) = \sqrt{1- \left(\frac{10}{21}\right)^2} = \frac{\sqrt{341}}{21}.\) \(_\square\) Note that we are only taking the positive root because the cosine of an acute angle is strictly positive.

The numerical value of the area of a triangle is given to be \( \frac{\sqrt[3]{1234}}2 \). What is the relationship between the product of the sides of the triangle to the product of sines of the angles of the triangle? Let \(D\) denote the area of the triangle, then \(\frac{\sqrt[3]{1234}}2 = D = \frac12 ab \sin(C) = \frac12 ac \sin(B) = \frac12 bc \sin(A) \). Then, \[ D^3 = \frac{1234}8 = \frac18 (abc)^2 \sin(A) \sin(B) \sin(C). \] So the relationship in question is simply \( \frac{1234}{(abc)^2} = \sin(A) \sin(B) \sin(C).\ _\square\)

A semi-circle is inscribed within an equilateral triangle such that the diameter of the semi-circle is centered on one side of the triangle and the arc is tangent to the other two sides.

If each side of the triangle is of length 4 cm, then what is the diameter of the semi-circle (in cm)?

Give your answer to 3 decimal places.

Triangle \(ABC\) has sides of length 24, 35, and 53.

Triangle \(DEF\) has side lengths equal to the lengths of the three medians of triangle \( ABC\).

Find the area of triangle \( DEF.\)

If \( AP = AC + 2\cdot CB \), what is the measure \(\angle ABP \) in degrees?

In triangle \( ABC \), \( \cos A : \cos B : \cos C = 2 : 9 : 12 \).

If \( \sin A : \sin B : \sin C = p : q : r \), where \( p \), \( q \) and \( r \) are coprime positive integers, find \( pqr-(p+q+r) \).

In \(\triangle ABC, \) if

\[a^4 + b^4 + c^4 = 2c^2\big(a^2 +b^2\big), \]

then the possible measure(s) of \(\angle C\) could be \(\text{__________}.\)

\(\) Details and Assumptions:

\(a,b,c\) are the sides of \(\triangle ABC\) opposite to \(\angle A , \angle B, \angle C\) respectively.

\(\angle C\) is measured in radians .

Triangle \(ABC\) has \(AC=BC\) and \( \angle ACB = 96^\circ \).

\(D\) is a point in \(ABC\) such that \( \angle DAB = 18^\circ\) and \(\angle DBA = 30^\circ \).

What is the measure (in degrees) of \( \angle ACD?\)

Problem Loading...

Note Loading...

Set Loading...

Area of a Triangle Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Solving Triangles

"Solving" means finding missing sides and angles.

Six Different Types

If you need to solve a triangle right now choose one of the six options below:

Which Sides or Angles do you know already? (Click on the image or link)

... or read on to find out how you can become an expert triangle solver :

Your Solving Toolbox

Want to learn to solve triangles?

Imagine you are " The Solver " ... ... the one they ask for when a triangle needs solving!

In your solving toolbox (along with your pen, paper and calculator) you have these 3 equations:

1. Angles Add to 180° :

A + B + C = 180°

When you know two angles you can find the third.

2. Law of Sines (the Sine Rule):

When there is an angle opposite a side, this equation comes to the rescue.

Note: angle A is opposite side a, B is opposite b, and C is opposite c.

3. Law of Cosines (the Cosine Rule):

This is the hardest to use (and remember) but it is sometimes needed to get you out of difficult situations.

It is an enhanced version of the Pythagoras Theorem that works on any triangle.

Six Different Types (More Detail)

There are SIX different types of puzzles you may need to solve. Get familiar with them:

This means we are given all three angles of a triangle, but no sides.

AAA triangles are impossible to solve further since there are is nothing to show us size ... we know the shape but not how big it is.

We need to know at least one side to go further. See Solving "AAA" Triangles .

This mean we are given two angles of a triangle and one side, which is not the side adjacent to the two given angles.

Such a triangle can be solved by using Angles of a Triangle to find the other angle, and The Law of Sines to find each of the other two sides. See Solving "AAS" Triangles .

This means we are given two angles of a triangle and one side, which is the side adjacent to the two given angles.

In this case we find the third angle by using Angles of a Triangle , then use The Law of Sines to find each of the other two sides. See Solving "ASA" Triangles .

This means we are given two sides and the included angle.

For this type of triangle, we must use The Law of Cosines first to calculate the third side of the triangle; then we can use The Law of Sines to find one of the other two angles, and finally use Angles of a Triangle to find the last angle. See Solving "SAS" Triangles .

This means we are given two sides and one angle that is not the included angle.

In this case, use The Law of Sines first to find either one of the other two angles, then use Angles of a Triangle to find the third angle, then The Law of Sines again to find the final side. See Solving "SSA" Triangles .

This means we are given all three sides of a triangle, but no angles.

In this case, we have no choice. We must use The Law of Cosines first to find any one of the three angles, then we can use The Law of Sines (or use The Law of Cosines again) to find a second angle, and finally Angles of a Triangle to find the third angle. See Solving "SSS" Triangles .

Tips to Solving

Here is some simple advice:

When the triangle has a right angle, then use it, that is usually much simpler.

When two angles are known, work out the third using Angles of a Triangle Add to 180° .

Try The Law of Sines before the The Law of Cosines as it is easier to use.

Word Problems - Area of Triangles

These lessons, with videos, examples, step-by-step solutions and worksheets, help Algebra students learn how to solve word problems that involve area of triangles.

Related Pages Area Of Triangles - Formulas Types Of Triangles More Lessons for Grade 9 More Geometry Lessons Math Worksheets

Writing quadratic equations to solve word problems: Area of a triangle

Example: The height of a triangle is 3 cm more than the base. The area of the triangle is 17 cm 2 . Find the base to the nearest hundredth of a cm.

How to solve a triangle if you know the area? This is a word problem you solve by writing an equation and factoring. Word Problem: Area of a Triangle

Example: The height of a triangle is 4 inches more than twice the length of the base. The area of the triangle is 35 square inches. Find the height of the triangle.

Area of a Triangle - Algebra and Geometry Help

Example: The base of triangle is 5 units less than twice the height. If the area is 75 square units, then what is the length of the base and the height?

Algebra and Triangles : solving equations linked to perimeter and area

Example: The sides of a triangle are given as 3x, x - 1 and 3x + 1. If the perimeter is 56m, find the area.

Find area of a triangle- word problem

Example: In triangle ABC, AD = 10cm, the length of CD is half the length of AD, and the length of BD is twice the length of AD. What is the area of triangle ABC?

How to find the dimensions of a triangle given its area? This problem would involving solving quadratic equations.

Example: The height of a triangle is 4 inches less than the length of the base. The area of the triangle is 30 in 2 . Find the height and the base.

Word problem involving area of triangle

Example: Before she goes camping, La Verne has to buy a tent pole to replace the one she lost on her last outing. If the area of the front of the tent is 22 square feet and the base of the tent has the dimensions indicated below, how tall must the pole be?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Choose Your Test

Sat / act prep online guides and tips, how to find the area of a triangle: formula and examples.

General Education

Geometry can be fun, but it can also give you a massive headache if you’re not sure what formulas to use or how to approach a problem.

Triangles especially have a lot of unique qualities and formulas you need to know, including the area of triangle formula. How can you figure out the area of a triangle? It’s not as simple as it is for rectangles — but it’s also not as difficult as you might think.

In this guide, we'll go over how to find the area of a triangle and give you sample problems and tips you can use to further sharpen your skills.

Quick Review: What Is Area?

Area is the total amount of space a 2-D shape (or flat surface) takes up . Every shape in math — that is, every square, rectangle, triangle, parallelogram, trapezoid, etc. — has an area, or a certain amount of space it occupies.

Area is determined by the lengths of particular sides of a shape and is always given in square units, which could be general units or things like feet, inches, meters, or miles.

The area of a rectangle, for example, is equal to the length multiplied by the width , or, as some might say, the base times the height:

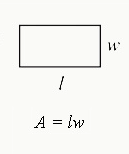
You can also simply count the number of units in the rectangle (if supplied):

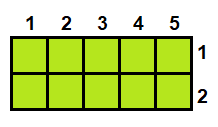
So in this example, if you counted each unit (i.e., each square) in the rectangle, you'd get 10 square units for the area of the rectangle. The other (far quicker) option for finding the area of a rectangle, however, is to multiply the length (5 units) by the width (2 units); this will also get you 10 .

This is how to find the area of a rectangle —pretty simple, really. But finding the area of a triangle is a bit trickier. For this, you’ll need to know the area of triangle formula .

Area of Triangle Formula

To find the area of a triangle, you’ll need to use the following formula:

A is the area, b is the base of the triangle (usually the bottom side), and h is the height (a straight perpendicular line drawn from the base to the highest point of the triangle). This formula may also be written like this:

Here’s a diagram to help you envision this formula at play:

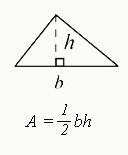
This formula works for all types of triangles:

• Equilateral: A triangle for which all three sides are equal in length

• Isosceles: A triangle for which two sides are equal in length

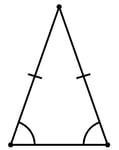
• Scalene: A triangle for which all three sides differ in length

• Right: An isosceles or scalene triangle with one right (90°) angle

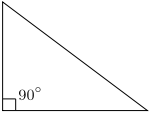
With right triangles, the base and height are simply the two sides that form the right angle . 

Now, you’re probably wondering how exactly the area of triangle formula works. It’s pretty simple actually: all triangles can be inscribed in a rectangle . This rectangle will always have double the area than that of the triangle inscribed in it.

In short, to find the area of a triangle, all you need to do is take the area of a rectangle formula ($A=bh$) and divide it by 2 .

Khan Academy has a nifty drag tool that lets you see how the area of a triangle is found using the rectangle/parallelogram it's inscribed in.

Let’s look at an example. Say that you’ve been asked to find the area of the following triangle ( not drawn to scale ):

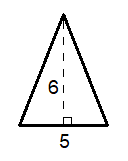
Here, we're told that the base of our triangle is 5 and the height is 6. To find the area, then, all we need to do is plug these numbers into the area formula as so:

$A=1/2bh$ $A=1/2(5)(6)$ $A=15$

This gives us an area of 15 square units for the triangle . This is a fairly straightforward example of how the area of triangle formula works. Keep reading for more sample problems!

Area of a Triangle: Sample Problems

Try your hand at finding the area of a triangle with these three sample problems. We’ll then go over the answers for each problem. Note that none of these triangles are drawn to scale .

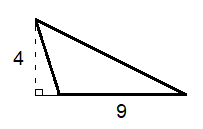
Answer Explanations

You should be able to tell right away that this is a scalene triangle , meaning that all the sides are different lengths and that there is no right angle  (unlike the triangle in #2 below).

Fortunately, you’re given all the information you need to find the area of the triangle. We are told that the base is 9 and the height is 4 (remember that the height is the line that's perpendicular to the apex, or highest point, of the triangle and the base).

Now, just plug these numbers into the area of triangle formula:

$A=1/2bh$ $A=1/2(9)(4)$ $A=18$

The area of the triangle here is 18 square units .

You should notice two things before you even attempt to solve for the area:

• It’s a right triangle , as noted by the small square in the lower-left corner
• It’s an isosceles triangle since it has two sides of equal lengths (5 and 5)

Remember that with right triangles, the base and the height are always the two sides that are not the hypotenuse . In other words, they're the two sides that connect to form a right angle. This means that, for this problem, our base is 5 and our height is also 5.

Don’t get thrown off by the square root here—that’s just extra information you don’t even need to find the area of a triangle.

Now that we know our base and height, we can simply plug these numbers into the area of a right triangle formula:

$A=1/2bh$ $A=1/2(5)(5)$ $A=12.5$

The area of this triangle is 12.5 square units .

With this problem, you likely noticed immediately that you’re not told the height of the triangle—only the lengths of the three sides ; you should also have recognized this particular triangle as an equilateral triangle , since all three sides are the same length (8 units).

So how do you approach this problem to find the area of the triangle?

In order to find the area, we need to know the base and height. Since we have the base already (8), we'll have to find the height .

Start by drawing a vertical line that dissects the triangle from its apex to the base:

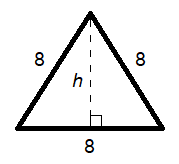
As this is an equilateral triangle, the line we drew for the height will dissect the triangle in half , thereby cutting the base in half as well. This means we'll have 4 on one side of the height line and 4 on the other:

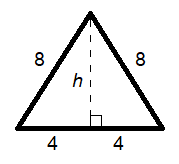
Now, look closely at this equilateral triangle. It kind of looks like two right triangles pieced together, right? That’s because it is! Thus, we can use one of these right triangles to find the length of the height line .

Let’s use the right side (it doesn’t matter which one you choose):

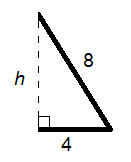
We know the length of the base (what we’ll call a ) of this right triangle, as well as the length of the hypotenuse, or c . The height, or b , is unknown, however.

So how can we use the information we have to calculate it?

This is where another formula comes into play: the Pythagorean theorem . Per the Pythagorean theorem, by squaring sides a and b (i.e., the two shorter sides) of a right triangle and then adding them together, you'll get a sum equal to the square of the hypotenuse (side c ). 

In other words:

$a^2+b^2=c^2$

As mentioned, we have a and c, so we just need to use this theorem to find b (or h in our original equilateral triangle). Here's how to do that:

$a^2+b^2=c^2$ $4^2+b^2=8^2$ $16+b^2=64$ $b^2=48$ $b=√{48}$

You can further simplify the square root by factoring out 48 like this:

$b=√{48}$ $b=√{(3*4*4)}$ $b=√{(3*4^2)}$ $b=4√3$

Now, we finally have the height of our equilateral triangle (4√3):

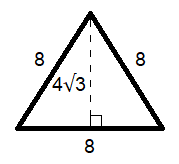
All that’s left to do is plug the base (8) and height (4√3) into our area of triangle formula:

$A=1/2bh$ $A=1/2(8)(4√3)$ $A=4(4√3)$ $A=16√3$

The area of this equilateral triangle is 16√3 square units .

How to Find the Area of a Triangle: 3 Tips

Finding the area of a triangle can be tricky, even if you know the formula. Sometimes it can be hard to understand the logic behind it or to figure out what information you need.

In this section, we give you three tips to help you find the area of a triangle with ease.

#1: Visualize a Rectangle (or Parallelogram)

It can often help to visualize the rectangle or parallelogram whose area is equal to double that of the triangle you’re analyzing.

The following diagram captures this idea nicely, indicating how if you copy the triangle and flip it, you'll get a parallelogram that equals double the area of the original triangle (since $A=bh$ for both parallelograms and rectangles):

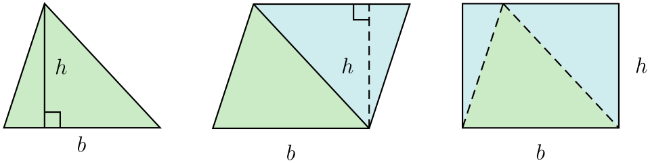
Furthermore, if you rearrange the parts of the second triangle, you can form a rectangle (instead of a parallelogram) using both the original triangle and the new one.

Once more, what this proves is that the area of a triangle will always equal half the area of the rectangle in which it is inscribed .

#2: Know How (and When) to Use the Pythagorean Theorem

Many math problems dealing with the area of a triangle aren’t just about finding the area itself but rather finding a missing side or length (typically the height), too. In these cases you'll need to know more than just how to find the area of a triangle; you'll have to know the Pythagorean theorem.

As mentioned above, the Pythagorean theorem is a formula used to find the lengths of the sides of a right triangle .

Here is the theorem once again:

In this, a is the length of one short side, b is the length of the other short side, and c is the length of the hypotenuse (that is, the longest side of a triangle). You’ll need to use the Pythagorean theorem if you’re looking for both the height and area of an isosceles or equilateral triangle.

#3: When in Doubt, Review What You’ve Learned

There’s no shame in refreshing your memory or getting help! If you’re struggling to understand how to find the area of a triangle or when and how to use the Pythagorean theorem, I strongly recommend watching some math tutorial videos .

Here’s an example of a video I found particularly helpful while writing this article:

You can also check out Khan Academy , a free website that offers a bunch of videos, lessons, and practice problems for an array of math subjects, including triangles and area .

Finally, read our SAT Math / ACT Math triangle guides to learn more about triangles in general.

What’s Next?

Got other questions about math? Our expert guides on the distributive property , PEMDAS , and SOHCAHTOA can lend you the hand you need!

Getting ready to take the SAT/ACT? Learn what's tested on SAT Math / ACT Math . You should also start memorizing the most important SAT / ACT math formulas so you can ace the Math section.

Hannah received her MA in Japanese Studies from the University of Michigan and holds a bachelor's degree from the University of Southern California. From 2013 to 2015, she taught English in Japan via the JET Program. She is passionate about education, writing, and travel.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Learn Mathematics

Area of a triangle – geometry – problems with solutions, area of a triangle.

In this lesson we will learn, how to calculate the area of a triangles with different formula’s. When given

1. The base and height of a triangle. 2. Two sides and one angle. 3. The length of three sides. 4. An equilateral triangle.

First we see about a triangle. 

A triangle is a simple closed curve, with three line segments. It has three sides three vertices and  three angles.

If we know the base, and perpendicular height of the given triangle then we can find the area of the triangle use the formula,

If we are given the base of the triangle and the perpendicular height then we can use the formula.

Area of a triangle = 1/2 x base x height

Area of triangle is equal to half of the product of its base and height. 

The height of the triangle is the perpendicular distance from vertex to the base of triangle.

Formula for area of a triangle

Area of a triangle = 1/2 x ah

Where, a is the base of the triangle and h is the height of the triangle.

We can use any three sides as a base, it depends where height is drawn.

Example 1- Find the area of a triangle with a base 4 cm and height is 3 cm.

Solution: Given that base of triangle a = 4 cm

                      and height h = 3 cm

              Area of a triangle  = 1/2 ah

= 1/2 x 4 x 3

                                      = 6 cm 2

Solution:        area of triangle = 6 cm 2

Example 2- In below figure △ ABC is inscribed inside a square of side 10 cm. Find the area of a triangle.

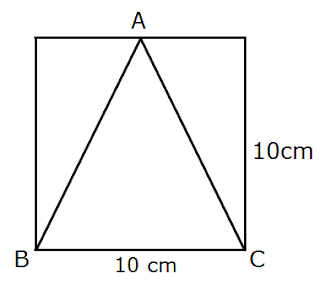
Solution: Given that  ABC is inscribed inside a square of side 10 cm.

Therefore, the height of the triangle is 10 cm and also base of the triangle is 10 cm, because △ ABC is inscribed inside a square and a square has all sides of are equal.

base of triangle a = 10 cm

                      and height h = 10 cm

       Area of a triangle  = 1/2 ah

                                 = (1/2) x 10 x 10

                area of triangle = 50 cm 2

Solution:        area of triangle = 50 cm 2

Example 3- In below figure given △ABC. Find the area of a triangle.

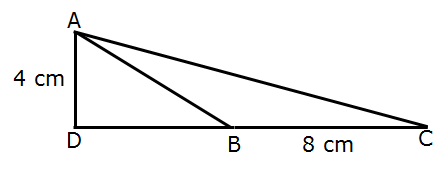
Solution: Given that base of triangle a = 8 cm

                      and height h = 4 cm

              Area of a triangle  = 1/2 ah                                        = 1/2 x 8 x 4                                        = 32/2

                                      = 16 cm 2

Solution:  area of triangle = 16 cm 2

Example 4: In below figure given △ABC. Find the area of a triangle. 

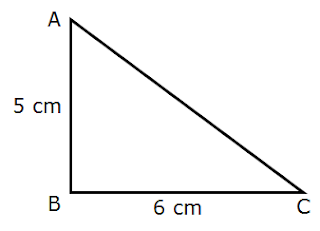
Solution: Given that  base of triangle a = 6 cm

                      and height h = 5 cm

= 1/2 x 6 x 5                                         = 30/2

                                      = 15 cm 2

Solution:   area of triangle = 15 cm 2

The length of three sides 

If given the length of three sides of a triangle, then we can use the formula to find the area of triangle.

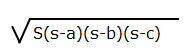
Where a, b and c are length of three sides of triangle, and S is the half of total of a, b and c.

S = (a + b + c)/2

S is the half of the perimeter.

Two sides and one angle

If given the length of two sides of a triangle and measure of a angle between them then we can use the formula to find the area of triangle.

                      Area = 1/2 ab sin C

The area of triangle is equal to half of the product of two sides times the sine of the included angle. 

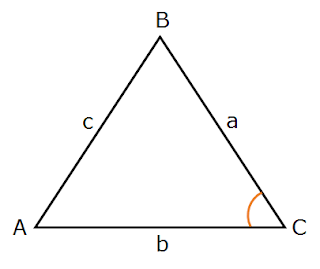
                     Area = 1/2 ab sin C

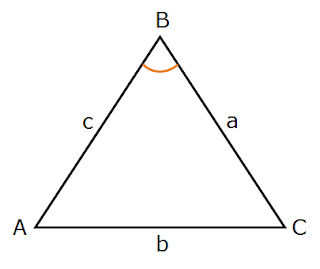
Area = 1/2 ac sin B

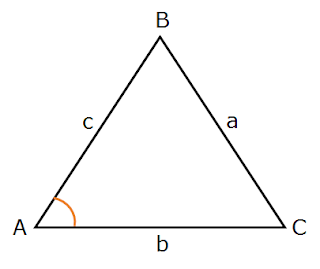
                        Area = 1/2 bc sin A

Related posts:

• Circumscribes and Inscribed Circles of Triangles
• Area of a Circle Formula and Problems with Solutions
• Congruence of Triangles – SSS, SAS, ASA, AAS and RHS
• Parallelograms on the same base and between the same parallels are equal in area
• Properties of a Rectangle – Geometry
• Triangle – Basics of Triangles – Definition and Properties
• What is a Rhombus Definition – Properties
• Elements of a Parallelogram
• Two triangles on the same base (or equal bases) and between the same parallels are equal in area
• Two triangles having the same base(or equal bases) and equal areas lie between the same parallels

Leave a Reply Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

AREA OF TRIANGLE WORD PROBLEMS

Problem 1 :

Each triangular  face of the Pyramid of Peace in  Kazakhstan is made up of 25 smaller equilateral  triangles. These triangles have measurements as  shown in the diagram. What is the area of one of the  smaller equilateral triangles ?

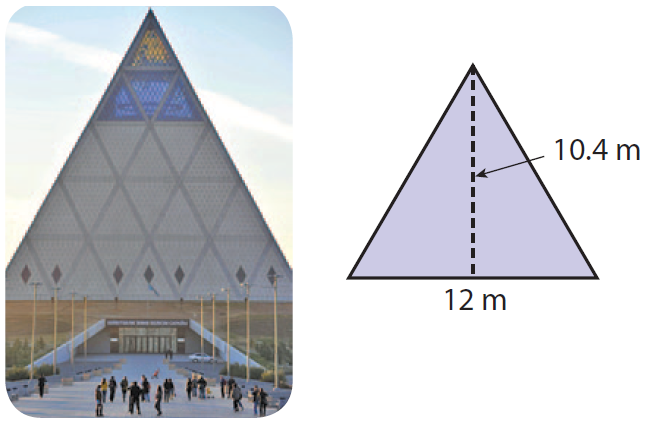
Area of  smaller equilateral  triangle is 

=  (1/2) x b x h

Substitute 2 for b and 10.4 for h. 

=  (1/2) x 12 x 10.4 

=  6 x 10.4

=  62.4 square meter

Problem 2 :

Amy needs to order a shade for a triangular-shaped window that has  a base of 6 feet and a height of 4 feet. What is the area of the shade ?

Since the shade is in the shape of triangle, we have to use the formula  for area of triangle to find the area of the shade.

Area of the shade is 

Substitute 6 for b and 4 for h. 

  =  (1/2) x 6 x 4

=  12 square feet

Example 3 :

Monica has a  triangular piece of fabric. The height of the  triangle is 15 inches and the triangle’s base  is 6 inches. Monica says that the area of  the fabric is 90 square inches . What error did Monica  make ? Explain your answer.

Area of the triangle is

Substitute 6 for b and 15 for h.

=  (1/2) x 6 x 15

=  15 x 3

=  45 square inches

Actual area of the triangular piece of fabric is 45 square inches. But Monica says that  area of  the fabric is 90 square inches. Which means, she forgot to multiply the product of base and height by 1/2. This is the error that she has made.  

Example 4 :

The sixth-grade art students are  making a mosaic using tiles in the shape  of right triangle. The two sides that meet to  form a right angle are 3 centimeters and 5 centimeters long. If there are 200 tiles in the  mosaic, what is the area of the mosaic ?

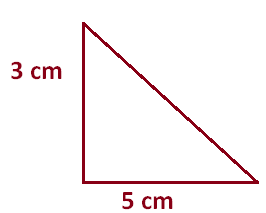
Area of each tile is 

Substitute 5 for b and 3 for h.

  =  (1/2) x 5 x 3

  =  7.5 cm ²

Area of 200 of  the  mosaic is

=  200 x 7.5

   =  1500  cm ²

Example 5 :

Wayne is going to paint the side of the house shown  in the diagram. What is the area that will be painted? Explain how you found your answer.

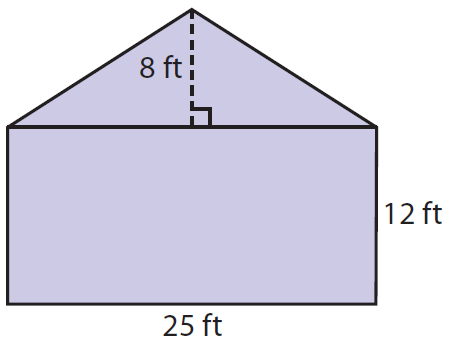
Wayne's house in the above picture is made up of using two shapes. One is triangle and and other one is rectangle. 

By finding the sum of areas of triangle and rectangle, we can get the required area that will be painted. 

Required area is

=  Area of triangle + Area of rectangle

  =  [(1/2 ) x b x h]  +  [l x w]

  =  [(1/2) x 25 x 8]  +  (25 x 12)

=  100 + 300

=  400 square ft

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Trigonometry Cofunction Identities

Apr 30, 24 09:01 PM

Worksheet on Unit Rates

Apr 30, 24 08:50 PM

Ratio Worksheet

Apr 29, 24 07:59 PM

Trending Post : Teaching Fractions with Food

50+ Free Area of Triangles Practice Problems | Fun Activities

This area of triangles practice worksheets contain 50+ area-related problems of a triangle. You can also conduct some triangle activities to teach this lesson through fun. These fun activities will help to understand the area of triangles practice and help students master this geometry skill.

Area of Triangles Practice with 4 Fun Games

We have generated 4 fun games for the area of triangles practice. There are 50+ free practice problems for your little ones to solve.

Scavenger Hunt

Puzzle Game

Bird House Game

Measurement Game

Unit Conversion

Area of Triangles: Definition with Examples

The area of a triangle refers to the space enclosed within its three sides.

To calculate the area of a triangle, we use a simple formula: Area = ½ x base x height . The “ base ” is the length of one side of the triangle, and the “ height ” is the perpendicular distance from that base to the opposite vertex.

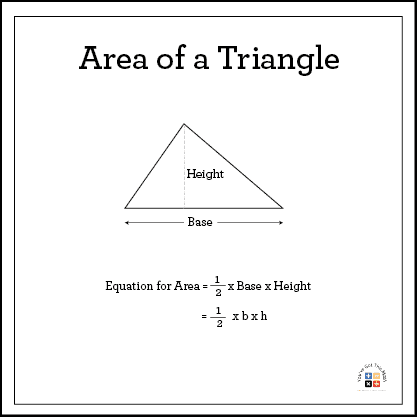
Let’s imagine a triangle with a base measuring 6 units and a height of 4 units. To find its area, we plug these values into the formula: Area = (6 × 4) ÷ 2 . Simplifying the equation, we get Area = 12 square units. So, the area of our triangle is 12 square units.

Area of Right Angle Triangles Practice with Scavenger Hunt

When there is an angle of 90° in a triangle it is called the right angle triangle. There is a base and a perpendicular side in the triangle. So, the area will be, Area = ½ x b x h The teachers can give the students a scavenger hunt game where the students will have to find the area of triangles practice. Follow the below steps to conduct this game.

• Firstly, gather all the students and make them a group.
• Provide them with some cards for the scavenger hunt. In this card, they will find some right-angle triangles. The base and the height will be given.
• The students will be asked to find the area.
• The answers will be distributed on the school premises. They should look for that.
• Finally, complete the task to finish the game.

Now, it’s time to practice the area of triangles. These PDF worksheets contain some problems in the area of triangles practice.

Puzzle Game for Area of Equilateral Triangles Practice

The equilateral triangle means where the three sides are equal and the angles are also equal. The area of the equilateral triangle is, Area = √3/4 a²

Here, “a” is the common side of the triangle.

The students need to acquire this Knowledge through fun. For this reason, we created a puzzle game to estimate the area of an equilateral triangle. Teachers can create puzzle cards like ours. The steps are stated below.

• Firstly, gather all the students and sit them down.
• Then, give them the puzzle cards where different kinds of equilateral triangles are situated having different colors.
• Students need to solve the puzzle by calculating the area through an equation.
• Lastly, finish the game by answering the area of triangles practice.

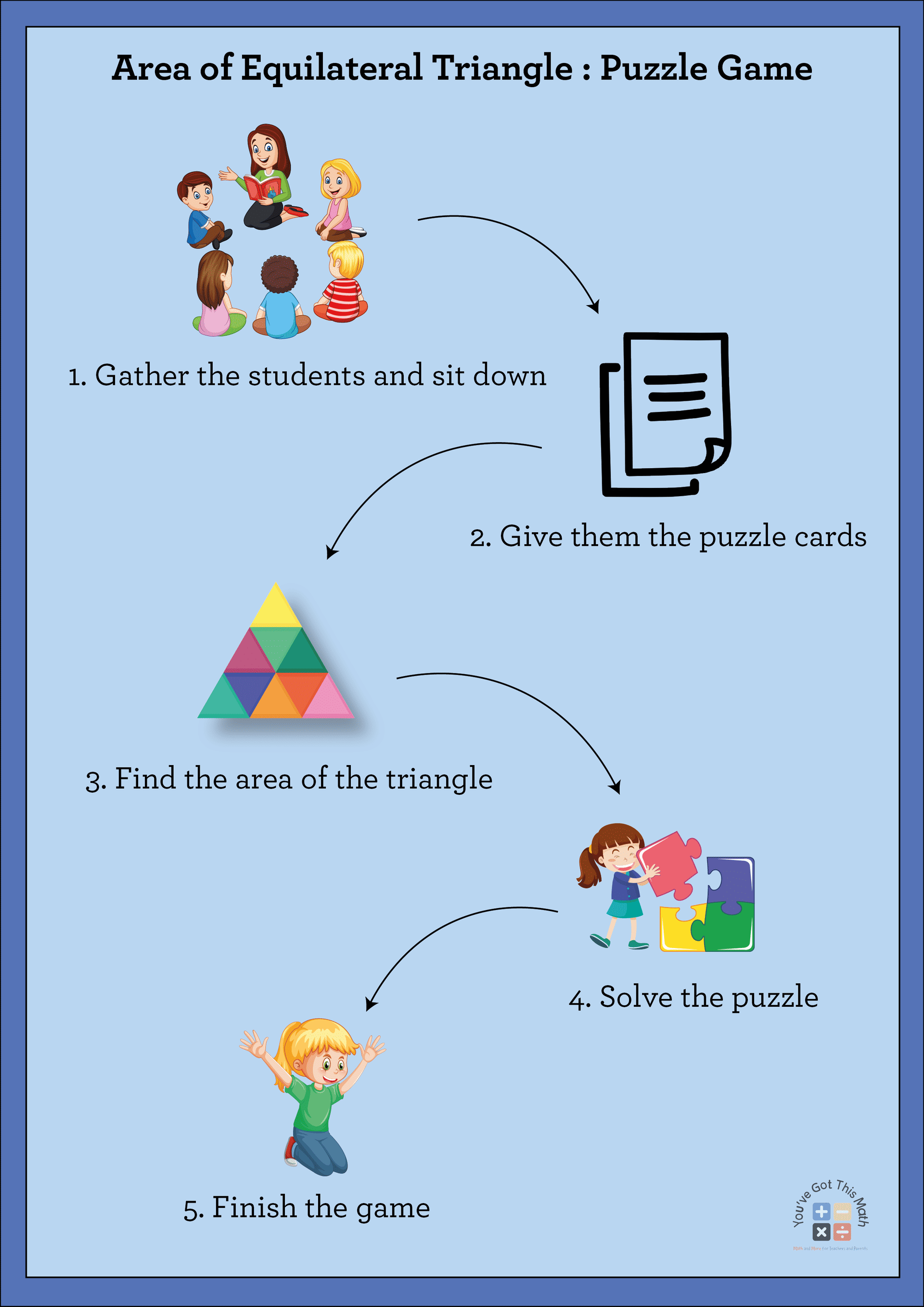
This is the PDF worksheet for the area of triangles practice. Solve the figures to find the area.

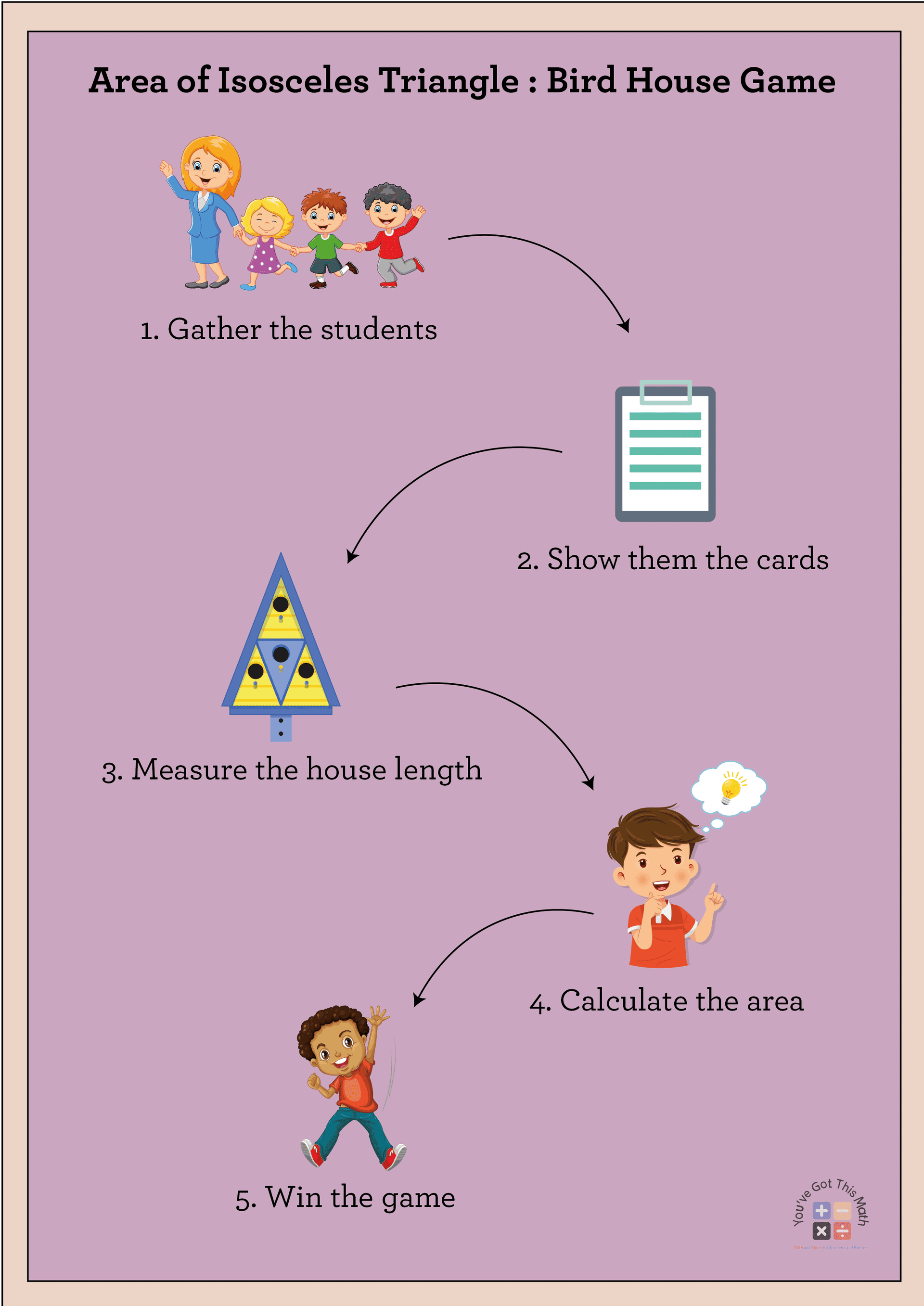
Area of Isosceles Triangles Practice with Bird House Game

The isosceles triangle is where the two arms are equal and the other is not. The area of an isosceles triangle is

Area = b/4 √(4a²-b²)

Where “a” is the equal side and “b” is the other side. You can introduce the students to isosceles triangle area practice through a birdhouse game.

• At the very beginning, gather all the students.
• Give them the card where they will write the answer.
• Give them a birdhouse whose shape is like an isosceles triangle.
• Students will measure the length and calculate the area through an equation.
• Win the game and have fun.😊

Provide this PDF worksheet to the students to solve the area of triangles practice.

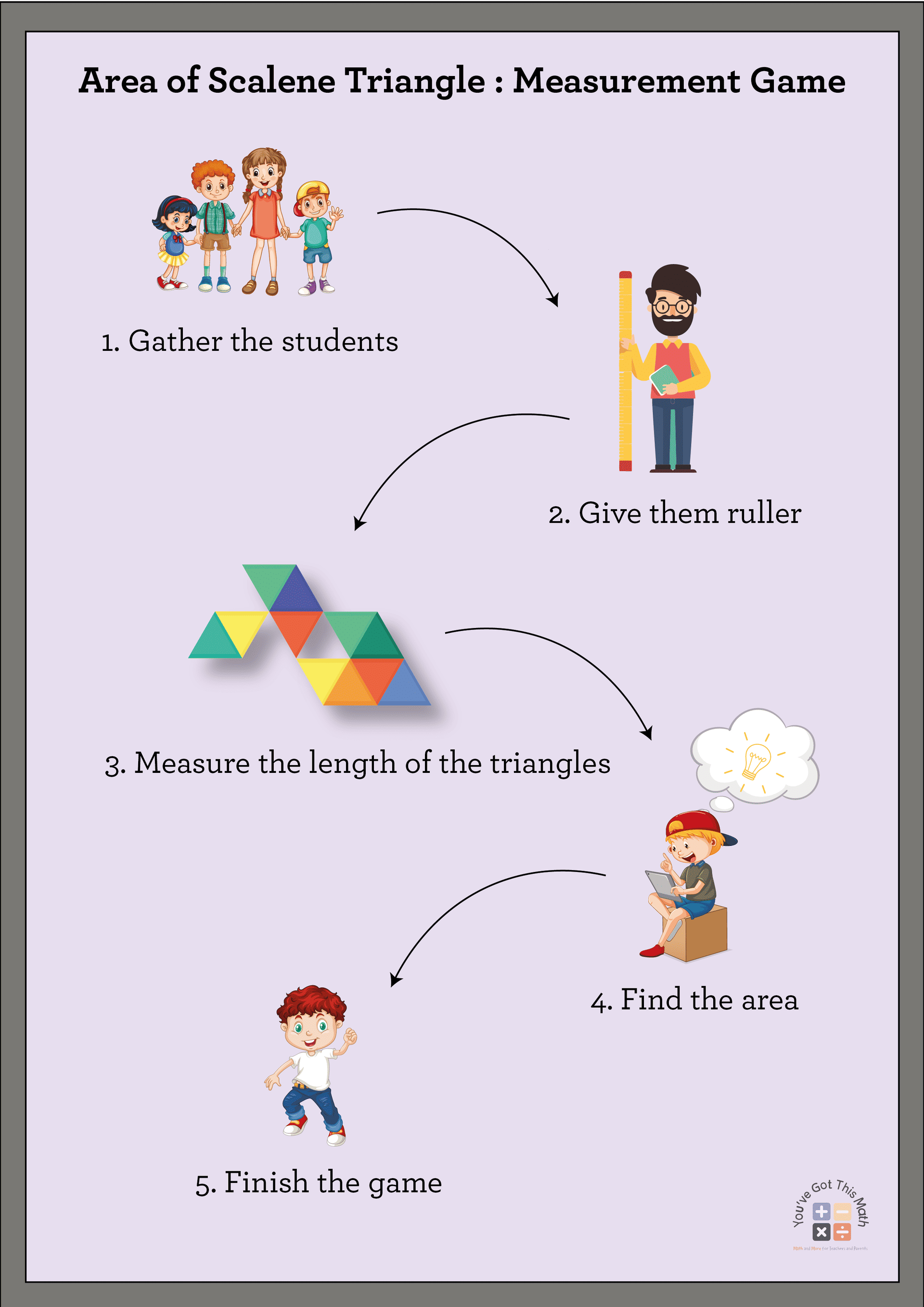
Measurement Game for Area of Scalene Triangles Practice

The scalene triangle is a triangle where all the sides are unequal. For this type of triangle, you need to find half of the perimeter first. Semi-perimeter, s = (a + b + c)/2 Then the area will be,

Area =  √{s x (s-a) x (s-b) x (s-c)

Where, a,b, and c are the three sides of the triangle and “s” is the semi-perimeter. This measurement skill will help the students to know more about the area of triangles practice.

• Gather them and give them a ruler. This will help them to measure the length of the triangles
• A card will contain different scalene triangles and the students will have to measure the length.
• From the length, the students need to estimate the area of triangles practice.
• Finish the game and win it.

Here is the PDF worksheet to calculate the area of triangles practice. Follow the triangles and practice them.

Unit Conversion for Area of Triangles Practice

This is so simple. You need to convert the units in the given format. Suppose you have a triangle whose base is 5 m and the height is 400 cm. What will be the area of this triangle in cm²?

Solution: Base = 5 m = 500 cm

              Height = 400 cm

             Area = ½ x 500 x 400

                      = 100000 cm²

Here is the PDF worksheet for the area of triangles practice. Practice them carefully to gain proper knowledge in the realm of the area of triangles practice.

Download Practice Worksheet PDF

This is the combination of all the worksheets together.

So these are the area of the triangle practice worksheet. These interactive worksheets will help the students to practice the area-related problems of a triangle. These games are also very interactive. Please, download the free printable practice sheet and give it to the students of 4th to 7th grade students.

Similar Posts

10 Free Witch 🧹 and Witch Hat Coloring Pages 🧹 PDF Printable

6 Free Fraction of a Set Word Problems Worksheet

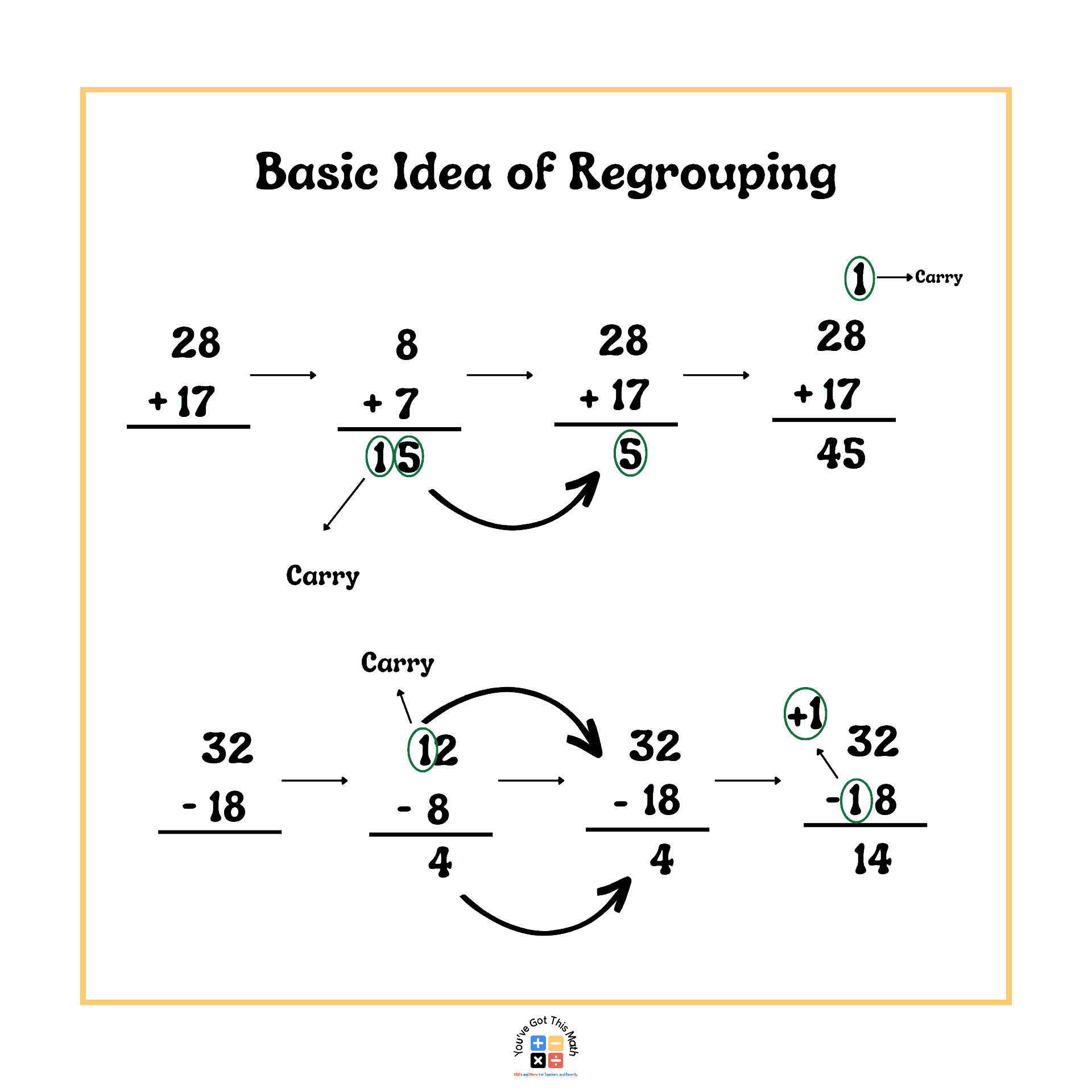
Regrouping in Math Examples | 80+ Problems | Free Printable

6 Free Adding and Subtracting Fractions with Regrouping Worksheet

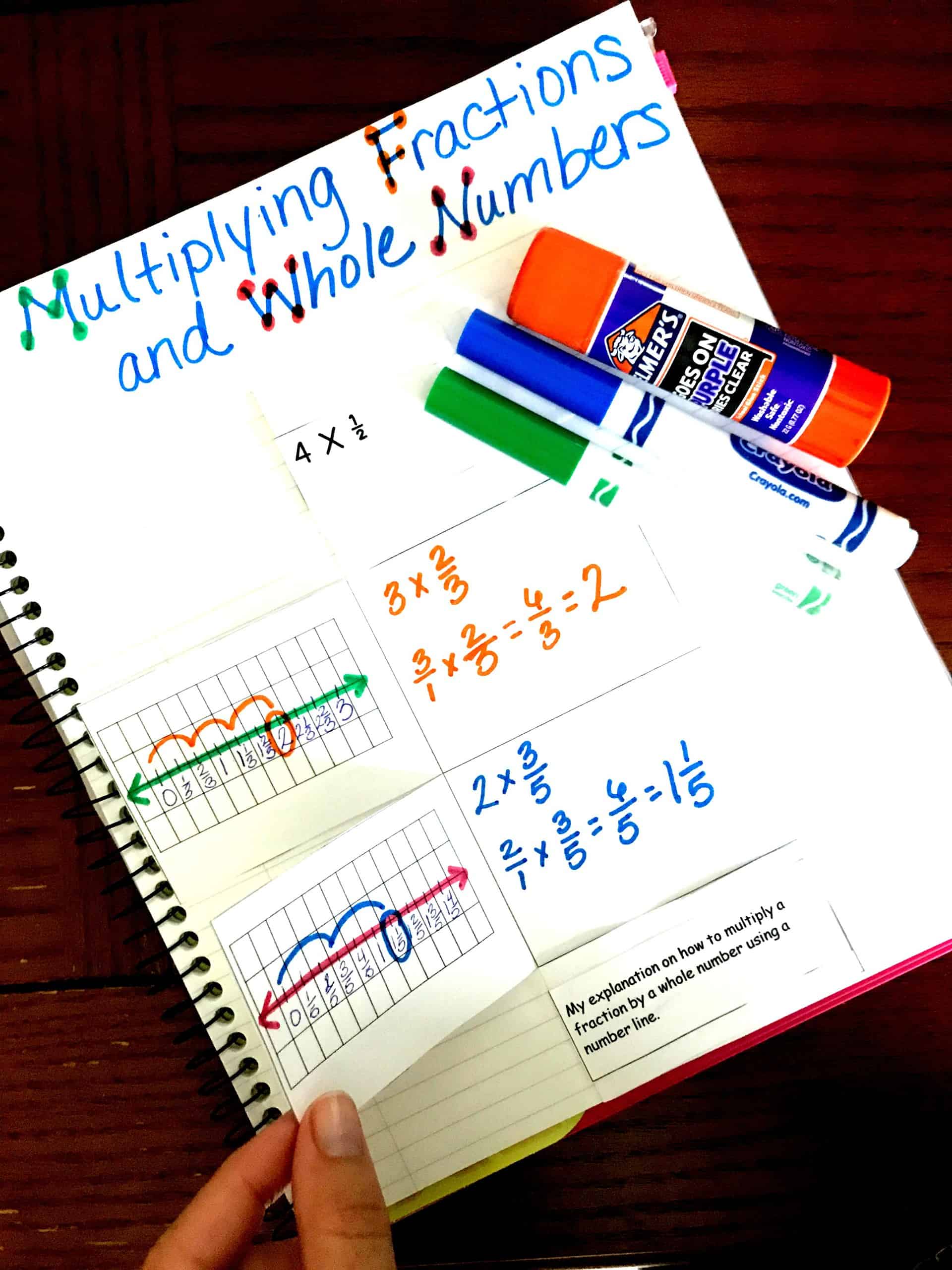
How to Multiply Fractions with Whole Numbers | Free Printable

Multi Digit Multiplication Word Problems | Free Worksheet

Triangle Area Calculator

Table of contents

This triangle area calculator can help in determining the triangle area. The basic triangle area formula needs to have a base and height given, but what if we don't have it? How can we calculate the area of a triangle with 3 sides only? The triangle area calculator is here for you. Give it a go! If you are still unsure how to find the area of a triangle, check the description below.

Triangle area formula

A triangle is one of the most basic shapes in geometry. The best known and the most straightforward formula, which almost everybody remembers from school, is:

• area = 0.5 × b × h , where b is the length of the base of the triangle, and h is the height/altitude of the triangle.

However, sometimes it's hard to find the height of the triangle. In that cases, many other equations may be used, depending on what you know about the triangle:

Three sides (SSS)

If you know the lengths of all sides, use the Heron's formula :

area = 0.25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c) )

Two sides and the angle between them (SAS)

You can calculate the area of a triangle easily from trigonometry:

area = 0.5 × a × b × sin(γ)

Two angles and a side between them (ASA)

There are different triangle area formulas versions - you can use, for example, trigonometry or law of sines to derive it:

area = a² × sin(β) × sin(γ) / (2 × sin(β + γ))

If you are looking for other formulas or calculators connected with triangles, check out this right triangle calculator , pythagorean theorem calculator , and law of cosines calculator .

How to use this triangle area calculator?

Assume that we know two sides and the angle between them:

• Type the first side length . It can be equal to 9 inches in our example.
• Determine the angle between two known sides . For example, 30 degrees.
• Enter the second triangle side . Let's choose 5 in.
• Watch our triangle area calculator performing all calculations for you! The area for our case is equal to 11.25 in².

How do I calculate the area of an equilateral triangle?

To calculate the area of an equilateral triangle, you only need to know the side:

area = a² × √3 / 4

Since √3 / 4 is approximately 0.433 , we can formulate a quick recipe: to approximate the area of an equilateral triangle, square the side's length and then multiply by 0.433 .

Although we prepared a separate calculator for the equilateral triangle area , you can quickly calculate it in this triangle area calculator. Simply use the subpart for the area of a triangle with 3 sides - as you know, every side has the same length in an equilateral triangle. It's possible to calculate that area also in the angle-side-angle or side-angle-side version - you probably remember that every angle in the equilateral triangle is equal to 60 degrees (π/3 rad).

How do I find the area of a triangle given sides?

If you know the lengths of all sides ( a , b , and c ) of a triangle, you can compute its area:

• Calculate half of the perimeter ½(a + b + c) . Denote this value by s .
• Compute s - a , s - b , and s - c .
• Multiply the three numbers from Step 2.
• Multiply the result by s .
• Take the square root of the result .
• This is the area of your triangle - well done! The method we've used is called Heron's formula .

How do I find the area of a triangle given angles?

You can't determine the area of a triangle if you know only the angles. This is because there are infinitely many triangles with the same angles . You must know at least one side (or height) of your triangle to determine its area.

How do I calculate the area of a right triangle?

To compute the area of a right triangle, you only need to multiply the lengths of the legs of your triangle and then divide the result by 2. For instance, if the legs are 3 in and 4 in, then the area is 3 × 4 /2 = 12 / 2 = 6 in sq.

What is the area of an equilateral triangle of side 10?

The area is approximately 43.3 . The precise answer is 25 × √3 . To get this answer, recall the formula for the area of an equilateral triangle of side a reads area = a 2 × √3 / 4 . For the triangle with side 10 we obtain area = 10 2 × √3 / 4 = 100 × √3 / 4 = 25 × √3 , which is approximately equal to 43.3 .

© Omni Calculator