mean hypothesis test calculator

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

t-test Calculator

When to use a t-test, which t-test, how to do a t-test, p-value from t-test, t-test critical values, how to use our t-test calculator, one-sample t-test, two-sample t-test, paired t-test, t-test vs z-test.

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

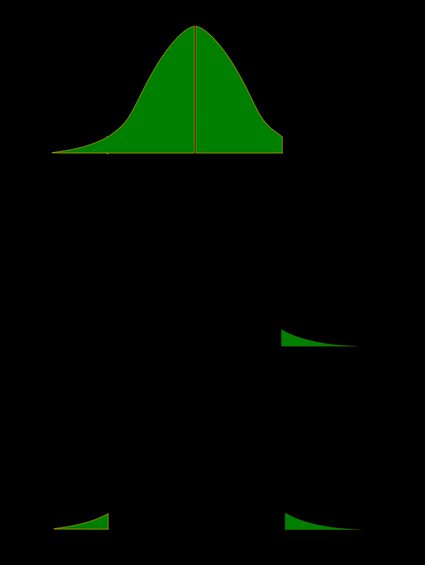
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

Books vs e-books

Error propagation, significant figures, venn diagram.

• Biology (100)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (509)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

28: Hypothesis Test for a Population Mean With Data Calculator

• Last updated
• Save as PDF
• Page ID 8350

• Larry Green
• Lake Tahoe Community College

Hypothesis Test for a Population Mean With Data Calculator

Type in the values from the data set separated by commas, for example, 2,4,5,8,11,2.  Then type in the population standard deviation \(\sigma\) if it is known or leave it blank if it is not known.  Then choose a left, right or two tailed test, and  the hypothesized mean.  Finally hit Calculate and the sample mean, the test statistic and the p-value will be shown.

Hypothesis Testing Calculator for Population Mean English Español

A free online hypothesis testing calculator for population mean to find the Hypothesis for the given population mean. Enter the sample mean, population mean, sample standard deviation, population size and the significance level to know the T score test value, P value and result of hypothesis.

Hypothesis Testing: Hypothesis Test, also known as Statistical Hypothesis Test is a method of statistical inference. Since it is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables, it is also referred to as confirmatory data analysis. The hypothesis testing for population mean analyses the results of the null hypothesis and the alternative hypothesis of a population. Hypothesis testing is one of the final analysis of statistical data. Use this free sample and population statistics calculator to perform a statistical hypothesis test for the given population mean. This online hypothesis testing calculator for population mean helps you to perform the two-tailed and one-tailed statistical hypothesis testing.

If you are performing one-tailed test for the sample mean of 20, population mean of 15, the size of the population of 5, SD of 25 and the significance level of -10, then you will get the below values as result.

Solution 1 :

T-score is 0.44721

Solution 2 :

P-value is 0.6726

P-value > -10 ( Significance level). Hence, H0 is not rejected. H0 is Null Hypothesis.

Related Calculators:

• Standard Deviation Calculator
• Population Confidence Interval
• Sample Size Calculator
• Mean Squared Error, Sum Of Squared Error Calculator
• Hypothesis Test For Population Variance
• Probability (P) Value T Test Calculator
• Cumulative Sum Calculator

Calculators and Converters

• Calculators
• Sample And Population Statistics

Top Calculators

Popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

T -Test Calculator for 2 Independent Means

Enter the values for your two treatment conditions into the text boxes below, either one score per line or as a comma delimited list. Select your significance level and whether your hypothesis is one or two-tailed. Then give your data a final check, and press the "Calculate T and P Values" button.

No calculation has yet been performed.

Other calculators ...

Free statistical calculators, test for one mean calculator, description, required input, computational notes.

This procedure calculates the difference of an observed mean with a hypothesized value. A significance value (P-value) and 95% Confidence Interval (CI) of the observed mean is reported. The P-value is the probability of obtaining the observed mean in the sample if the null hypothesis value were the true value.

The P-value is the area of the t distribution with n −1 degrees of freedom, that falls outside ± t (see Values of the t distribution table).

How to cite this page

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

• One sample t test

A one sample t test compares the mean with a hypothetical value. In most cases, the hypothetical value comes from theory. For example, if you express your data as 'percent of control', you can test whether the average differs significantly from 100. The hypothetical value can also come from previous data. For example, compare whether the mean systolic blood pressure differs from 135, a value determined in a previous study.

1. Choose data entry format

Caution: Changing format will erase your data.

2. Specify the hypothetical mean value

3. enter data, 4. view the results, learn more about the one sample t test.

In this article you will learn the requirements and assumptions of a one sample t test, how to format and interpret the results of a one sample t test, and when to use different types of t tests.

One sample t test: Overview

The one sample t test, also referred to as a single sample t test, is a statistical hypothesis test used to determine whether the mean calculated from sample data collected from a single group is different from a designated value specified by the researcher. This designated value does not come from the data itself, but is an external value chosen for scientific reasons. Often, this designated value is a mean previously established in a population, a standard value of interest, or a mean concluded from other studies. Like all hypothesis testing, the one sample t test determines if there is enough evidence reject the null hypothesis (H0) in favor of an alternative hypothesis (H1). The null hypothesis for a one sample t test can be stated as: "The population mean equals the specified mean value." The alternative hypothesis for a one sample t test can be stated as: "The population mean is different from the specified mean value."

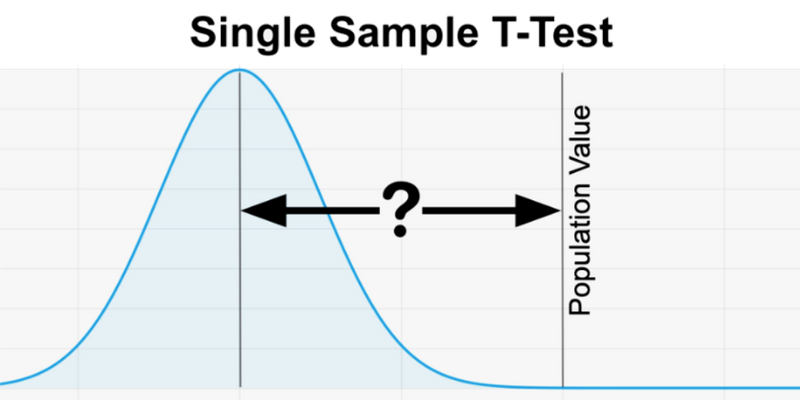
The one sample t test differs from most statistical hypothesis tests because it does not compare two separate groups or look at a relationship between two variables. It is a straightforward comparison between data gathered on a single variable from one population and a specified value defined by the researcher. The one sample t test can be used to look for a difference in only one direction from the standard value (a one-tailed t test ) or can be used to look for a difference in either direction from the standard value (a two-tailed t test ).

Requirements and Assumptions for a one sample t test

A one sample t test should be used only when data has been collected on one variable for a single population and there is no comparison being made between groups. For a valid one sample t test analysis, data values must be all of the following:

The one sample t test assumes that all "errors" in the data are independent. The term "error" refers to the difference between each value and the group mean. The results of a t test only make sense when the scatter is random - that whatever factor caused a value to be too high or too low affects only that one value. Prism cannot test this assumption, but there are graphical ways to explore data to verify this assumption is met.

A t test is only appropriate to apply in situations where data represent variables that are continuous measurements. As they rely on the calculation of a mean value, variables that are categorical should not be analyzed using a t test.

The results of a t test should be based on a random sample and only be generalized to the larger population from which samples were drawn.

As with all parametric hypothesis testing, the one sample t test assumes that you have sampled your data from a population that follows a normal (or Gaussian) distribution. While this assumption is not as important with large samples, it is important with small sample sizes, especially less than 10. If your data do not come from a Gaussian distribution , there are three options to accommodate this. One option is to transform the values to make the distribution more Gaussian, perhaps by transforming all values to their reciprocals or logarithms. Another choice is to use the Wilcoxon signed rank nonparametric test instead of the t test. A final option is to use the t test anyway, knowing that the t test is fairly robust to departures from a Gaussian distribution with large samples.

How to format a one sample t test

Ideally, data for a one sample t test should be collected and entered as a single column from which a mean value can be easily calculated. If data is entered on a table with multiple subcolumns, Prism requires one of the following choices to be selected to perform the analysis:

• Each subcolumn of data can be analyzed separately
• An average of the values in the columns across each row can be calculated, and the analysis conducted on this new stack of means, or
• All values in all columns can be treated as one sample of data (paying no attention to which row or column any values are in).

How the one sample t test calculator works

Prism calculates the t ratio by dividing the difference between the actual and hypothetical means by the standard error of the actual mean. The equation is written as follows, where x is the calculated mean, μ is the hypothetical mean (specified value), S is the standard deviation of the sample, and n is the sample size:

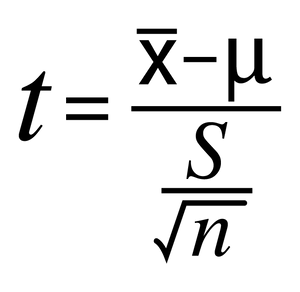
A p value is computed based on the calculated t ratio and the numbers of degrees of freedom present (which equals sample size minus 1). The one sample t test calculator assumes it is a two-tailed one sample t test, meaning you are testing for a difference in either direction from the specified value.

How to interpret results of a one sample t test

As discussed, a one sample t test compares the mean of a single column of numbers against a hypothetical mean. This hypothetical mean can be based upon a specific standard or other external prediction. The test produces a P value which requires careful interpretation.

The p value answers this question: If the data were sampled from a Gaussian population with a mean equal to the hypothetical value you entered, what is the chance of randomly selecting N data points and finding a mean as far (or further) from the hypothetical value as observed here?

If the p value is large (usually defined to mean greater than 0.05), the data do not give you any reason to conclude that the population mean differs from the designated value to which it has been compared. This is not the same as saying that the true mean equals the hypothetical value, but rather states that there is no evidence of a difference. Thus, we cannot reject the null hypothesis (H0).

If the p value is small (usually defined to mean less than or equal to 0.05), then it is unlikely that the discrepancy observed between the sample mean and hypothetical mean is due to a coincidence arising from random sampling. There is evidence to reject the idea that the difference is coincidental and conclude instead that the population has a mean that is different from the hypothetical value to which it has been compared. The difference is statistically significant, and the null hypothesis is therefore rejected.

If the null hypothesis is rejected, the question of whether the difference is scientifically important still remains. The confidence interval can be a useful tool in answering this question. Prism reports the 95% confidence interval for the difference between the actual and hypothetical mean. In interpreting these results, one can be 95% sure that this range includes the true difference. It requires scientific judgment to determine if this difference is truly meaningful.

Performing t tests? We can help.

Sign up for more information on how to perform t tests and other common statistical analyses.

When to use different types of t tests

There are three types of t tests which can be used for hypothesis testing:

• Independent two-sample (or unpaired) t test
• Paired sample t test

As described, a one sample t test should be used only when data has been collected on one variable for a single population and there is no comparison being made between groups. It only applies when the mean value for data is intended to be compared to a fixed and defined number.

In most cases involving data analysis, however, there are multiple groups of data either representing different populations being compared, or the same population being compared at different times or conditions. For these situations, it is not appropriate to use a one sample t test. Other types of t tests are appropriate for these specific circumstances:

Independent Two-Sample t test (Unpaired t test)

The independent sample t test, also referred to as the unpaired t test, is used to compare the means of two different samples. The independent two-sample t test comes in two different forms:

• the standard Student's t test, which assumes that the variance of the two groups are equal.
• the Welch's t test , which is less restrictive compared to the original Student's test. This is the test where you do not assume that the variance is the same in the two groups, which results in fractional degrees of freedom.

The two methods give very similar results when the sample sizes are equal and the variances are similar.

Paired Sample t test

The paired sample t test is used to compare the means of two related groups of samples. Put into other words, it is used in a situation where you have two values (i.e., a pair of values) for the same group of samples. Often these two values are measured from the same samples either at two different times, under two different conditions, or after a specific intervention.

You can perform multiple independent two-sample comparison tests simultaneously in Prism. Select from parametric and nonparametric tests and specify if the data are unpaired or paired. Try performing a t test with a 30-day free trial of Prism .

Watch this video to learn how to choose between a paired and unpaired t test.

Example of how to apply the appropriate t test

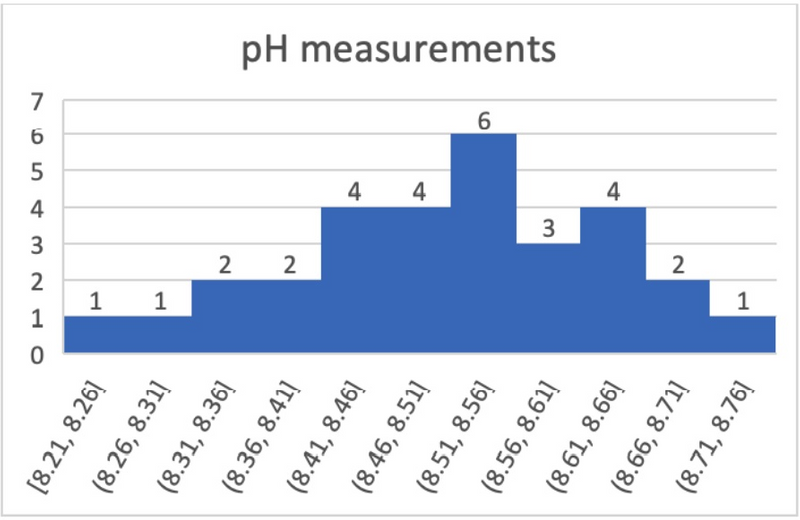
"Alkaline" labeled bottled drinking water has become fashionable over the past several years. Imagine we have collected a random sample of 30 bottles of "alkaline" drinking water from a number of different stores to represent the population of "alkaline" bottled water for a particular brand available to the general consumer. The labels on each of the bottles claim that the pH of the "alkaline" water is 8.5. A laboratory then proceeds to measure the exact pH of the water in each bottle.

Table 1: pH of water in random sample of "alkaline bottled water"

If you look at the table above, you see that some bottles have a pH measured to be lower than 8.5, while other bottles have a pH measured to be higher. What can the data tell us about the actual pH levels found in this brand of "alkaline" water bottles marketed to the public as having a pH of 8.5? Statistical hypothesis testing provides a sound method to evaluate this question. Which specific test to use, however, depends on the specific question being asked.

Is a t test appropriate to apply to this data?

Let's start by asking: Is a t test an appropriate method to analyze this set of pH data? The following list reviews the requirements and assumptions for using a t test:

• Independent sampling : In an independent sample t test, the data values are independent. The pH of one bottle of water does not depend on the pH of any other water bottle. (An example of dependent values would be if you collected water bottles from a single production lot. A sample from a single lot is representative only of that lot, not of alkaline bottled water in general).
• Continuous variable : The data values are pH levels, which are numerical measurements that are continuous.
• Random sample : We assume the water bottles are a simple random sample from the population of "alkaline" water bottles produced by this brand as they are a mix of many production lots.
• Normal distribution : We assume the population from which we collected our samples has pH levels that are normally distributed. To verify this, we should visualize the data graphically. The figure below shows a histogram for the pH measurements of the water bottles. From a quick look at the histogram, we see that there are no unusual points, or outliers. The data look roughly bell-shaped, so our assumption of a normal distribution seems reasonable. The QQ plot can also be used to graphically assess normality and is the preferred choice when the sample size is small.

Based upon these features and assumptions being met, we can conclude that a t test is an appropriate method to be applied to this set of data.

Which t test is appropriate to use?

The next decision is which t test to apply, and this depends on the exact question we would like our analysis to answer. This example illustrates how each type of t test could be chosen for a specific analysis, and why the one sample t test is the correct choice to determine if the measured pH of the bottled water samples match the advertised pH of 8.5.

We could be interested in determining whether a certain characteristic of a water bottle is associated with having a higher or lower pH, such as whether bottles are glass or plastic. For this questions, we would effectively be dividing the bottles into 2 separate groups and comparing the means of the pH between the 2 groups. For this analysis, we would elect to use a two sample t test because we are comparing the means of two independent groups.

We could also be interested in learning if pH is affected by a water bottle being opened and exposed to the air for a week. In this case, each original sample would be tested for pH level after a week had elapsed and the water had been exposed to the air, creating a second set of sample data. To evaluate whether this exposure affected pH, we would again be comparing two different groups of data, but this time the data are in paired samples each having an original pH measurement and a second measurement from after the week of exposure to the open air. For this analysis, it is appropriate to use a paired t test so that data for each bottle is assembled in rows, and the change in pH is considered bottle by bottle.

Returning to the original question we set out to answer-whether bottled water that is advertised to have a pH of 8.5 actually meets this claim-it is now clear that neither an independent two sample t test or a paired t test would be appropriate. In this case, all 30 pH measurements are sampled from one group representing bottled drinking water labeled "alkaline" available to the general consumer. We wish to compare this measured mean with an expected advertised value of 8.5. This is the exact situation for which one should employ a one sample t test!

From a quick look at the descriptive statistics, we see that the mean of the sample measurements is 8.513, slightly above 8.5. Does this average from our sample of 30 bottles validate the advertised claim of pH 8.5? By applying Prism's one sample t test analysis to this data set, we will get results by which we can evaluate whether the null hypothesis (that there is no difference between the mean pH level in the water bottles and the pH level advertised on the bottles) should be accepted or rejected.

How to Perform a One Sample T Test in Prism

In prior versions of Prism, the one sample t test and the Wilcoxon rank sum tests were computed as part of Prism's Column Statistics analysis. Now, starting with Prism 8, performing one sample t tests is even easier with a separate analysis in Prism.

Steps to perform a one sample t test in Prism

• Create a Column data table.
• Enter each data set in a single Y column so all values from each group are stacked into a column. Prism will perform a one sample t test (or Wilcoxon rank sum test) on each column you enter.
• Click Analyze, look in the list of Column analyses, and choose one sample t test and Wilcoxon test.

It's that simple! Prism streamlines your t test analysis so you can make more accurate and more informed data interpretations. Start your 30-day free trial of Prism and try performing your first one sample t test in Prism.

Watch this video for a step-by-step tutorial on how to perform a t test in Prism.

We Recommend:

Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required.

Hypothesis Test for a Mean

Use the calculator below to analyze the results of a hypothesis test for a mean. Enter your null hypothesis's mean, sample mean, sample standard deviation, sample size, test type, and significance level to find your results.

You will find a description of how to conduct a hypothesis test of a mean below the calculator.

Define the t-test

Sample mean under the null distribution, conducting single mean hypothesis tests.

A hypothesis test of a sample mean can help you make inferences about the population from which you drew it. It is a tool to determine what is probably true about an event or phenomena.

Testing a Mean

For the results of a hypothesis test of a mean to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Simple Random Sampling - You should collect your sample with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normal Sampling Distribution -The sampling distribution should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test for a mean.

The null hypothesis, is a skeptical claim that you would like to test. It is defined by the null hypothesis's mean, which is often labeled μ 0 .

The alternative hypothesis represents an alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ ≠ μ 0 requires a two-tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null sampling distribution. For example, in a one-tail test evaluating if the sampling distribution is above the null sampling distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ > μ 0 and μ 0 alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal Distribution with the following parameters:

• The Population Mean, μ - The population mean is assumed to be the null hypothesis's mean in a single mean hypothesis test.
• The Standard Error, SE - For samples that are much smaller than the population, the standard error can be computed as follows: SE = s / sqrt(n), with s being the sample standard deviation and n being the sample size. It defines how sample means are expected to vary around the null hypothesis's mean given the sample size and under the assumption that the null hypothesis is true.
• Degrees of Freedom, DF - For hypothesis tests for a single mean, the degrees of freedom equals n – 1, with n being the sample size.

In a hypothesis test for a mean, we calculate the probability that we would observe the sample mean, x̄, assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ - μ 0 ) / SE

The t-score is a test statistic that tells us how far our observation is from the null hypothesis's mean under the null distribution. Using any t-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for a mean is sometimes known as a t-test because of the use of a t-score in analyzing results.

If you find the probability is below the significance level, we reject the null hypothesis.

The conclusion of a hypothesis test for a mean is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample mean is the true population mean. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.

A hypothesis test is simply a way to look at a sample and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for a Mean

Let’s say that you manage a clothing store with a historical average transaction amount of $53.24.

You believe the best way to improve your business is to increase your average sale amount. So, you have been working hard on training your sales staff on how sell more items to customers to increase sales.

To test if your sales training has increased your average sale amount, you decide to run a hypothesis test for a mean with a sample of 50 transactions to see if your average sale amount has increased.

• Check the conditions - You collect your sample using simple random sampling , and you know that historically your transactions are normally distributed about the average transaction. So, your conditions for running a hypothesis test for a mean are satisfied.
• State Your Hypothesis - Your null hypothesis is that your average transaction amount is the same or less than the historical average, formally stated μ ≤ $53.24. Your alternative hypothesis is that your average is greater than the historical average, formally stated μ > $53.24.
• Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is one-tail test, you will evaluate if your sample mean would occur at the upper 5% of the null distribution.
• Analyze Your Sample - After collecting your sample (which you do after steps 1-3), you find that the sample mean, x̄, transaction amount is $61.02 with a standard deviation of $39.12. Using the calculator above, you find that a sample mean of $61.02 would results in a t-score of 1.41 under the null distribution, which translates to a p-value of 8.30%.
• Interpret Your Results - Since your p-value of 8.30% is greater than the significance level of 5%, you do not have sufficient evidence to reject the null hypothesis.

In this example, you found that you cannot reject the claim that your current transaction amount is less than or equal to your historical transaction amount of $53.24. Your results do not guarantee that your transaction amount is $53.24 or below, but they do indicate that your sales training has likely not had the effect that you wanted on your store's average sale amount.

• 1-800-234-2933
• [email protected]

Hypothesis testing for the mean Calculator

How does the Hypothesis testing for the mean Calculator work?

What 1 formula is used for the hypothesis testing for the mean calculator, what 7 concepts are covered in the hypothesis testing for the mean calculator.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Courses
• Our Experts

Top Categories

• Development
• Photography
• Refer a Friend
• Festival Offer
• Limited Membership
• Scholarship

“extremely user friendly”

“truly amazing!”

“so easy to use!”

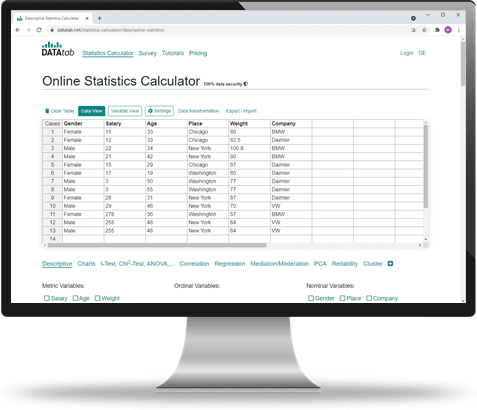
Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

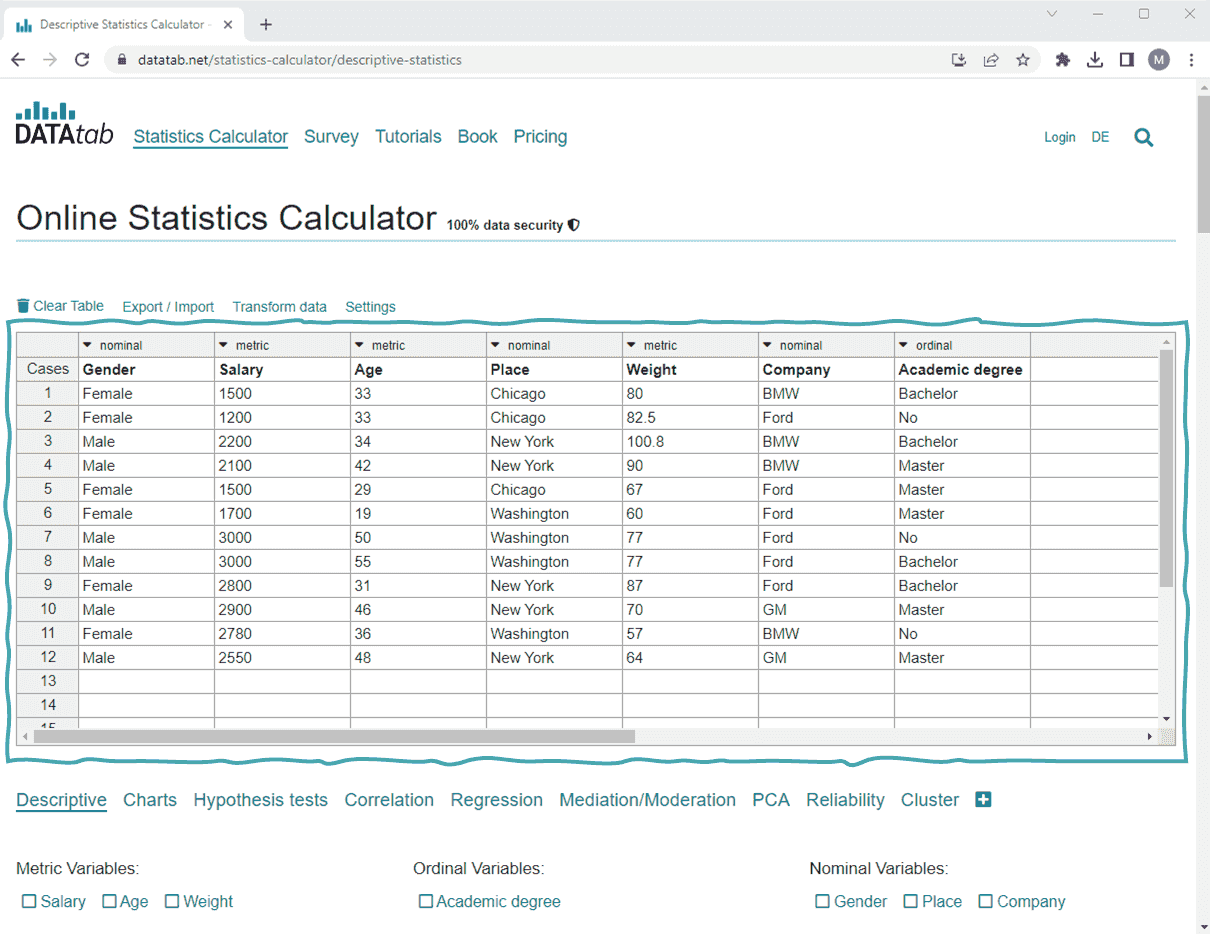
Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

Hypothesis Testing Calculator

Navigating hypothesis testing: unveiling the potential of the hypothesis testing calculator.

Embarking on the journey of statistical exploration, hypothesis testing stands out as an indispensable method for informed decision-making and drawing meaningful conclusions from data. Whether you find yourself in the academic realm, engaged in research endeavors, or navigating the professional landscape, having a trustworthy Hypothesis Testing Calculator in your statistical toolkit can prove to be a game-changer. Let’s delve into the intricacies of hypothesis testing and uncover how this calculator can be your ally in statistical analyses.

Demystifying Hypothesis Testing:

Null Hypothesis (H0): Positioned as the default assumption, the null hypothesis asserts the absence of any significant difference or effect and is commonly represented as H0.

Alternative Hypothesis (Ha): In direct contradiction to the null hypothesis, the alternative hypothesis posits the existence of a noteworthy difference or effect, denoted as Ha.

Significance Level (α): Acting as the predetermined threshold, typically set at 0.05 or 5%, the significance level plays a pivotal role in determining statistical significance. Should the calculated p-value fall below α, the null hypothesis is rejected.

p-value: Representing the likelihood of observing the results, or more extreme outcomes, under the assumption of the null hypothesis being true, a smaller p-value suggests the unlikelihood of the results occurring by chance.

Features that Define the Hypothesis Testing Calculator:

Input Parameters: The calculator demands input of sample data, selection of the test type (e.g., t-test, chi-square test), specification of null and alternative hypotheses, and determination of the significance level.

Calculations: Once armed with the requisite data and parameters, the calculator diligently executes statistical tests and computations. The output encompasses crucial details like the test statistic, degrees of freedom, and the all-important p-value.

Interpretation: Armed with the results, the calculator aids in the decision-making process, guiding whether to reject or accept the null hypothesis. An interpretation of the findings is provided, playing a pivotal role in drawing insightful conclusions.

Visual Representation: Some calculators go the extra mile by offering visual aids such as graphs or charts, facilitating a deeper understanding of data distribution and test outcomes.

Unveiling the Significance of the Hypothesis Testing Calculator:

In Scientific Research: Researchers spanning diverse fields leverage hypothesis testing to validate their hypotheses, thereby extracting meaningful insights from data.

In Quality Control: Industries rely on hypothesis testing as a quality assurance mechanism, ensuring the consistency and excellence of products and processes.

In Medical Studies: Within the realm of medical research, hypothesis testing serves as a critical tool for evaluating the effectiveness of treatments or interventions.

In Academics: Both students and educators find value in hypothesis testing as an educational tool, enabling the comprehension of statistical concepts and the conduct of experiments.

In Data-Driven Decision-Making: Businesses, keen on making decisions grounded in data, turn to hypothesis testing to navigate choices such as launching a new product based on comprehensive market research.

Concluding Insights:

The Hypothesis Testing Calculator emerges as a formidable ally, simplifying intricate statistical analyses and fostering data-driven decision-making. Whether you are in the midst of experimental undertakings, scrutinizing survey data, or overseeing quality control protocols, a solid understanding of hypothesis testing coupled with the use of this calculator empowers you to make well-informed choices. In doing so, you not only contribute to evidence-based research but also play a pivotal role in shaping decision-making processes across various domains.

• FOR INSTRUCTOR
• FOR INSTRUCTORS

8.4.3 Hypothesis Testing for the Mean

$\quad$ $H_0$: $\mu=\mu_0$, $\quad$ $H_1$: $\mu \neq \mu_0$.

$\quad$ $H_0$: $\mu \leq \mu_0$, $\quad$ $H_1$: $\mu > \mu_0$.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$.

Two-sided Tests for the Mean:

Therefore, we can suggest the following test. Choose a threshold, and call it $c$. If $|W| \leq c$, accept $H_0$, and if $|W|>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have

• As discussed above, we let \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} Note that, assuming $H_0$, $W \sim N(0,1)$. We will choose a threshold, $c$. If $|W| \leq c$, we accept $H_0$, and if $|W|>c$, accept $H_1$. To choose $c$, we let \begin{align} P(|W| > c \; | \; H_0) =\alpha. \end{align} Since the standard normal PDF is symmetric around $0$, we have \begin{align} P(|W| > c \; | \; H_0) = 2 P(W>c | \; H_0). \end{align} Thus, we conclude $P(W>c | \; H_0)=\frac{\alpha}{2}$. Therefore, \begin{align} c=z_{\frac{\alpha}{2}}. \end{align} Therefore, we accept $H_0$ if \begin{align} \left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \leq z_{\frac{\alpha}{2}}, \end{align} and reject it otherwise.
• We have \begin{align} \beta (\mu) &=P(\textrm{type II error}) = P(\textrm{accept }H_0 \; | \; \mu) \\ &= P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right). \end{align} If $X_i \sim N(\mu,\sigma^2)$, then $\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$. Thus, \begin{align} \beta (\mu)&=P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right)\\ &=P\left(\mu_0- z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \overline{X} \leq \mu_0+ z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\right)\\ &=\Phi\left(z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right)-\Phi\left(-z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right). \end{align}
• Let $S^2$ be the sample variance for this random sample. Then, the random variable $W$ defined as \begin{equation} W(X_1,X_2, \cdots, X_n)=\frac{\overline{X}-\mu_0}{S / \sqrt{n}} \end{equation} has a $t$-distribution with $n-1$ degrees of freedom, i.e., $W \sim T(n-1)$. Thus, we can repeat the analysis of Example 8.24 here. The only difference is that we need to replace $\sigma$ by $S$ and $z_{\frac{\alpha}{2}}$ by $t_{\frac{\alpha}{2},n-1}$. Therefore, we accept $H_0$ if \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}, \end{align} and reject it otherwise. Let us look at a numerical example of this case.

$\quad$ $H_0$: $\mu=170$, $\quad$ $H_1$: $\mu \neq 170$.

• Let's first compute the sample mean and the sample standard deviation. The sample mean is \begin{align}%\label{} \overline{X}&=\frac{X_1+X_2+X_3+X_4+X_5+X_6+X_7+X_8+X_9}{9}\\ &=165.8 \end{align} The sample variance is given by \begin{align}%\label{} {S}^2=\frac{1}{9-1} \sum_{k=1}^9 (X_k-\overline{X})^2&=68.01 \end{align} The sample standard deviation is given by \begin{align}%\label{} S&= \sqrt{S^2}=8.25 \end{align} The following MATLAB code can be used to obtain these values: x=[176.2,157.9,160.1,180.9,165.1,167.2,162.9,155.7,166.2]; m=mean(x); v=var(x); s=std(x); Now, our test statistic is \begin{align} W(X_1,X_2, \cdots, X_9)&=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}\\ &=\frac{165.8-170}{8.25 / 3}=-1.52 \end{align} Thus, $|W|=1.52$. Also, we have \begin{align} t_{\frac{\alpha}{2},n-1} = t_{0.025,8} \approx 2.31 \end{align} The above value can be obtained in MATLAB using the command $\mathtt{tinv(0.975,8)}$. Thus, we conclude \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}. \end{align} Therefore, we accept $H_0$. In other words, we do not have enough evidence to conclude that the average height in the city is different from the average height in the country.

Let us summarize what we have obtained for the two-sided test for the mean.

One-sided Tests for the Mean:

• As before, we define the test statistic as \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} If $H_0$ is true (i.e., $\mu \leq \mu_0$), we expect $\overline{X}$ (and thus $W$) to be relatively small, while if $H_1$ is true, we expect $\overline{X}$ (and thus $W$) to be larger. This suggests the following test: Choose a threshold, and call it $c$. If $W \leq c$, accept $H_0$, and if $W>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have \begin{align} P(\textrm{type I error}) &= P(\textrm{Reject }H_0 \; | \; H_0) \\ &= P(W > c \; | \; \mu \leq \mu_0) \leq \alpha. \end{align} Here, the probability of type I error depends on $\mu$. More specifically, for any $\mu \leq \mu_0$, we can write \begin{align} P(\textrm{type I error} \; | \; \mu) &= P(\textrm{Reject }H_0 \; | \; \mu) \\ &= P(W > c \; | \; \mu)\\ &=P \left(\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}+\frac{\mu-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c+\frac{\mu_0-\mu}{\sigma / \sqrt{n}} \; | \; \mu\right)\\ &\leq P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c \; | \; \mu\right) \quad (\textrm{ since }\mu \leq \mu_0)\\ &=1-\Phi(c) \quad \big(\textrm{ since given }\mu, \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1) \big). \end{align} Thus, we can choose $\alpha=1-\Phi(c)$, which results in \begin{align} c=z_{\alpha}. \end{align} Therefore, we accept $H_0$ if \begin{align} \frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \leq z_{\alpha}, \end{align} and reject it otherwise.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$,

P-value Calculator

Statistical significance calculator to easily calculate the p-value and determine whether the difference between two proportions or means (independent groups) is statistically significant. T-test calculator & z-test calculator to compute the Z-score or T-score for inference about absolute or relative difference (percentage change, percent effect). Suitable for analysis of simple A/B tests.

Related calculators

• Using the p-value calculator
• What is "p-value" and "significance level"
• P-value formula
• Why do we need a p-value?
• How to interpret a statistically significant result / low p-value
• P-value and significance for relative difference in means or proportions

    Using the p-value calculator

This statistical significance calculator allows you to perform a post-hoc statistical evaluation of a set of data when the outcome of interest is difference of two proportions (binomial data, e.g. conversion rate or event rate) or difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.). You can use a Z-test (recommended) or a T-test to find the observed significance level (p-value statistic). The Student's T-test is recommended mostly for very small sample sizes, e.g. n < 30. In order to avoid type I error inflation which might occur with unequal variances the calculator automatically applies the Welch's T-test instead of Student's T-test if the sample sizes differ significantly or if one of them is less than 30 and the sampling ratio is different than one.

If entering proportions data, you need to know the sample sizes of the two groups as well as the number or rate of events. These can be entered as proportions (e.g. 0.10), percentages (e.g. 10%) or just raw numbers of events (e.g. 50).

If entering means data, simply copy/paste or type in the raw data, each observation separated by comma, space, new line or tab. Copy-pasting from a Google or Excel spreadsheet works fine.

The p-value calculator will output : p-value, significance level, T-score or Z-score (depending on the choice of statistical hypothesis test), degrees of freedom, and the observed difference. For means data it will also output the sample sizes, means, and pooled standard error of the mean. The p-value is for a one-sided hypothesis (one-tailed test), allowing you to infer the direction of the effect (more on one vs. two-tailed tests ). However, the probability value for the two-sided hypothesis (two-tailed p-value) is also calculated and displayed, although it should see little to no practical applications.

Warning: You must have fixed the sample size / stopping time of your experiment in advance, otherwise you will be guilty of optional stopping (fishing for significance) which will inflate the type I error of the test rendering the statistical significance level unusable. Also, you should not use this significance calculator for comparisons of more than two means or proportions, or for comparisons of two groups based on more than one metric. If a test involves more than one treatment group or more than one outcome variable you need a more advanced tool which corrects for multiple comparisons and multiple testing. This statistical calculator might help.

    What is "p-value" and "significance level"

The p-value is a heavily used test statistic that quantifies the uncertainty of a given measurement, usually as a part of an experiment, medical trial, as well as in observational studies. By definition, it is inseparable from inference through a Null-Hypothesis Statistical Test (NHST) . In it we pose a null hypothesis reflecting the currently established theory or a model of the world we don't want to dismiss without solid evidence (the tested hypothesis), and an alternative hypothesis: an alternative model of the world. For example, the statistical null hypothesis could be that exposure to ultraviolet light for prolonged periods of time has positive or neutral effects regarding developing skin cancer, while the alternative hypothesis can be that it has a negative effect on development of skin cancer.

In this framework a p-value is defined as the probability of observing the result which was observed, or a more extreme one, assuming the null hypothesis is true . In notation this is expressed as:

p(x 0 ) = Pr(d(X) > d(x 0 ); H 0 )

where x 0 is the observed data (x 1 ,x 2 ...x n ), d is a special function (statistic, e.g. calculating a Z-score), X is a random sample (X 1 ,X 2 ...X n ) from the sampling distribution of the null hypothesis. This equation is used in this p-value calculator and can be visualized as such:

Therefore the p-value expresses the probability of committing a type I error : rejecting the null hypothesis if it is in fact true. See below for a full proper interpretation of the p-value statistic .

Another way to think of the p-value is as a more user-friendly expression of how many standard deviations away from the normal a given observation is. For example, in a one-tailed test of significance for a normally-distributed variable like the difference of two means, a result which is 1.6448 standard deviations away (1.6448σ) results in a p-value of 0.05.

The term "statistical significance" or "significance level" is often used in conjunction to the p-value, either to say that a result is "statistically significant", which has a specific meaning in statistical inference ( see interpretation below ), or to refer to the percentage representation the level of significance: (1 - p value), e.g. a p-value of 0.05 is equivalent to significance level of 95% (1 - 0.05 * 100). A significance level can also be expressed as a T-score or Z-score, e.g. a result would be considered significant only if the Z-score is in the critical region above 1.96 (equivalent to a p-value of 0.025).

    P-value formula

There are different ways to arrive at a p-value depending on the assumption about the underlying distribution. This tool supports two such distributions: the Student's T-distribution and the normal Z-distribution (Gaussian) resulting in a T test and a Z test, respectively.

In both cases, to find the p-value start by estimating the variance and standard deviation, then derive the standard error of the mean, after which a standard score is found using the formula [2] :

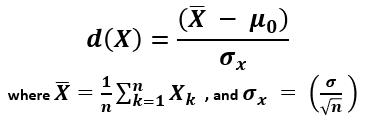
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).

When calculating a p-value using the Z-distribution the formula is Φ(Z) or Φ(-Z) for lower and upper-tailed tests, respectively. Φ is the standard normal cumulative distribution function and a Z-score is computed. In this mode the tool functions as a Z score calculator.

When using the T-distribution the formula is T n (Z) or T n (-Z) for lower and upper-tailed tests, respectively. T n is the cumulative distribution function for a T-distribution with n degrees of freedom and so a T-score is computed. Selecting this mode makes the tool behave as a T test calculator.

The population standard deviation is often unknown and is thus estimated from the samples, usually from the pooled samples variance. Knowing or estimating the standard deviation is a prerequisite for using a significance calculator. Note that differences in means or proportions are normally distributed according to the Central Limit Theorem (CLT) hence a Z-score is the relevant statistic for such a test.

    Why do we need a p-value?

If you are in the sciences, it is often a requirement by scientific journals. If you apply in business experiments (e.g. A/B testing) it is reported alongside confidence intervals and other estimates. However, what is the utility of p-values and by extension that of significance levels?

First, let us define the problem the p-value is intended to solve. People need to share information about the evidential strength of data that can be easily understood and easily compared between experiments. The picture below represents, albeit imperfectly, the results of two simple experiments, each ending up with the control with 10% event rate treatment group at 12% event rate.

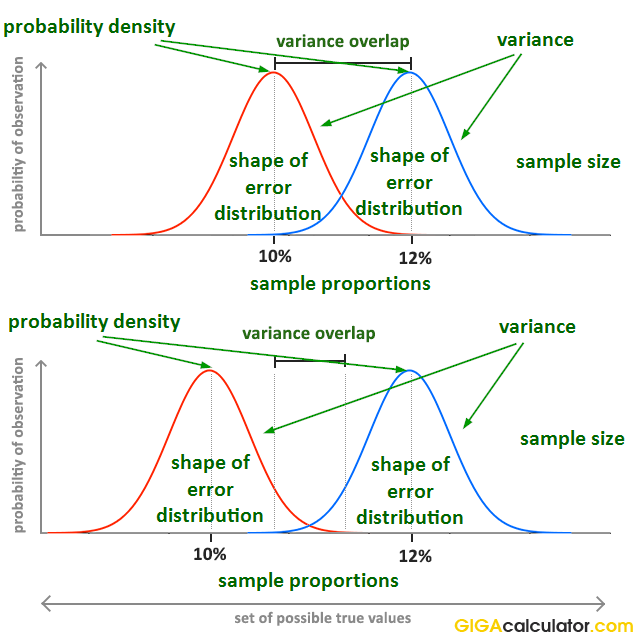
However, it is obvious that the evidential input of the data is not the same, demonstrating that communicating just the observed proportions or their difference (effect size) is not enough to estimate and communicate the evidential strength of the experiment. In order to fully describe the evidence and associated uncertainty , several statistics need to be communicated, for example, the sample size, sample proportions and the shape of the error distribution. Their interaction is not trivial to understand, so communicating them separately makes it very difficult for one to grasp what information is present in the data. What would you infer if told that the observed proportions are 0.1 and 0.12 (e.g. conversion rate of 10% and 12%), the sample sizes are 10,000 users each, and the error distribution is binomial?

Instead of communicating several statistics, a single statistic was developed that communicates all the necessary information in one piece: the p-value . A p-value was first derived in the late 18-th century by Pierre-Simon Laplace, when he observed data about a million births that showed an excess of boys, compared to girls. Using the calculation of significance he argued that the effect was real but unexplained at the time. We know this now to be true and there are several explanations for the phenomena coming from evolutionary biology. Statistical significance calculations were formally introduced in the early 20-th century by Pearson and popularized by Sir Ronald Fisher in his work, most notably "The Design of Experiments" (1935) [1] in which p-values were featured extensively. In business settings significance levels and p-values see widespread use in process control and various business experiments (such as online A/B tests, i.e. as part of conversion rate optimization, marketing optimization, etc.).

    How to interpret a statistically significant result / low p-value

Saying that a result is statistically significant means that the p-value is below the evidential threshold (significance level) decided for the statistical test before it was conducted. For example, if observing something which would only happen 1 out of 20 times if the null hypothesis is true is considered sufficient evidence to reject the null hypothesis, the threshold will be 0.05. In such case, observing a p-value of 0.025 would mean that the result is interpreted as statistically significant.

But what does that really mean? What inference can we make from seeing a result which was quite improbable if the null was true?

Observing any given low p-value can mean one of three things [3] :

• There is a true effect from the tested treatment or intervention.
• There is no true effect, but we happened to observe a rare outcome. The lower the p-value, the rarer (less likely, less probable) the outcome.
• The statistical model is invalid (does not reflect reality).

Obviously, one can't simply jump to conclusion 1.) and claim it with one hundred percent certainty, as this would go against the whole idea of the p-value and statistical significance. In order to use p-values as a part of a decision process external factors part of the experimental design process need to be considered which includes deciding on the significance level (threshold), sample size and power (power analysis), and the expected effect size, among other things. If you are happy going forward with this much (or this little) uncertainty as is indicated by the p-value calculation suggests, then you have some quantifiable guarantees related to the effect and future performance of whatever you are testing, e.g. the efficacy of a vaccine or the conversion rate of an online shopping cart.

Note that it is incorrect to state that a Z-score or a p-value obtained from any statistical significance calculator tells how likely it is that the observation is "due to chance" or conversely - how unlikely it is to observe such an outcome due to "chance alone". P-values are calculated under specified statistical models hence 'chance' can be used only in reference to that specific data generating mechanism and has a technical meaning quite different from the colloquial one. For a deeper take on the p-value meaning and interpretation, including common misinterpretations, see: definition and interpretation of the p-value in statistics .

    P-value and significance for relative difference in means or proportions

When comparing two independent groups and the variable of interest is the relative (a.k.a. relative change, relative difference, percent change, percentage difference), as opposed to the absolute difference between the two means or proportions, the standard deviation of the variable is different which compels a different way of calculating p-values [5] . The need for a different statistical test is due to the fact that in calculating relative difference involves performing an additional division by a random variable: the event rate of the control during the experiment which adds more variance to the estimation and the resulting statistical significance is usually higher (the result will be less statistically significant). What this means is that p-values from a statistical hypothesis test for absolute difference in means would nominally meet the significance level, but they will be inadequate given the statistical inference for the hypothesis at hand.

In simulations I performed the difference in p-values was about 50% of nominal: a 0.05 p-value for absolute difference corresponded to probability of about 0.075 of observing the relative difference corresponding to the observed absolute difference. Therefore, if you are using p-values calculated for absolute difference when making an inference about percentage difference, you are likely reporting error rates which are about 50% of the actual, thus significantly overstating the statistical significance of your results and underestimating the uncertainty attached to them.

In short - switching from absolute to relative difference requires a different statistical hypothesis test. With this calculator you can avoid the mistake of using the wrong test simply by indicating the inference you want to make.

    References

1 Fisher R.A. (1935) – "The Design of Experiments", Edinburgh: Oliver & Boyd

2 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

3 Georgiev G.Z. (2017) "Statistical Significance in A/B Testing – a Complete Guide", [online] https://blog.analytics-toolkit.com/2017/statistical-significance-ab-testing-complete-guide/ (accessed Apr 27, 2018)

4 Mayo D.G., Spanos A. (2006) – "Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction", British Society for the Philosophy of Science , 57:323-357

5 Georgiev G.Z. (2018) "Confidence Intervals & P-values for Percent Change / Relative Difference", [online] https://blog.analytics-toolkit.com/2018/confidence-intervals-p-values-percent-change-relative-difference/ (accessed May 20, 2018)

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "P-value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/p-value-significance-calculator.php URL [Accessed Date: 10 Apr, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

Hypothesis Testing Calculator

Understanding Hypothesis Testing: A Guide to the Hypothesis Testing Calculator

Hypothesis testing is a crucial statistical method used to make informed decisions about data and draw conclusions. Whether you’re a student, researcher, or professional, a Hypothesis Testing Calculator can be an invaluable tool in your statistical toolkit. Let’s explore what hypothesis testing is and how this calculator can assist you:

Hypothesis Testing Basics:

• Null Hypothesis (H0): This is the default assumption or claim that there is no significant difference or effect. It’s often denoted as H0.
• Alternative Hypothesis (Ha): This is the statement that contradicts the null hypothesis. It suggests that there is a significant difference or effect. It’s denoted as Ha.
• Significance Level (α): This is the predetermined threshold (e.g., 0.05 or 5%) used to determine statistical significance. If the calculated p-value is less than α, you reject the null hypothesis.
• p-value: This is the probability of observing the results (or more extreme results) if the null hypothesis is true. A small p-value suggests that the results are unlikely under the null hypothesis.

Key Features of the Hypothesis Testing Calculator:

• Input Parameters: The calculator typically requires you to input sample data, choose the type of test (e.g., t-test, chi-square test), specify the null and alternative hypotheses, and set the significance level.
• Calculations: Once you input the data and parameters, the calculator performs the necessary statistical tests and calculations. It generates results such as the test statistic, degrees of freedom, and the p-value.
• Interpretation: Based on the results, the calculator helps you determine whether to reject or fail to reject the null hypothesis. It provides an interpretation of the findings, which is crucial for drawing conclusions.
• Visual Representation: Some calculators may offer visual aids like graphs or charts to help you better understand the data distribution and test results.

Significance of the Hypothesis Testing Calculator:

• Scientific Research: Researchers across various fields use hypothesis testing to validate their hypotheses and draw meaningful conclusions from data.
• Quality Control: Industries use hypothesis testing to ensure the quality and consistency of products and processes.
• Medical Studies: In medical research, hypothesis testing helps assess the effectiveness of treatments or interventions.
• Academics: Students and educators use hypothesis testing to teach and learn statistical concepts and conduct experiments.
• Data-Driven Decisions: Businesses use hypothesis testing to make data-driven decisions, such as whether to launch a new product based on market research.

Conclusion:

The Hypothesis Testing Calculator is a powerful tool that simplifies complex statistical analysis and enables data-driven decision-making. Whether you’re conducting experiments, analyzing survey data, or performing quality control, understanding hypothesis testing and using this calculator can help you make informed choices and contribute to evidence-based research and decision-making.