visual representation of pi

Explained Visually

By Victor Powell

Before we define π, let's define a circle. A circle is a set of points that all lie an equal distance away from a single center point. The distance from the center point is called the and the distance along the outer edge of the circle is called the . The is the thickness of the circle at its widest and is 2 times the .

π is the ratio of the to the and this ratio holds true of all sizes of circles. Because of this, π is a constant and equal to approximately 3.14. But don't get hung up on the idea that the decimal number representation of 3.14 is somehow special or mystical. It could have instead been defined as the over the and in fact, this might have made more sense. (see: Tau Day .)

For more explanations, visit the Explained Visually project homepage.

Or subscribe to our mailing list.

clock This article was published more than  9 years ago

10 stunning images show the beauty hidden in pi

Saturday -- March 14, 2015, or 3/14/15 -- marks an extremely nerdy holiday. It is the official celebration of π, the magical, mathematical and infinite constant that is the ratio of a circle’s circumference to its diameter.

For any circle you can imagine, if you divide the distance around the circle by the distance across it, you will get pi, or 3.1415926535897932384626433832795028841971693993751058209749 445923078164062862089986280348253421170679821480865132823066 470938446095505822317253594081284811174502841027019385…

We could keep going, but you get the picture.

Some people will celebrate the holiday by making and eating pies (Washington restaurants are offering specials on everything from pizza to banana cream). Others will run a Pi-K race of 3.14 kilometers. And some data tinkerers are making art that visualize pi’s infinite and random digits.

One of the best known of these data tinkerers is Martin Krzywinski , a scientist who specializes in bioinformatics, or using computer science and statistics to understand biological data. Krzywinski started publishing his pi art in 2013, beginning with this visualization:

Each digit of pi is represented by a dot of a different color: 3 is orange, 1 is red, 4 is yellow, and so on. Krzywinski then folded these colored dots, each of which represents a different digit ("1" or "4"), into a spiral. Going from the center of the circle outward, here is the first 13,689 digits of pi:

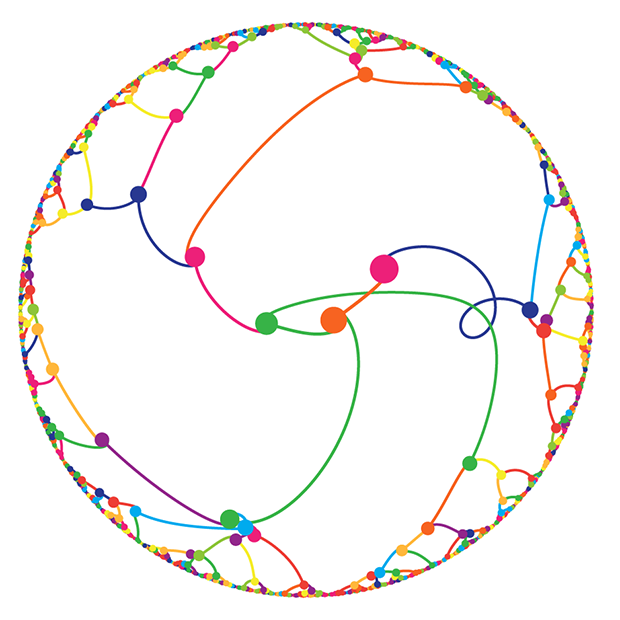
Working with Cristian Ilies Vasile, a self-described "artist by accident," Krzywinski also created a series of circular representations of pi, where the numbers are connected across the circle with a chord. The artists start at 3, draw a line to 1, draw a line to 4, and so on, changing the color with each new digit.

The image below follows the same process, except now, when a number is repeated (for example a "1," followed by another "1"), Krzywinski and Vasile place a dot at the outer edge of the circle. The more digits that are repeated, the larger the dot.

The big purple dot near the top of the circle represents a unique point in pi: A place where six 9s occur in a row. Called the Feynman Point, the repetition appears much earlier than probability would dictate.

Below is Krzywinski's new illustration for 2015, a type of diagram that is called a treemap. He first divides the box by drawing "3" lines vertically. Then he divides the first box horizontally by drawing "1" line, the second by drawing "4" lines, and so on. Here, Krzywinski randomly colored the graphic with the primary colors used by members of the De Stijl and Bauhaus art movements in the 1920s, like Piet Mondrian, Paul Klee and Joseph Albers.

So what is the point of all this? Mostly, the works are meant to be beautiful and fun to look at. But beyond that, Krzywinski says the art is meant to awaken emotions about math (hopefully emotions other than dislike and confusion) and start conversations about numbers and randomness.

"All numbers are necessarily interesting," Krzywinski says. "But, to echo the ending of Orwell's 'Animal Farm,' some numbers are more interesting than others. Pi is one of those."

Why is pi so interesting? For one thing, pi describes a perfect circle, and thus is included in any formula that describes a circle or some kind of repetition, from a heart beat to the Earth's orbit around the sun.

For another, pi has the appearance of being random (or, more accurately, "uniformly distributed") -- meaning that, as its digits continue, there is an equal chance of any digit between 0 and 9 appearing. In the first six billion digits of pi, each of the digits 0 through 9 shows up about six hundred million times .

If pi were truly random, that would mean that the number sequence in pi would never repeat itself, and -- because pi is infinite -- it would contain all patterns in existence. Any word that you can think of, when encoded in numbers, would show up in pi, says Kryzwinski. So would the entire works of Shakespeare, all possible misprints and permutations of Shakespeare, and even, if you were patient enough, pi itself. As Cornell mathematician Steven Strogatz writes for The New Yorker , pi is so special in part because it "puts infinity within reach."

Pi looks random: Mathematicians have computed pi out to 10 trillion digits and seen no evident pattern. But what really vexes mathematicians is that no one can definitely say that pi is random -- no one has figured out the mathematical proof. And in another sense, pi is anything but random: After all, the number embodies the order of a perfect circle. "The tension between order and randomness is one of the most tantalizing aspects of pi," writes Strogatz .

This randomness is illustrated in another visualization of pi created by Nadieh Bremer, an astronomer who now does data art and analytics at the blog Visual Cinnamon . Bremer says she was inspired by Krzywinski's work to create a kind of map of pi, in which each digit is assigned both a color and a direction.

Bremer notes that the idea has been around for a while: In the 1888 book “The Logic of Chance,” mathematician John Venn suggested that the digits 0 to 7 in pi represent eight compass directions, and followed the path tracked by those digits. Cristian Vasile also did a random walk using pi digits , mapping the image over the Earth's surface.

Bremer's graphics follow pi as it "walks" out 100, 1,000, 10,000, 100,000 and finally 1 million digits.

Bremer says that her favorite part about the visualization is that the shape of 1,000 digits has no obvious relationship to 10,000 digits, and seeing 10,000 digits gives you no idea how 100,000 digits will look. Bremer describes this as the epitome of randomness: What came before has no influence on what happens next, and there is no evident structure or pattern.

What else can we take away from these graphics? For one, seeing all of the digits of pi visualized in physical space should help bring home another attribute of mathematics. Math isn't just numbers on a page: From physics to architecture, math is the language that we use to describe and construct the physical world around us. That's especially true for pi, which describes a perfect circle that appears everywhere in nature.

Says Kryzwinski, "Pi Day is a great time to take a moment and recognize the extent to which, as a language to describe reality, math has allowed us to write the details of the workings of our universe."

"Thanks to numbers and math, we can build devices that will deliver this text to you. And, as you read it, we know how fast the photons will be traveling and what happens when they hit your retina. The rest is up to you."

Read more stories on data visualization:

- How a dog sees a rainbow, and 12 other images that explain how we see color

- 12 fascinating optical illusions show how color can trick the eye

- A data genius computes the ultimate American road trip

Pi Day 2018

Happy Pi Day 2013, this interactive activity will guide you through ways to find π using polygons.

Most people know the definition of PI as the ratio of the circumference of a circle to its diameter. They have probably used PI in circle problems, calculating the area using area = πr 2 or the circumference using C = 2πr or C = πd . But what of this mysterious number, is it possible to create a visual analogy. This demonstration attempts to do so by examining and manipulating a regular polygon.

This will be done in two ways firstly by considering the perimeter of a regular polygon which fits perfectly in a circle of radius one, the polygon can be opened to form a straight line and its perimeter then measured. To show how π relates to area we again use a polygon, dividing its area into triangles.

The controls

For the sake of consistency with the other activites the controls are described below. But the best way to use this activity is to follow the instructions guide in the top right hand corner

• Next button is pressed to move to the next instruction
• Previous button is pressed to move back to the previous instruction
• Focus select the part to focus and zoom in on
• Area toggle area or circumference
• Exterior angles toggle to display exterior angles
• close polygon click button to animate the polygon closing
• open polygon click button to animate opening the polygon
• Exterior Angle Adjust this slider to change the exterior angle which in effect opens or closes the original polygon
• side length Adjust this slider to change the side length
• side length Adjust this slider to change the number of sides.
• Automatic recalculate - when this button is on changing the number of sides and the two other sliders will automatically adjust the angle and length to form a regular polygon that fits perfectly in the circle.

Related Activities

If you like visual mathematics why not check out the interactive multiplication tables The inspiration for this activity actually came from playing around with the interactive fractal after setting the branches to one. The interactive polygon explorer. is better for teaching the various properties and angles of polygons.

You can follow the instructions here to guide you through the activity. Or just play around and discover for yourself. Words in blue refer to interface controls, click them to be directed to the control.

Click next to continue.

• The circle has a radius of one
• Each vertex of the polygon lies on the circle

Notice the exterior angles matches the angle slider value.

In automatic mode when you change the number of sides, the angle and side length are recalculated to maintain a regular polygon

Drag the sides slider to see

Setting the sides to six gives a hexagon

• The exterior angle is 60°
• The side length is 1
• This equals the circle radius of 1
• Can you explain why?

Now we are going to make some changes to the angle slider

Drag the slider, notice what happens to the polygon as the angle approaches zero. As well as using the slider you can click the > button to open the polygon, or < to close it.

So opening up a polygon allows us to use the ruler to measure its perimeter. For the hexagon the perimeter is six since there are six sides each of length one.

We have hidden the exterior angle, to show it again click the exterior angle button.

With twenty sides, the polygon start to resemble another shape. Open up the polygon and measure its perimeter.

Now increase the sides and observe what the happens to the perimeter.

At 100 sides our polygon is now a close approximation of a circle. The perimeter of the polygon will therefore be an approximation of the circumference of the circle.

The formula for the Circumference is

r in this case is 1 the perimeter=2π So our ruler value gives us the value of 2π

What about the area of a circle?

We can consider the polygon to be made up of lots of isosceles triangles.

Click the area button so it is on

We can do the same trick and unfold the polygon

Move the angle slider to zero

We could work out the area by adding up the area of the triangles

But lets try something else

After the animation we have a new shape, a parallelogram.

With 11 sides an odd number, the end result will be a trapezium.

But we will concentrate on the area of a parallelogram produced with an even number of sides.

The area of a parallelogram is equal to the its base length x height

To calculate the height we need trigonometry, but instead try increasing the number of sides and examine what happens to the shape.

With 100 sides the height of the parallelogram is approximately the radius of the circle or 1

So the area of the circle is equal to 1 x base-length.

1xbase-length = πr 2

r=1 so base= π

So the ruler measurement gives us the base-length which is π

Happy Pi Day 2018

How To Fathom Pi: Amazing Visual Illustrations

This visual representation was created by a 41 year old individual who suffered brain damage after being attacked  by muggers. He was kicked in the had repeatedly, and amazingly, he was left with the ability to visualize complex fractal patters, which he used to represent pi.

*It is actually represented as " π," but has become known as "pi" in popular usage.

Share This Article

More on Hard Science

DISCLAIMER(S)

Articles may contain affiliate links which enable us to share in the revenue of any purchases made.

Registration on or use of this site constitutes acceptance of our Terms of Service.

© Recurrent Ventures Inc, All Rights Reserved.

July 22, 2016

The Boundless Beauty of Pi

A mathematical value with infinite digits provides limitless inspiration for data artists

By Amanda Montañez

Nadieh Bremer

This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

On March 14th of this year, I wrote about Martin Krzywinski’s 2016 “Pi Day” visualization , in which each digit of pi was reimagined as a physical mass, governed by the laws of gravity. This was the latest in a series of pi-themed visualizations by Krzywinski , who is both a scientist and a data artist; he has come out with a new graphic for Pi Day each year since 2013, and just came out with a brand new visualization for Pi Approximation Day.

2016 Pi Day visualization by Martin Krzywinski

Evidently, I was not the only one intrigued by Krzywinski’s work. Nadieh Bremer , another scientist-turned-data-visualizer, responded in 2015 with her own pi-based graphic . In honor of Pi Approximation Day (July 22nd, also denoted as 22/7, a fraction that is about equal to pi), here are a few snapshots of Bremer’s work.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Images from “Exploring the Art Hidden in Pi” by Nadieh Bremer

The main premise here, as signified quite elegantly in the legend above the first iteration of the graphic, is that each successive digit of pi is visualized as one “step” in a different direction. The visualization becomes increasingly dense and convoluted as more digits of pi are added. And interestingly, somewhere between 1,000 and 10,000 digits, the configuration seemingly begins to mimic certain natural structures, like intricately folded proteins or crystal formations. As is so often the case when data and art come together, Bremer’s work is as surprising and complex as it is beautiful.

This story is over 5 years old.

Visualizing the infinite beauty of pi and other numbers.

Progression and transition for the first 1,000 digits of π, φ and e

Progression of the first 10,000 digits of π

Progression and transition for the first 1,000 digits of e

Progression and transition for the first 2,000 digits of e

Distribution of the first 3,422 digits of π mapped onto a red-yellow-blue Brewer palette and placed as circles on an Archimedean spiral

Distribution of the first 123,201 digits of π mapped onto a red-yellow-blue Brewer palette and placed as circles on an Archimedean spiral

ORIGINAL REPORTING ON EVERYTHING THAT MATTERS IN YOUR INBOX.

By signing up, you agree to the Terms of Use and Privacy Policy & to receive electronic communications from Vice Media Group, which may include marketing promotions, advertisements and sponsored content.

Forgot password? New user? Sign up

Existing user? Log in

Already have an account? Log in here.

• Nihar Mahajan
• Margaret Zheng
• Sravanth C.
• Department 8
• Zandra Vinegar

\(\pi\) is the ratio between a circle's circumference and diameter. That is,

\[\dfrac{\text{circumference}}{\text{diameter}}=\pi.\]

\(\pi\) is a fundamental constant in mathematics, especially in geometry , trigonometry , and calculus . The first 10 digits of \( \pi\) (sometimes written as "pi" and pronounced as "pie") are \(3.141592653...\), but any finite list of digits is an approximation of \(\pi\). This is because \( \pi\) is an irrational number \(\big(\)meaning it is not perfectly equivalent to any ratio of whole numbers, \(\frac{a}{b}\big),\) as well as a transcendental number .

Applications of \( \pi\) in Geometry

Approximating \( \pi\) using polygons, approximating \( \pi\) by statistical techniques, applications of \( \pi\) in complex numbers, trigonometry, and euler's formula, exactly defining \( \pi\) as an infinite series, exactly defining \(\pi\) as an integral, more digits.

Common geometric formulae involving \(\pi:\)

• \(\pi = \frac{C}{d}, \) where \(C\) is the circumference of a circle and \(d\) is the diameter.
• \(A = \pi r^2, \) where \(A\) is the area of a circle and \(r\) is the radius.
• \(V = \frac{4}{3}\pi r^3, \) where \(V\) is the volume of a sphere and \(r\) is the radius.
• \(SA = 4\pi r^2,\) where \(SA\) is the surface area of a sphere and \(r\) is the radius.
• \(A = \pi a b, \) where \(A\) is the area of an ellipse and \(a\) and \(b\) are the semi-minor and semi-major axes.

A circle is inscribed in a square. What is the ratio of the area of the circle to the area of the square?

By measuring the perimeter of these polygons, we can approximate the perimeter of the circle.

The perimeters of these \(n\)-gons can be obtained from regular polygons trigonometry and we can then use small-angle approximation to find the limit, \(2\pi.\)

An approximation for \(\pi\) can be derived from the perimeters of a circumscribed square and an inscribed square. Let \(P_1\) be the perimeter of the larger square, \(P_2\) the perimeter of the smaller square, and \(C\) the circumference of the circle. The circumference of the circle can then be approximated by the average of the two perimeters: \[C\approx \frac{P_1+P_2}{2}.\] If \(d\) is the diameter of the circle, then the length of a side of the larger square is also \(d\). The length of a side of the smaller square can be found using a special right triangle . This length is \(\frac{\sqrt{2}}{2}d\). Now we have \[\begin{align} P_1&=4d\\ P_2&=2\sqrt{2}d. \end{align}\] So, our approximation for the circumference is \(C\approx\big(2+\sqrt{2}\big)d\). Dividing this equation by \(d\) yields us an approximation for \(\pi:\) \[\pi\approx 2+\sqrt{2}.\] This isn't a particularly good approximation! However, better approximations can be obtained using a similar method with regular polygons with more sides.

There are many simulations and statistical techniques that can be used to approximate \(\pi\). Long before computers were invented, the French mathematicians Buffon \((1707-1788)\) and Laplace \((1749-1827)\) proposed using a stochastic simulation to estimate the value of \(π\).

"Buffon's needle" famously approximates \(\pi\) using the fact that a straight needle is equally likely to land at any angle when it is tossed onto a plane.

Suppose \(n\) needles of length 1 are dropped onto a floor with strips of wood 1 unit apart. The expected value for the number of needles which cross two strips of wood is \(\frac{2}{\pi}\cdot n.\)

The crux of the proof is the idea of breaking up each needle into small segments. Loosely speaking, linearity of expectation tells us that the expected number of times that the needle will cross between two strips of wood is proportional to the length of the needle. Thus, as a function of the length \(l,\) the expected number of crossings is \(cl\) for some constant \(c.\) However, consider a circle with diameter 1 (so circumference \(\pi\)); with probability 1, this circle will intersect exactly 2 of the wood-crossings. Hence, \(c\pi = 2,\) so \(c = \frac{2}{\pi}.\) If one is uncomfortable with the idea of a circle, consider approximating the circle by combining a bunch of very, very small linear segments. \(_\square\)

This results in an easy simulation technique for approximating \(\pi.\) Simply throw \(n\) needles on the floor, count the number of needles \(x\) which cross two strips of wood, and then \(\pi \approx \frac{2n}{x}.\) This type of simulation technique is known as a Monte Carlo simulation .

Another approximation is even simpler. Think about inscribing a circle in a square with sides of length \(2\), so that the radius \(r\) of the circle is of length \(1\).

The true area of the circle is \(\pi r^{2}=\pi\). Buffon suggested that he could estimate the area of a circle by a dropping a large number of needles (which he argued would follow a random path as they fell) in the vicinity of the square. The ratio of the number of needles with tips lying within the square to the number of needles with tips lying within the circle could then be used to estimate the area of the circle:

\[\frac { { A }_{ c } }{ { A }_{ s } } =\frac { \pi { r }^{ 2 } }{ 4{ r }^{ 2 } } \implies \pi =4\frac { { A }_{ c } }{ { A }_{ s } }.\]

The number \(\pi\) is important in trigonometry , as it provides a more natural interpretation of angles than degrees do. Specifically, radians are defined so that \(2\pi\) radians are equivalent to a full circle (in other words, \(\pi\), understood as \(\pi\) radians, is commonly equal to 180 degrees when used in trigonometry); in this way, an angle of \(\theta\) corresponds to an arc length of \(\theta \cdot r\), where \(r\) is the radius of the circle. Equivalently, radians are defined so that one radian corresponds to an arc length equal to the radius of the circle.

This also allows for easy evaluation of trigonometric functions:

This also allows complex numbers to be presented in polar coordinates , meaning that any complex number can be written in the form \(re^{i\theta}\) for some real numbers \(r\) and \(\theta\). The number \(\pi\) plays a key role in their analysis, as this complex number is equivalent to

\[re^{i\theta}=r(\cos\theta + i\sin\theta)\]

as both sides represent the same point in the complex plane . Setting \(\theta = \pi\) gives the famous identity

\[e^{i\pi} + 1 = 0.\]

It is conjectured that this is the only nontrivial relation between the numbers \(e, i,\) and \(\pi\), making this result (known as Euler's formula ) even more remarkable.

Though \(\pi\) cannot be represented as any finite series of rational numbers (as a consequence of being irrational ), there are many ways to express \(\pi\) as an infinite series. The "first," historically speaking, of these sequences was an infinite product:

\[\frac{2}{\pi} = \frac{\sqrt{2}}{2} \times \frac{\sqrt{2+\sqrt{2}}}{2} \times \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \times \cdots, \]

which, since the \(n^\text{th}\) term of the infinite product is \(\cos\frac{\pi}{2^n}\) by repeated application of the half-angle formula, is equivalent to the statement

\[\lim_{n \rightarrow \infty} \frac{1}{2^n\sin\frac{\pi}{2^{n+1}}} = \frac{2}{\pi},\]

which is true, as \(\sin\frac{\pi}{2^{n+1}}\approx \frac{\pi}{2^{n+1}}\) for large \(n\).

More useful series involves infinite sums rather than products, because calculating the first few terms of an infinite expression of \(\pi\) gives good approximations of its value. The simplest is the Gregory-Leibniz series, which uses the evaluation of the Taylor series of \(\arctan x\) at 1:

\[\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots.\]

However, this converges slowly, meaning that a large number of terms are necessary to get a good approximation of \(\pi\). Better series include Machin-like formulae:

\[\begin{align} \frac{\pi}{4} &= 4\arctan\frac{1}{5}-\arctan\frac{1}{239}\\ \frac{\pi}{4} &= 22\arctan\frac{24478}{873121}+17\arctan\frac{685601}{69049993}. \end{align}\]

In the modern computer era, even better series are known:

\[\frac{1}{\pi} = \frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{k!^4(396^{4k})},\]

which can be used to calculate millions of digits of \(\pi\).

\(\pi\) can also be defined in terms of integrals . The simplest are those that represent the area or perimeter of a circle:

\[\int_{-1}^1\sqrt{1-x^2}dx = \frac{\pi}{2},\]

as \(\left(x,\sqrt{1-x^2}\right)\) represents the top half of a circle over \([-1,1]\).

More complicated integrals come from statistics , such as the area under the normal distribution :

\[\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}\]

and the Cauchy distribution:

\[\int_{-\infty}^{\infty}\frac{1}{x^2+1}dx=\pi.\]

Finally, \(\pi\) appears in various expressions involving the gamma function , which is an extension of the factorial function defined as

\[\Gamma(t) = \int_0^{\infty}x^{t-1}e^{-x}dx,\]

which contains \(\pi\) when evaluated on half-integers. For example,

\[\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}, ~~\Gamma\left(\frac{5}{2}\right)=\frac{3}{4}\sqrt{\pi}.\]

The first 500 digits of \( \pi\) are

\(\small 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 \\ \small 8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196 \\ \small 4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273 \\ \small 7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094 \\ \small 3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912...\)

For more digits, follow the link by clicking here .

Problem Loading...

Note Loading...

Set Loading...

Draw a circle with a diameter (all the way across the circle) of 1

Then the circumference (all the way around the circle) is 3.14159265... a number known as Pi

Pi (pronounced like "pie") is often written using the greek symbol π

The definition of π is:

The Circumference divided by the Diameter of a Circle.

The circumference divided by the diameter of a circle is always π , no matter how large or small the circle is!

To help you remember what π is ... just draw this diagram.

Finding Pi Yourself

Draw a circle, or use something circular like a plate.

Measure around the edge (the circumference ):

Measure across the circle (the diameter ):

82 cm / 26 cm = 3.1538...

That is pretty close to π . Maybe if I measured more accurately?

We can use π to find a Circumference when we know the Diameter

Circumference = π × Diameter

Example: You walk around a circle which has a diameter of 100 m, how far have you walked?

Also we can use π to find a Diameter when we know the Circumference

Diameter = Circumference / π

Example: Sam measured 94 mm around the outside of a pipe ... what is its Diameter?

The radius is half of the diameter, so we can also say:

For a circle with a radius of 1

The distance half way around the circle is π = 3.14159265...

π is approximately equal to:

3.14159265358979323846…

The digits go on and on with no pattern.

π has been calculated to over 100 trillion decimal places and still there is no pattern  to the digits, see Pi Normal .

Approximation

A quick and easy approximation for π is 22/7

22/7 = 3.1428571...

But as you can see, 22/7 is not exactly right . In fact π is not equal to the ratio of any two numbers, which makes it an irrational number .

A really good approximation, better than 1 part in 10 million, is:

355/113 = 3.1415929... (think "113355", slash the middle "113/355", then flip "355/113")

Remembering The Digits

I usually just remember "3.14159", but you can also count the letters of:

"May I have a large container of butter today" 3 1 4 1 5 9 2 6 5

To 100 Decimal Places

Here is π with the first 100 decimal places:

Calculating Pi Yourself

There are many special methods used to calculate π and here is one you can try yourself: it is called the Nilakantha series (after an Indian mathematician who lived in the years 1444–1544).

It goes on for ever and has this pattern:

3 + 4 2×3×4 − 4 4×5×6 + 4 6×7×8 − 4 8×9×10 + ...

(Notice the + and − pattern, and also the pattern of numbers below the lines.)

It gives these results:

Get a calculator (or use a spreadsheet) and see if you can get better results.

Pi Day is celebrated on March 14. March is the 3rd month, so it looks like 3/14

To revisit this article, visit My Profile, then View saved stories .

• Backchannel
• Newsletters
• WIRED Insider
• WIRED Consulting

Madhumita Venkataramanan

Visual rendering of first 100 billion digits of pi proves randomness

This article was taken from the August 2013 issue of Wired magazine. Be the first to read Wired's articles in print before they're posted online, and get your hands on loads of additional content by subscribing online .

This image is a representation of the first 100 billion digits of pi. "I was interested to see what I'd get by turning a number into a picture," says mathematician Jon Borwein, from the University of Newcastle in Australia, who collaborated with programmer Fran Aragon. "We wanted to prove, with the image, that the digits of pi are really random," explains Aragon. "If they weren't, the picture would have a structure or a repeating shape, like a circle, or some broccoli."

This image is equivalent to 10,000 photos from a ten-megapixel camera, and it can be explored in Gigapan . The technique doesn't only confirm established theories -- it can also provide insights: during the drawing of a supposedly random sequence called the "Stoneham number", Aragon noticed a regularly occurring shape within the figure. "We were able to show that the Stoneham number is not random in base 6," he explains. "We would never have known this without visualising it."

Going for a random walk

Borwein and Aragon drew the image using a classic tool called the "random walk" - a path described by the sequence of digits in a random number. The rules of the walk depend on the number's base: if the base is 4, the algorithm can draw in four different directions, as they do in this figure. For 1, you go right, 2 indicates up, 3 is to the left, 0 is down.

This article was originally published by WIRED UK

Nena Farrell

Henri Robbins

Sachi Mulkey

Visualizing Pi

314 Visualizing Pi The decimal representation of Pi has been computed to more than a trillion digits (102). Pi can be estimated by dividing the circumference of any circle by its diameter. circumference 3.1415926535897932384626433832 6.4 79502884197169399375105820974 9445923078164062862089986280 Pi has about 6.4 billion known digits which would take a person roughly 133 years to recite without stopping. The world record holder for the diameter billion digits most memorized digits of Pi took nine hours to recite over 44,000 digits of Pi. Ancient Egyptian, Babylonian, Indian, and Greek mathema- The ratio of the Great Pyramid of Giza's height to perimeter comes out to approxi- mately 2pi. ticians all knew the |+l+l+l=P ratio of circumfer- ence to diameter of a circle was slightly more than 3. Pi (which is a letter in the Greek alphabet) was discovered by a Greek mathematician named Archimedes. He stated the Pi is a The earliest known reference to Pi occurs in an Egyptian papyrus scroll, written around 1650 BC by a scribe named Ahmes. number between 3 10/71 and 3 1/7. He found it by taking a polygon with 96 sides and inscribing a circle inside the polygon. That was Archimedes' concept of pi. All the digits of Pi can never be fully known. It took Yasumasa Kanada, a professor at the University of Tokyo, approximately 116 hours to compute 6,442,450,000 decimal places of Pi on a computer. The decimal rep of Pi truncated to 11 digits is accurate enough to estimate the circumference There is no zero in the first 31 digits of Pi. At 39 digits Pi can estimate the circumference of any circle within the observable universe with precision comparable to the of any circle that fits inside the earth within an error of les of a hydrogen atom. than one millimeter. 3.14159265358979323846264338327950288419716939937510582097494459230781 64062862089986280348253421170679821480865132823066470938446095505822317 2535940812848111745028410270193852110555964462294895493038196442881097566 593344612847564823378678316527120190914564856692346034861045432664821339 360726024914127372458700660631558817488152092096282925409171536436789259 03600113305305488204665213841469519415116094330572703657595919530921861173 819326117931051185480744623799627495673518857527248912279381830119491298336 733624406566430860213949463952247371907021798609437027705392171762931767 5238467481846766940513200056812714526356082778577134275778960917363717872 1468440901224953430146549585371050792279689258923542019956112129021960864 0344181598136297747713099605187072113499999983729780499510597317328160963 1859502445945534690830264252230825334468503526193118817101000313783875288 No simple base- 10 pattern in the digits of Pi has ever been found. At position 763 there are six nines in a row. This is known as 3/14 the Feynman Point. Pi day is celebrated on March 14 at the Exploratorium in San Francisco. The first to use Pi definitely to stand for the ratio of circumference to diameter was an English writer William Jones. He used it to symbolize the word "periphery." Euler adopted the symbol in 1737, and since that time it has been in general use. Circumference Area Surface Area Ttd Tre 2Trh+2JTr² 2 Pi in radians form is 360 degrees. or Volume 2Tr Trn Therefore Pi radians is 180 degrees and 1/2 Pi radians is 90 degrees. Sources: http://facts.randomhistory.com2009/07/03_pi.html http://ualr.edu/lasmoller/pi.html http://www.roma.unisa.edu.au/07305/symbols.htm#Pi Surface Area Surface Area 4TTr Trv(r²+h?)+JCr² nttp//mathforum.org/libray/dmat/view/57543html Volume Volume (4/3)TTr3 (1/3)TTrêh

You may also like...

For hosted site:

For wordpress.com:

Created during January 2015

The Art in Pi

Design blog

Get a print

Illustrator

Digits of Pi

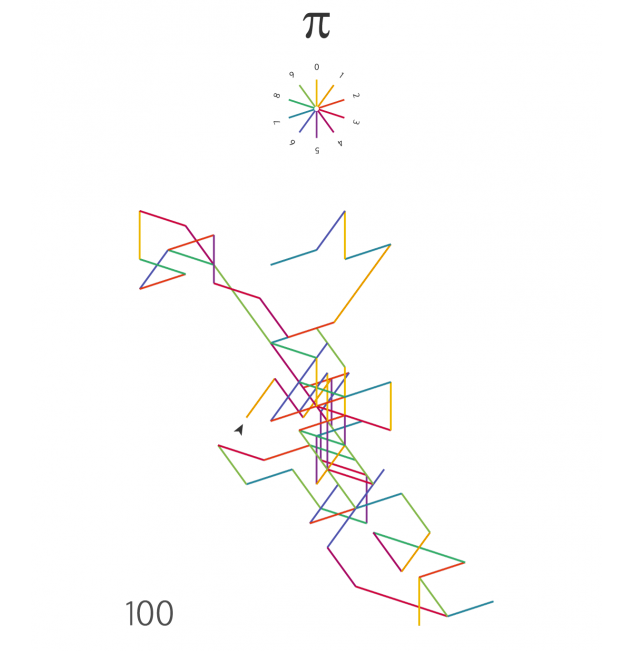
A visualization that turns the digits of the number π into a visual presentation . Each digit is converted into a certain direction to step. With 360 degrees of a circle, divided into 10 step directions. You can follow the path that the digits make and how this is always random, no matter if you look at 100, 1000, or even a million digits.

After seeing the examples of Martin Krzywinski’s π art work I wanted to venture into the world of data art myself. My idea of using the digits of π to step into a certain direction certainly isn’t new, but most versions I could find had first converted pi into another base (4 or 16 for example). Therefore, I went ahead with just keeping it in base 10. I plotted and colored the data in R and then imported the PDF into Illustrator to add some text and legends.

Read more about the data, design an creation in my blog . You can also get these visualizations as a high quality giclée print in my online shop .

Exploring the art hidden in π

Using the digits of pi to create a path across the screen that is totally driven by this never ending number

The Cosmic Surprise

Revealing more than a million galaxies observed by DESI for the Scientific American's front spread of an article celebrating 25 years since the discovery of Dark Energy

The Essence of Us

A unique data art piece that visualizes the 5000+ exoplanets discovered so far to pose the question 'What defines human culture?'

Jump to navigation

• Directory / Phonebook

Search form

Why Pi? It's a History Lesson All Its Own Last weekend marked a celebration of Super Pi Day, the single date per century that most closely resembles the legendary mathematical constant.

From the wheels that get you from Point A to Point B, to the GPS system that helps you find your way, there is a single number that makes these and countless other innovations possible.

Pi, an irrational number typically approximated as 3.14159, has proved itself as both a captivator of the imagination and an irreplaceably practical part of everyday life.

Last Saturday saw the observance of Super Pi Day, a once-in-a-century event on which the date (3/14/15) most closely corresponds to the mathematical representation of pi. Attendees at the Tucson Festival of Books on the University of Arizona campus celebrated the occasion with the Science of Pi, a brand-new addition to Science City that featured a number of activities and demonstrations designed to showcase the importance of the vaunted number.

At the Science of Pi tent, visitors used pi to design their own bouncy balls, created colorful visual representations of pi, and participated in a Buffon's Needle experiment. In the experiment, participants tossed toothpicks across a board with parallel lines. At the end of the day, the ratio of the number of sticks thrown to the number of sticks that crossed the lines was approximately 3.14, or pi.

Science of Pi volunteers also hosted a pi digit recitation contest — which took place at 3:14 p.m., of course. Austin Troike, the contest winner, accurately recited 171 digits of pi from memory.

Science City's Science Café lecture series featured Rebecca Klemm, a statistician and renowned STEM educator known popularly as the "Numbers Lady." Her talk, "The Intriguing Story of Pi," attracted audience members young and old as she explained the long history and countless uses of pi alongside a giant stuffed pi doll. On campuses elsewhere, five-kilometer (3.1-mile) races were part of the fun, some of them billed as "The Pi Mile," starting at 9:26 a.m. (for 3.1415926) and serving pie afterward.

What is it about pi that calls for such a celebration? Put simply, pi is one of the oldest and most widely used mathematical constants known to mankind.

Nearly 4,000 years ago, ancient Babylonians and Egyptians made the observation that the ratio of a circle's circumference to its diameter (C/d) was the same constant for every circle. While early estimations of this constant were inaccurate, the Babylonians and Egyptians were among the first to show that pi could be used to calculate the area of a circle.

More accurate calculations of pi came from the famous Greek philosopher Archimedes in the 200s B.C. and the Chinese mathematician Zu Chongzhi in the fifth century. Mathematicians worldwide continued to delve more deeply into the meaning of pi for the next several centuries.

In the early 1700s, mathematicians William Jones and Leonhard Euler popularized the use of the Greek letter to represent the mysterious constant. In 1767, mathematician Johann Heinrich Lambert was the first to realize that pi was irrational, meaning that it is not a terminating or repeating sequence of digits.

Not only did Lambert help to illuminate the nature of pi as we know it today, he also ensured that pi digit memorizers would always have their work cut out for them.

However, modern applications of pi extend far beyond Pi Day contests and calculating the area of circles in middle-school math class. Pi is fundamental to every science and engineering discipline in existence today.

Mechanical engineers use pi to design and build aircraft, cars and other heavy machinery. Pi is used in signal processing, which provides the basis for radio, telephones and TV. Statisticians use pi to make sense of large data sets of all kinds. And computer engineers frequently employ pi to write the programs behind the digital devices we all know and love.

Amazingly, pi also is readily found in the natural world. Pi can be used to accurately describe the geometry of the DNA double helix, found in every living being on the planet. Pi has helped astronomers accurately determine the shape of — and distances between — stars, planets and other celestial bodies. The behavior of naturally occurring waves, such as those of light or sound, can be predicted using pi. Using pi to study the shape of the eye has been invaluable in the fields of optometry and ophthalmology. Finally, pi is found in the shapes of rivers and the way they wind across a landscape.

The discovery of pi represents a monumental achievement in human history, and this year's Super Pi Day festivities provided festival participants with the perfect way to celebrate.

Resources for the media

University of Arizona in the News

Subscribe to UANow

Get the latest University of Arizona news delivered in your inbox. Or, stay in the loop using our Amazon Alexa skill.

Get Alexa alerts

Initial Thoughts

Perspectives & resources, what is high-quality mathematics instruction and why is it important.

• Page 1: The Importance of High-Quality Mathematics Instruction
• Page 2: A Standards-Based Mathematics Curriculum
• Page 3: Evidence-Based Mathematics Practices

What evidence-based mathematics practices can teachers employ?

• Page 4: Explicit, Systematic Instruction

Page 5: Visual Representations

• Page 6: Schema Instruction
• Page 7: Metacognitive Strategies
• Page 8: Effective Classroom Practices
• Page 9: References & Additional Resources
• Page 10: Credits

Research Shows

• Students who use accurate visual representations are six times more likely to correctly solve mathematics problems than are students who do not use them. However, students who use inaccurate visual representations are less likely to correctly solve mathematics problems than those who do not use visual representations at all. (Boonen, van Wesel, Jolles, & van der Schoot, 2014)
• Students with a learning disability (LD) often do not create accurate visual representations or use them strategically to solve problems. Teaching students to systematically use a visual representation to solve word problems has led to substantial improvements in math achievement for students with learning disabilities. (van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014)
• Students who use visual representations to solve word problems are more likely to solve the problems accurately. This was equally true for students who had LD, were low-achieving, or were average-achieving. (Krawec, 2014)

Visual representations are flexible; they can be used across grade levels and types of math problems. They can be used by teachers to teach mathematics facts and by students to learn mathematics content. Visual representations can take a number of forms. Click on the links below to view some of the visual representations most commonly used by teachers and students.

How does this practice align?

High-leverage practice (hlp).

• HLP15 : Provide scaffolded supports

CCSSM: Standards for Mathematical Practice

• MP1 : Make sense of problems and persevere in solving them.

Number Lines

Definition : A straight line that shows the order of and the relation between numbers.

Common Uses : addition, subtraction, counting

Strip Diagrams

Definition : A bar divided into rectangles that accurately represent quantities noted in the problem.

Common Uses : addition, fractions, proportions, ratios

Definition : Simple drawings of concrete or real items (e.g., marbles, trucks).

Common Uses : counting, addition, subtraction, multiplication, division

Graphs/Charts

Definition : Drawings that depict information using lines, shapes, and colors.

Common Uses : comparing numbers, statistics, ratios, algebra

Graphic Organizers

Definition : Visual that assists students in remembering and organizing information, as well as depicting the relationships between ideas (e.g., word webs, tables, Venn diagrams).

Common Uses : algebra, geometry

Before they can solve problems, however, students must first know what type of visual representation to create and use for a given mathematics problem. Some students—specifically, high-achieving students, gifted students—do this automatically, whereas others need to be explicitly taught how. This is especially the case for students who struggle with mathematics and those with mathematics learning disabilities. Without explicit, systematic instruction on how to create and use visual representations, these students often create visual representations that are disorganized or contain incorrect or partial information. Consider the examples below.

Elementary Example

Mrs. Aldridge ask her first-grade students to add 2 + 4 by drawing dots.

Notice that Talia gets the correct answer. However, because Colby draws his dots in haphazard fashion, he fails to count all of them and consequently arrives at the wrong solution.

High School Example

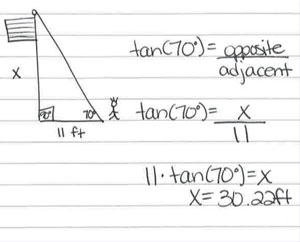
Mr. Huang asks his students to solve the following word problem:

The flagpole needs to be replaced. The school would like to replace it with the same size pole. When Juan stands 11 feet from the base of the pole, the angle of elevation from Juan’s feet to the top of the pole is 70 degrees. How tall is the pole?

Compare the drawings below created by Brody and Zoe to represent this problem. Notice that Brody drew an accurate representation and applied the correct strategy. In contrast, Zoe drew a picture with partially correct information. The 11 is in the correct place, but the 70° is not. As a result of her inaccurate representation, Zoe is unable to move forward and solve the problem. However, given an accurate representation developed by someone else, Zoe is more likely to solve the problem correctly.

Manipulatives

Some students will not be able to grasp mathematics skills and concepts using only the types of visual representations noted in the table above. Very young children and students who struggle with mathematics often require different types of visual representations known as manipulatives. These concrete, hands-on materials and objects—for example, an abacus or coins—help students to represent the mathematical idea they are trying to learn or the problem they are attempting to solve. Manipulatives can help students develop a conceptual understanding of mathematical topics. (For the purpose of this module, the term concrete objects refers to manipulatives and the term visual representations refers to schematic diagrams.)

It is important that the teacher make explicit the connection between the concrete object and the abstract concept being taught. The goal is for the student to eventually understand the concepts and procedures without the use of manipulatives. For secondary students who struggle with mathematics, teachers should show the abstract along with the concrete or visual representation and explicitly make the connection between them.

A move from concrete objects or visual representations to using abstract equations can be difficult for some students. One strategy teachers can use to help students systematically transition among concrete objects, visual representations, and abstract equations is the Concrete-Representational-Abstract (CRA) framework.

If you would like to learn more about this framework, click here.

Concrete-Representational-Abstract Framework

• Concrete —Students interact and manipulate three-dimensional objects, for example algebra tiles or other algebra manipulatives with representations of variables and units.
• Representational — Students use two-dimensional drawings to represent problems. These pictures may be presented to them by the teacher, or through the curriculum used in the class, or students may draw their own representation of the problem.
• Abstract — Students solve problems with numbers, symbols, and words without any concrete or representational assistance.

CRA is effective across all age levels and can assist students in learning concepts, procedures, and applications. When implementing each component, teachers should use explicit, systematic instruction and continually monitor student work to assess their understanding, asking them questions about their thinking and providing clarification as needed. Concrete and representational activities must reflect the actual process of solving the problem so that students are able to generalize the process to solve an abstract equation. The illustration below highlights each of these components.

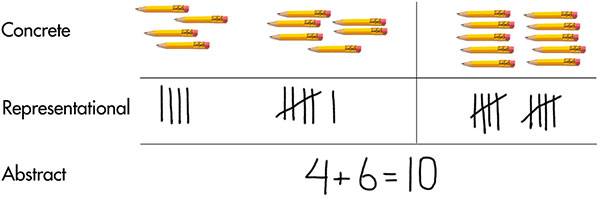
For Your Information

One promising practice for moving secondary students with mathematics difficulties or disabilities from the use of manipulatives and visual representations to the abstract equation quickly is the CRA-I strategy . In this modified version of CRA, the teacher simultaneously presents the content using concrete objects, visual representations of the concrete objects, and the abstract equation. Studies have shown that this framework is effective for teaching algebra to this population of students (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).

Kim Paulsen discusses the benefits of manipulatives and a number of things to keep in mind when using them (time: 2:35).

Kim Paulsen, EdD Associate Professor, Special Education Vanderbilt University

View Transcript

Transcript: Kim Paulsen, EdD

Manipulatives are a great way of helping kids understand conceptually. The use of manipulatives really helps students see that conceptually, and it clicks a little more with them. Some of the things, though, that we need to remember when we’re using manipulatives is that it is important to give students a little bit of free time when you’re using a new manipulative so that they can just explore with them. We need to have specific rules for how to use manipulatives, that they aren’t toys, that they really are learning materials, and how students pick them up, how they put them away, the right time to use them, and making sure that they’re not distracters while we’re actually doing the presentation part of the lesson. One of the important things is that we don’t want students to memorize the algorithm or the procedures while they’re using the manipulatives. It really is just to help them understand conceptually. That doesn’t mean that kids are automatically going to understand conceptually or be able to make that bridge between using the concrete manipulatives into them being able to solve the problems. For some kids, it is difficult to use the manipulatives. That’s not how they learn, and so we don’t want to force kids to have to use manipulatives if it’s not something that is helpful for them. So we have to remember that manipulatives are one way to think about teaching math.

I think part of the reason that some teachers don’t use them is because it takes a lot of time, it takes a lot of organization, and they also feel that students get too reliant on using manipulatives. One way to think about using manipulatives is that you do it a couple of lessons when you’re teaching a new concept, and then take those away so that students are able to do just the computation part of it. It is true we can’t walk around life with manipulatives in our hands. And I think one of the other reasons that a lot of schools or teachers don’t use manipulatives is because they’re very expensive. And so it’s very helpful if all of the teachers in the school can pool resources and have a manipulative room where teachers can go check out manipulatives so that it’s not so expensive. Teachers have to know how to use them, and that takes a lot of practice.

• Homeschooling
• World Culture
• How to Work at Home With Kids
• Managing Screen Time
• Mindful Parenting
• The Secret of Joyful Parenting
• Crochet Doll Pattern
• DIY Cardboard Crafts
• Pour Painting
• Sewing Tutorials
• Calm Down Activities
• Picture Book Activities
• Outdoor Game Day Ideas
• Play Dough Recipe
• Family Road Trip
• Tips for Long Flights With Kids
• Packing for Trips With Children
• Why Go On a Family Road Trip
• Gift Guides

Fun Ways to Celebrate Pi Day with Kids!

Fun ways to celebrate Pi Day with kid s! From eating pie to playful math to pi themed art projects, we’ve got pi activities for everyone!

Pi Day – a day set aside every year on March 14th to celebrate the mathematical constant 3.1415 (etc.) is a fun day for math geeks like me. I also think that Pi Day is a wonderful opportunity to get kids thinking about ways in which math can be fun, so today I am sharing some fun ways to celebrate Pi Day with kids – a few days early, so you have time to plan. This year it is extra special, because a sequential time will occur during Pi Day at 9:26:53 following the sequence of pi (you can also celebrate at 9:26:54 if you choose to round up).

Pi Day Activities for Kids

What You'll Find on This Page

Some links on this site are affiliate links and I may earn a small commission at no cost to you. Thank you!  Learn more .

Have you ever tried to visualize Pi? Last year my brilliant bloggy friend Erica wrote a wonderful post about creating Pi skyline art .

I thought Erica’s post was cool, but it required a lot of patience, and the image immediately reminded me of Cuisenaire rods , which happen to be one of my favorite math manipulatives.

Then I discovered these overhead projector Cuisenaire rods , and I knew they would be even more fun for my Pi Day project! This is a great affordable light table solution for a single child.

Learning Through Pi Day Play

The kids spent some time playing with the overhead Cuisenaire rods on the table, because playing with math manipulatives is one the best ways for kids to develop a mathematical instinct! Do you see how Anna is laying the foundation for understanding fractions as she plays with these little overhead pieces on our light table?

Cuisenaire rods are color coded based on how many units long they are. We used the light table Cuisenaire rods because they are a lot of fun and they photograph beautifully, but the wooden or plastic ones work equally well and are the same colors and length. The white squares represent one unit, red two, lime green three, magenta four, yellow five, green six, brown 7, red eight, and blue nine. We didn’t need the orange ten unit piece for this project.

You can read the first 23 digits of pi on our light table in the image above (or the identical one at the top of this post): 3.1415926535897932384626. Want more digits? You can find the first 10,000 digits here . That should keep you (or the kids) busy for a while!

Pi Day Activities, Art, Books, and Food!

Here are more fun ways to celebrate Pi Day with your kids!

• Decorate a Pi Tree  – free printable
• R ead Sir Cumference and the Dragon of Pi
• Bake a Pi – in a Pi-shaped pan ! This Apple Pi Pie is also fun!
• Investigating Pi for Preschoolers
• Draw a Pi Skyline – in case you missed my earlier link to the inspiration for this project.
• Preschool Pi Day Math Fun – with a pie
• Make a Pi Day poster
• Introduction to Pi – a simple visual activity

How are you going to celebrate Pi Day this year?

Share comments and feedback below, on  my Facebook page , or by  tagging me on Instagram .  Sign up for my newsletter  to receive book recommendations, crafts, activities, and parenting tips in your inbox every week.

MaryAnne Kochenderfer

MaryAnne is a craft loving educator, musician, photographer, and writer who lives in Silicon Valley with her husband Mike and their four children.

12 thoughts on “Fun Ways to Celebrate Pi Day with Kids!”

I always forget about this day every year. I love that you celebrate and make it fun!

I love your Pi Day ideas. My son especially loves the Sir Cumference series.

This is a clever take on the Pi skyline activity!! So beautiful on the light table.

Love this activity! I might ask daughter today how she wants to celebrate PI.

That is one complicated number! I used pi a lot for work as a product designer for calculate circumferences and model making. I love the look of your “skyline” and I love that you could see Anna making sense of fractions!

This is a GREAT project and you are right, requires much less patience than our project. My son has an unusual amount of patience for tedious activities (well, my older son anyway!) but this is very doable!

I love your take on the Pi Skyline.

I love Pi day!! This year, we’re doing a Pi-rate treasure hunt. I’ll give a treasure map to the kiddos and let them have fun. The questions will be at marked locations on the map, but helpful clues will be hidden near the questions if they are stuck. I even came up with some questions for the participating parents :-D. I was so excited that it was hard for me to get to sleep last night.

Your Pi-rate party sounds like it will be a lot of fun!

Pi Day is a great way to celebrate math. You have so many fun ways to explore Pi here. Thanks for sharing!

Love all these ideas. Not surprising as a maths geek too. Took a moment to realise our Pi day in the UK is different from yours. Due to date format, so I’ll need to store these ideas away for a bit longer. Thanks for sharing.

Ooh, that gives us a chance to celebrate all over again!

I’ve seen the Pi skyline floating around on FB, and hadn’t really looked at it beyond thinking “That looks really cool.” My kids would love this with their math blocks.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Processing for Pi

Visual synthesizer, introduction.

Integrating low cost hardware components with Processing software paves the way for creating compelling human-computer interactions. Processing’s ease of use to create visual representations and Raspberry Pi’s established ecosystem make this combination a perfect match for education, arts and science.

The visual synthesizer (synth) project aims to introduce you to combining interactive features of Processing with access to the physical world through the input / output capacity of the Raspberry Pi and a few additional hardware components.

In this project, a few physical buttons are connected to a Raspberry Pi. A person pressing these buttons can control the following parameters of objects inside of a Processing sketch that’s running on the Pi:

Depending on which buttons are pressed, various object parameters will be affected, as demonstrated in the video of the final sketch of this tutorial:

Video of the visual synth sketch running on Raspberry Pi:

By following the steps below you will get an overall understanding of how to use Raspberry Pi and Processing together to create an interactive experience. Using this knowledge, you could create more complex interactive systems or modify your existing Processing sketches to work with simple hardware described in this tutorial.

Depending on your experience with hardware, following this tutorial might require looking up some terms and concepts. If you can’t find the answers, please don’t be afraid to ask questions on the Processing Forum .

Concepts covered

The projects touches upon the following concepts:

• Making breadboard prototypes
• Accessing General Purpose Input/Output (GPIO) pins of the Raspberry Pi using Processing’s Hardware I/O library
• Using push buttons with Processing

Getting started

In order to get started, you would need a Raspberry Pi with Processing installed . The code shown in this tutorial needs to run within Processing Development Environment on the Raspberry Pi in order to work with the hardware pins of the Pi. The tutorial is written for users with various technical backgrounds so please keep that in mind as you replicate the project.

To run sketches from this tutorial, you must have Processing for ARM version 3.3.7.1 or greater.

With that, let’s gather the components and get coding!

Project Materials

In order to complete this tutorial, you would need the following items:

• a Raspberry Pi model 3+, 3 or 2 (those are recommended, it will work the Pi Zero and older versions, albeit much more slowly) with Processing installed
• TV or any screen / monitor with HDMI input
• 1-5 push buttons

History and Background information

An optional introduction to buttons.

For almost two hundred years, buttons have been one of the most commonly used methods of interfacing with technology. The underlying principle of a button is simple and well-suited for anything where there’s electricity present: completing or breaking a circuit when the button is pressed. Thanks to this functional simplicity, use of buttons as interaction method gained wide popularity. They’ve been used to do mundane and great things alike: from making it possible to type up Morse code via telegraph in the early 1800’s, ringing household bells in early 1900’s, switching TV channels in 1950’s, to launching huge rockets into space!

Nowadays we encounter buttons dozens or hundreds of times a day, sometimes without realizing it. Pressing a button is usually followed by some kind of feedback mechanism: a sound, changing light, message on a screen, etc. We often take this interaction for granted and are surprised when pushing a button doesn’t produce any sort of feedback or response.

An optional introduction to synthesizers.

A synthesizer is an electronic instrument producing a variety of sounds by generating and combining signals of different frequencies.

Synthesizers usually have a number of keys, buttons, knobs and/or sliders that affect some parameters of the sound or trigger some changes in the synthesizer’s settings.

One of the earliest synthesizers is “Musical Telegraph” invented by Elisha Gray in 1874. After gaining wide spread popularity in 1960s within pop music industry, many artists started to use synthesizers to express creativity.

In this project we will leverage the physical feeling or pressing a button and the drawing capacity of Processing to make an unusual synthesizer: a visual synthesizer.

Types of buttons

There are few different types of buttons out there, with these two being the most commonly used:

• Push buttons (also called “Momentary push buttons” or “Momentary switches”)
• Microswitches

Within these types, the connections inside the buttons could be:

• Normally Closed
• Normally Open

In this tutorial, we’ll be using the most common type of button: Normally Open Push Buttons.

Raspberry Pi GPIO and Processing

Modern Raspberry Pi computers have 26 pins that can be designated to be an input (receiving signals) or output (sending signals) pins. 9 of those are shared between other interfaces (I2C, SPI, UART), leaving 17 pins that can be used purely for input and output. Here’s a diagram showing the GPIO pins that are not shared with other interfaces on the Raspberry Pi:

GPIO stands for “General Purpose Input-Output”. Please see this page for more information about GPIO pins and their usage.

Processing’s built in Hardware I/O Library ( processing.io.* ) can work with any of the GPIO pins to read signals or output signals on those pins.

Before using the GPIO pins in your sketch, you must determine whether the pin will be used as an input (e.g. reading button state) or as an output (e.g. turning on an LED) and configure the pin by using Hardware I/O library’s GPIO.pinMode function ( reference ). When the pin is set as an input, there are three different options for it’s pinMode to choose from:

• INPUT_PULLDOWN
• INPUT_PULLUP

Using one of these three options determines whether a pull-up / pull-down resistor is enabled on that particular pin or if the default state of the circuitry of the Raspberry Pi should be used, which is not recommended.

Pull-up and pull-down resistors

Raspberry Pi has configurable pull-up and pull-down resistors on every GPIO pin. Without making use of these internal resistors, you would have to use additional resistors in order to read the state of a pin reliably.

After the pin is configured to act as an input with a pull-down or pull-up resistor, we can get the current state of the button in Processing by using digitalRead function. Here is an example using a built-in pull-up resistor and retrieving the state of the button:

If we used a pull-down resistor, the button would need to be connected to +3.3V instead of one of the ground pins, and the Processing sketch would be as follows:

With these basics covered, let’s move on!

Making the visual synth

Now that you know about different types of buttons, some basics about GPIO and Processing’s pinMode function, there are two main steps to make the visual synth:

• Make a single button change an object’s attribute within Processing
• Add more buttons and add more attributes that can be changed

Let’s start by connecting a single button to the Raspberry Pi and making it work with Processing!

Getting a single button to interact with Processing

The easiest way to make a button work on Raspberry Pi is to connect it between a GPIO pin and one of the ground pins. In order for this to register as an input when the button is pressed, an internal pull-up resistor has to be enabled.

In this tutorial, we’ll be using the INPUT_PULLUP mode for the input pins and this way avoid using other components like external resistors.

Let’s connect a single button to GPIO pin #4 and ground as shown in the schematic:

With this simple electrical circuit in place, we can create a basic sketch in Processing that will use the state of the button as the input. In this sketch, let’s fill in a circle when the button is pressed, and let’s make the circle empty when it’s not:

The Processing sketch for this basic interaction comes with the built-in examples of the Hardware I/O library and is presented below:

We can use this simple circuit and the sketch as the basis for the next steps in making the visual synth!

Our goal is to make something within Processing to react to the state of the button continuously. When the button is not pressed, we want the object to remain the same, but when the button is pressed, we’d like the object to continuously react for the entire time the button is pressed. For example, if the button is pressed, the object can expand, shrink and do that over and over until the button is released. Here’s a diagram that shows those two different stages:

To achieve this cyclical growing/shrinking animation cycle, we can use the concept of “oscillator” that comes from audio synthesizers.

From Wikipedia : “An electronic oscillator is an electronic circuit that produces a periodic, oscillating electronic signal, often a sine wave or a square wave”

The base for our oscillator will be a sinusoidal wave created with Processing sin(x) function . We can create an internal counter that will be incremented only when the button is pressed and feed the value of that counter to the sin(x) function:

Let’s try this out in practice and make a simple sketch demonstrating the cyclical growing and shrinking during button press:

When running this sketch, you should see a circle that’s only growing and shrinking when the button connected to pin 4 is pressed! Now that we have the concept of oscillator figured out and working, let’s move on to the next step and tie everything together!

Adding more buttons

Since we have one type of attribute change working, why not add more interesting object modifiers? You can explore other use cases for the oscillator, but we thought that these modifiers would demonstrate the synth capabilities well:

• Speed of changes

The same way as we connected a single button, we can connect many more buttons (a total of 26 can be connected) to the GPIO pins. For the synth we only need 5 in total, so let’s connect them to the following GPIO pins and ground:

The connection diagram is presented below:

With this connection in place, let’s test all of our buttons first by simply printing some text in the console:

If the buttons are working, you are ready to finish putting the synth together!

Having trouble? If the sketch is not responding to the button presses, please make sure that the buttons are connected between the designated pins and one of the ground (negative) pins of the Raspberry Pi.

Complete Sketch

For the final sketch, we’ll create an object “Circle” with attributes and parameters that will be affected by the buttons. When any of the buttons are pressed, an internal counter will be incremented, leading to a change in sin() values that will then increase / decrease one of the circle’s attributes. The sketch below implements the visual synth functionality:

When running this sketch, you should see the properties of the circle change whenever you press any or all buttons!

We hope you enjoyed making the visual synth and enjoy playing with it!

There are many things you could do now to take this project forward. Here are some ideas:

• Make a nice box and put this whole system in it
• Add synth-like functionality to any of your other Processing projects
• Add more buttons and make them do more things (take a picture, add more objects, etc)

Here are some additional resources about GPIO and Raspberry Pi:

• Complete Pinout for the Raspberry Pi: https://pinout.xyz