problem solving framework in mathematics

The internet browser you are using is not supported by this website. Please upgrade your browser to improve your experience.

Explore the main sections below, click on the interactive framework components, or download the full PISA 2022 Mathematics Framework Draft in PDF format.

The PISA 2022 mathematics framework defines the theoretical underpinnings of the PISA mathematics assessment based on the fundamental concept of mathematical literacy, relating mathematical reasoning and three processes of the problem-solving (mathematical modelling) cycle. The framework describes how mathematical content knowledge is organized into four content categories. It also describes four categories of contexts in which students will face mathematical challenges.

The PISA assessment measures how effectively countries are preparing students to use mathematics in every aspect of their personal, civic, and professional lives, as part of their constructive, engaged, and reflective 21 st Century citizenship.

• What is Mathematical Literacy?

Mathematical literacy is an individual’s capacity to reason mathematically and to formulate, employ, and interpret mathematics to solve problems in a variety of real-world contexts. It includes concepts, procedures, facts, and tools to describe, explain, and predict phenomena. It helps individuals know the role that mathematics plays in the world and make the well-founded judgments and decisions needed by constructive, engaged and reflective 21 st Century citizens.

• What's new in PISA 2022

PISA 2022 aims to consider mathematics in a rapidly changing world driven by new technologies and trends in which citizens are creative and engaged, making non-routine judgments for themselves and the society in which they live. This brings into focus the ability to reason mathematically, which has always been a part of the PISA framework. This technology change is also creating the need for students to understand those computational thinking concepts that are part of mathematical literacy. Finally, the framework recognizes that improved computer-based assessment is available to most students within PISA.

Mathematical Reasoning

The ability to reason logically and present arguments in honest and convincing ways is a skill that is becoming increasingly important in today’s world. Mathematics is a science about well-defined objects and notions that can be analyzed and transformed in different ways using “mathematical reasoning” to obtain certain and timeless conclusions.

In mathematics, students learn that, with proper reasoning and assumptions, they can arrive at results that they can fully trust to be true in a wide variety of real-life contexts. It is also important that these conclusions are impartial, without any need for validation by an external authority.

• The Key Understandings

At least six key understandings provide structure and support to mathematical reasoning. These key understandings include:

• understanding quantity, number systems and their algebraic properties;
• appreciating the power of abstraction and symbolic representation;
• seeing mathematical structures and their regularities;
• recognizing functional relationships between quantities;
• using mathematical modelling as a lens onto the real world(e.g., those arising in the physical, biological, social, economic and behavioural sciences);and
• understanding variation as the heart of statistics.

Use the arrows below to review the key understandings in-depth

QUANTITY, NUMBER SYSTEMS AND THEIR ALGEBRAIC PROPERTIES

This fundamental and ancient concept of quantity is conceptualized in mathematics by the concept of number systems and the basic algebraic properties that these systems employ. The overwhelming universality of those systems makes them essential for mathematical literacy.

It is also important to understand matters of representation(as symbols involving numerals, as points on a number line, or as geometric quantities) and how to move between them;the ways in which these representations are affected by number systems;and the ways in which algebraic properties of these systems are relevant for operating within the systems.

MATHEMATICS AS A SYSTEM BASED ON ABSTRACTION AND SYMBOLIC REPRESENTATION

The fundamental ideas of mathematics have arisen from human experience in the world and the need to provide coherence, order, and predictability to that experience. Many mathematical objects model reality, or at least reflect aspects of reality in some way. Abstraction involves deliberately and selectively attending to structural similarities between objects and constructing relationships between those objects based on these similarities. In school mathematics, abstraction forms relationships between concrete objects, symbolic representations, and operations including algorithms and mental models.

Students use representations– whether symbolic, graphical, numerical or geometric– to organize and communicate their mathematical thinking. Representations can condense mathematical meanings and processes into efficient algorithms. Representations are also a core element of mathematical modelling, allowing students to abstract a simplified or idealized formulation of a real - life problem.

MATHEMATICAL STRUCTURES AND THEIR REGULARITIES

Structure is intimately related to symbolic representation. The use of symbols is powerful, but only if they retain meaning for the symbolizer, rather than becoming meaningless objects to be rearranged on a page. Seeing structure is a way of finding and remembering the meaning of an abstract representation. Being able to see structure is an important conceptual aid to purely procedural knowledge.

A robust sense of mathematical structure also supports modelling.When the objects under study are not abstract mathematical objects, but rather objects from the real world to be modelled by mathematics, then mathematical structure can guide the modelling.Students can also impose structure on non - mathematical objects in order to make them subject to mathematical analysis.

FUNCTIONAL RELATIONSHIPS BETWEEN QUANTITIES

Relationships between quantities can be expressed with equations, graphs, tables, or verbal descriptions. An important step in learning is to extract from these the notion of a function itself, as an abstract object of which these are representations.

The two views of a function– the naïve view as a process and the more abstract view as an object– can be reconciled in the graph of the function. But reading a graph, coordinating the values on the axes, also has a dynamic or process aspect. And the graph of a function is an important tool for exploring the notion of a rate of change.The graph provides a visual tool for understanding a function as a relationship between co - varying quantities.

MATHEMATICAL MODELLING AS A LENS ONTO THE REAL WORLD

Variation at the heart of statistics.

Living things as well as non-living things vary with respect to many characteristics. As a result of that typically large variation, it is difficult to make generalizations in such a world without characterizing in some way to what extent that generalization holds. Accounting for variability is one, if not the central, defining element around which the discipline of statistics is based. In today’s world, people often deal with these types of situations by merely ignoring the variation. As a result, they suggest sweeping generalizations that are often misleading, if not wrong, and therefore very dangerous. Bias in the social science sense is usually created by not accounting for the variability in the trait under discussion.

Statistics is in many ways a search for patterns in a highly variable context: trying to find the signal defining“ truth” in the midst of a great deal of random noise.“Truth” is set in quotes because it is not the platonic truth that mathematics can deliver but an estimate of truth set in a probabilistic context, accompanied by an estimate of the error contained in the process.Ultimately, the decision - maker is left with the dilemma of never knowing for certain what the truth is.The estimate in the end is a set of plausible values.

The word formulate in the mathematical literacy definition refers to the ability of individuals to recognize and identify opportunities to use mathematics and then provide mathematical structure to a problem presented in some contextualized form. In the process of formulating situations mathematically, individuals determine where they can extract the essential mathematics to analyze, set up, and solve the problem. They translate from a real-world setting to the domain of mathematics and provide the real-world problem with mathematical structure, representations, and specificity. They reason about and make sense of constraints and assumptions in the problem. Specifically, this process of formulating situations mathematically includes activities such as the following:

• selecting an appropriate model from a list; **
• identifying the mathematical aspects of a problem situated in a real - life context and identifying the significant variables;
• recognizing mathematical structure(including regularities, relationships, and patterns) in problems or situations;
• simplifying a situation or problem in order to make it amenable to mathematical analysis;
• identifying constraints and assumptions behind any mathematical modelling and simplifications gleaned from the context;
• representing a situation mathematically, using appropriate variables, symbols, diagrams, and standard models;
• representing a problem in a different way, including organizing it according to mathematical concepts and making appropriate assumptions;
• understanding and explaining the relationships between the context - specific language of a problem and the symbolic and formal language needed to represent it mathematically;
• translating a problem into mathematical language or a representation;
• recognizing aspects of a problem that correspond with known problems or mathematical concepts, facts or procedures;
• using technology(such as a spreadsheet or the list facility on a graphing calculator) to portray a mathematical relationship inherent in a contextualized problem;and
• creating an ordered series of (step - by - step) instructions for solving problems.

** ** This activity is included in the list to foreground the need for the test - item developers to include items that are accessible to students at the lower end of the performance scale.

The word employ in the mathematical literacy definition refers to the ability of individuals to apply mathematical concepts, facts, procedures, and reasoning to solve mathematically formulated problems to obtain mathematical conclusions. In the process of employing mathematical concepts, facts, procedures, and reasoning to solve problems, individuals perform the mathematical procedures needed to derive results and find a mathematical solution. They work on a model of the problem situation, establish regularities, identify connections between mathematical entities, and create mathematical arguments. Specifically, this process of employing mathematical concepts, facts, procedures, and reasoning includes activities such as:

• performing a simple calculation; **
• drawing a simple conclusion; **
• selecting an appropriate strategy from a list; **
• devising and implementing strategies for finding mathematical solutions;
• using mathematical tools, including technology, to help find exact or approximate solutions;
• applying mathematical facts, rules, algorithms, and structures when finding solutions;
• manipulating numbers, graphical and statistical data and information, algebraic expressions and equations, and geometric representations;
• making mathematical diagrams, graphs, and constructions and extracting mathematical information from them;
• using and switching between different representations in the process of finding solutions;
• making generalizations based on the results of applying mathematical procedures to find solutions;
• evaluating the significance of observed(or proposed) patterns and regularities in data.

** These activities are included in the list to foreground the need for the test - item developers to include items that are accessible to students at the lower end of the performance scale.

• Interpret and Evaluate

The word interpret (and evaluate) used in the mathematical literacy definition focuses on the ability of individuals to reflect upon mathematical solutions, results, or conclusions and interpret them in the context of the real-life problem that initiated the process. This involves translating mathematical solutions or reasoning back into the context of the problem and determining whether the results are reasonable and make sense in the context of the problem.

Specifically, this process of interpreting, applying, and evaluating mathematical outcomes includes activities such as the following:

• interpreting information presented in graphical form and / or diagrams; **
• evaluating a mathematical outcome in terms of the context; **
• interpreting a mathematical result back into the real - world context;
• evaluating the reasonableness of a mathematical solution in the context of a real - world problem;
• understanding how the real world impacts the outcomes and calculations of a mathematical procedure or model in order to make contextual judgments about how the results should be adjusted or applied;
• explaining why a mathematical result or conclusion does or does not make sense given the context of a problem;
• understanding the extent and limits of mathematical concepts and mathematical solutions;
• critiquing and identifying the limits of the model used to solve a problem;and
• using mathematical thinking and computational thinking to make predictions, to provide evidence for arguments, and to test and compare proposed solutions.

** This activity is included in the list to foreground the need for the test - item developers to include items that are accessible to students at the lower end of the performance scale.

Content Knowledge

An understanding of mathematical content – and the ability to apply that knowledge to solving meaningful contextualized problems – is important for citizens in the modern world. That is, to reason mathematically and to solve problems and interpret situations in personal, occupational, societal, and scientific contexts, individuals need to draw upon certain mathematical knowledge and understanding.

The following content categories used in PISA since 2012 are again used in PISA 2022 to reflect the mathematical phenomena that underlie broad classes of problems, the general structure of mathematics and the major strands of typical school curricula:

• change and relationships;
• space and shape;
• quantity; and
• uncertainty and data.

Four topics have been identified for special emphasis in the PISA 2022 assessment. These topics are not new to the mathematics content categories. Instead, these are topics that deserve special emphasis:

• growth phenomena (change and relationships);
• geometric approximation (space and shape);
• computer simulations (quantity); and
• conditional decision making (uncertainty and data).

The notion of quantity may be the most pervasive and essential mathematical aspect of engaging with and functioning in our world. It incorporates the quantification of attributes of objects, relationships, situations, and entities in the world; understanding various representations of those quantifications; and judging interpretations and arguments based on quantity. To engage with the quantification of the world involves understanding measurements, counts, magnitudes, units, indicators, relative size, and numerical trends and patterns.

Quantification is a primary method for describing and measuring a vast set of attributes of aspects of the world. It allows for the modelling of situations, for the examination of change and relationships, for the description and manipulation of space and shape, for organizing and interpreting data, and for the measurement and assessment of uncertainty.

Computer simulations

Both mathematics and statistics involve problems that are not so easily addressed because the required mathematics is complex or involves a large number of factors all operating in the same system. Increasingly in today’s world, such problems are being approached using computer simulations driven by algorithmic mathematics.

Identifying computer simulations as a focal point of the quantity content category signals that, in the context of the computer-based assessment of mathematics, there is a broad category of complex problems. For example, students can use computer simulations to analyze budgeting and planning as part of the test item.

• Uncertainty and Data

In science, technology, and everyday life, uncertainty is a given. Uncertainty is therefore a phenomenon at the heart of the mathematical analysis of many problem situations, and the theory of probability and statistics as well as techniques of data representation and description have been established to deal with it. The uncertainty and data content category includes recognizing the place of variation in processes, having a sense of the quantification of that variation, acknowledging uncertainty and error in measurement, and knowing about chance. It also includes forming, interpreting, and evaluating conclusions drawn in situations where uncertainty is central. Quantification is a primary method for describing and measuring a vast set of attributes of aspects of the world.

Conditional decision-making

Identifying conditional decision-making as a focal point of the uncertainty and data content category signals that students should be expected to appreciate how the assumptions made in setting up a model affect the conclusions that can be drawn and that different assumptions/relationships may well result in a different conclusion.

• Change and Relationships

The natural and designed worlds display a multitude of temporary and permanent relationships among objects and circumstances, where changes occur within systems of interrelated objects or in circumstances where the elements influence one another. In many cases, these changes occur over time. In other cases, changes in one object or quantity are related to changes in another. Some of these situations involve discrete change; others involve continuous change. Some relationships are of a permanent, or invariant, nature. Being more literate about change and relationships involves understanding fundamental types of change and recognizing when they occur in order to use suitable mathematical models to describe and predict change. Mathematically, this means modelling the change and the relationships with appropriate functions and equations, as well as creating, interpreting, and translating among symbolic and graphical representations of relationships.

Growth phenomena

Understanding the dangers of flu pandemics and bacterial outbreaks, as well as the threat of climate change, demands that people not only think in terms of linear relationships but recognize that such phenomena need non-linear models reflecting a very rapid growth. Linear relationships are common and easy to recognize and understand, but to assume linearity can sometimes be dangerous.

Identifying growth phenomena as a focal point of the change and relationships content category does not signal an expectation that participating students should have studied the exponential function, and certainly the items will not require knowledge of the exponential function. Instead, the expectation is that there will be items that expect students to recognize (a) that not all growth is linear and (b) that non-linear growth has profound implications on how we understand certain situations.

• Space and Shape

Space and shape encompass a wide range of phenomena that are encountered everywhere in our visual and physical world: patterns, properties of objects, positions and orientations, representations of objects, decoding and encoding of visual information, and navigation and dynamic interaction with real shapes as well as with representations. Geometry serves as an essential foundation for space and shape, but the category extends beyond traditional geometry in content, meaning, and method, drawing on elements of other mathematical areas such as spatial visualization, measurement, and algebra.

Geometric approximation

Today’s world is full of shapes that do not follow typical patterns of evenness or symmetry. Because simple formulas do not deal with irregularity, it has become more difficult to understand what we see and to find the area or volume of the resulting structures.

Identifying geometric approximations as a focal point of the space and shape content category signals the need for students to be able use their understanding of traditional space and shape phenomena in a range of atypical situations.

An important aspect of mathematical literacy is that mathematics is used to solve a problem set in a context. The context is the aspect of an individual’s world in which the problems are placed. The choice of appropriate mathematical strategies and representations is often dependent on the context in which a problem arises. For PISA, it is important that a wide variety of contexts are used.

Problems classified in the personal context category focus on activities of one’s self, one’s family, or one’s peer group. Personal contexts include (but are not limited to) those involving food preparation, shopping, games, personal health, personal transportation, sports, travel, personal scheduling, and personal finance.

Occupational

Problems classified in the occupational context category are centred on the world of work. Items categorized as occupational may involve (but are not limited to) such things as measuring, costing, and ordering materials for building, payroll/accounting, quality control, scheduling/inventory, design/architecture, and job-related decision-making. Occupational contexts may relate to any level of the workforce, from unskilled work to the highest levels of professional work, although items in the PISA survey must be accessible to 15 - year - old students.

Problems classified in the societal context category focus on one’s community (whether local, national, or global). They may involve (but are not limited to) such things as voting systems, public transport, government, public policies, demographics, advertising, national statistics, and economics. Although individuals are involved in all of these things in a personal way, in the societal context category, the focus of problems is on the community perspective.

Problems classified in the scientific category relate to the application of mathematics to the natural world and issues and topics related to science and technology. Particular contexts might include (but are not limited to) such areas as weather or climate, ecology, medicine, space science, genetics, measurement, and the world of mathematics itself. Items that are intra-mathematical, where all the elements involved belong in the world of mathematics, fall within the scientific context.

21 st Century Skills

• critical thinking;
• creativity;
• research and inquiry;
• self - direction, initiative, and persistence;
• information use;
• systems thinking;
• communication;and
• reflection.

Although test - item developers recognize these 21 st Century skills, the mathematics items in PISA 2022 are not specifically developed according to these skills.

Below are some example exercises from the PISA 2022 Mathematics assessment. Each button below opens an overlay that shows an example experience from the application.

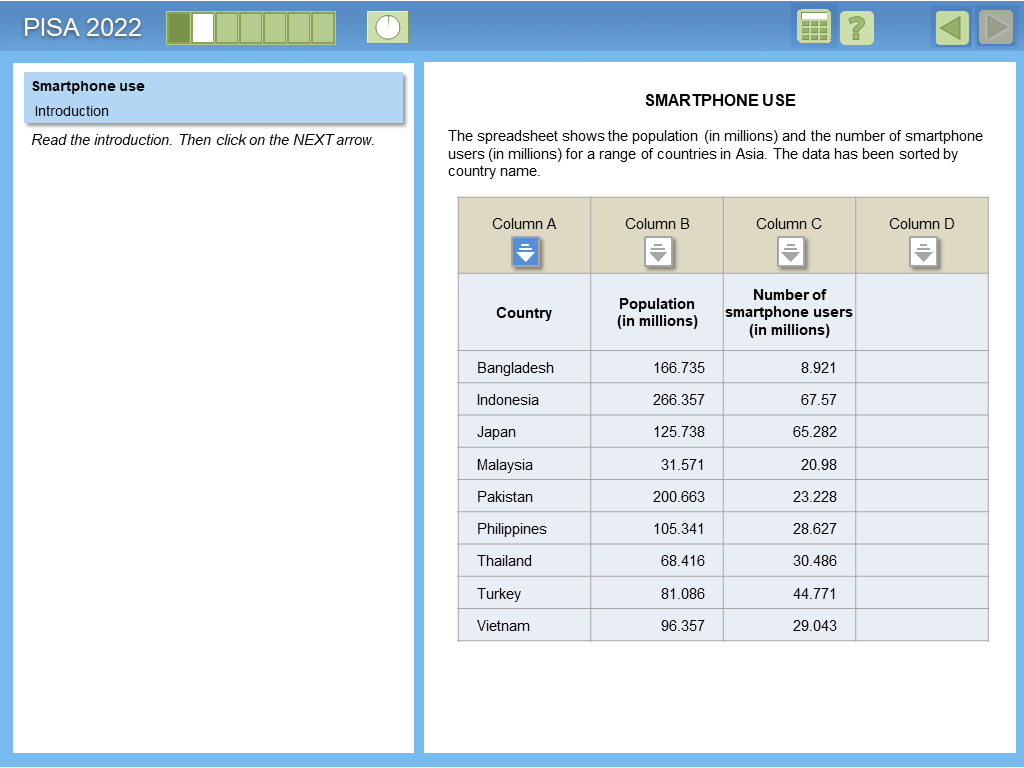
Example 1: Smartphone Use

This item illustrates computer-based assessment of mathematics (CBAM) capabilities in particular the use of spreadsheets with sorting and other capabilities.

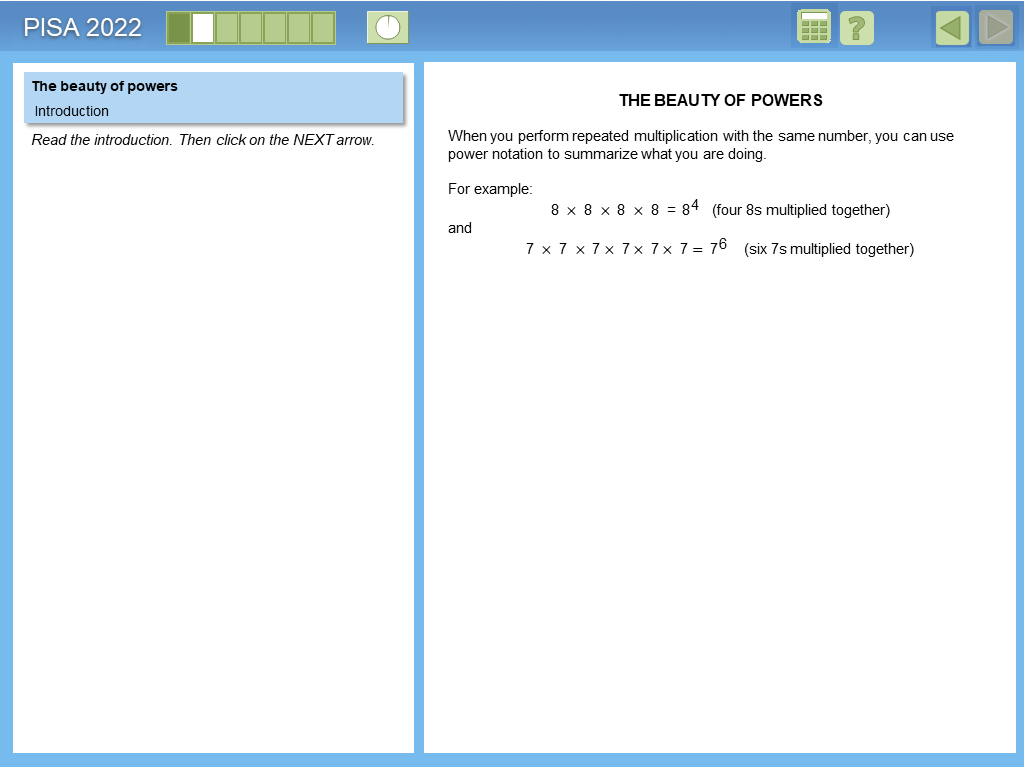
Example 2: The Beauty of Powers

This item illustrates a range of mathematics reasoning items from simple to more complex in a mathematical context and hints at growth phenomena, although, in fairness, the context for this item is more focused on reasoning and pattern recognition than it is on growth.

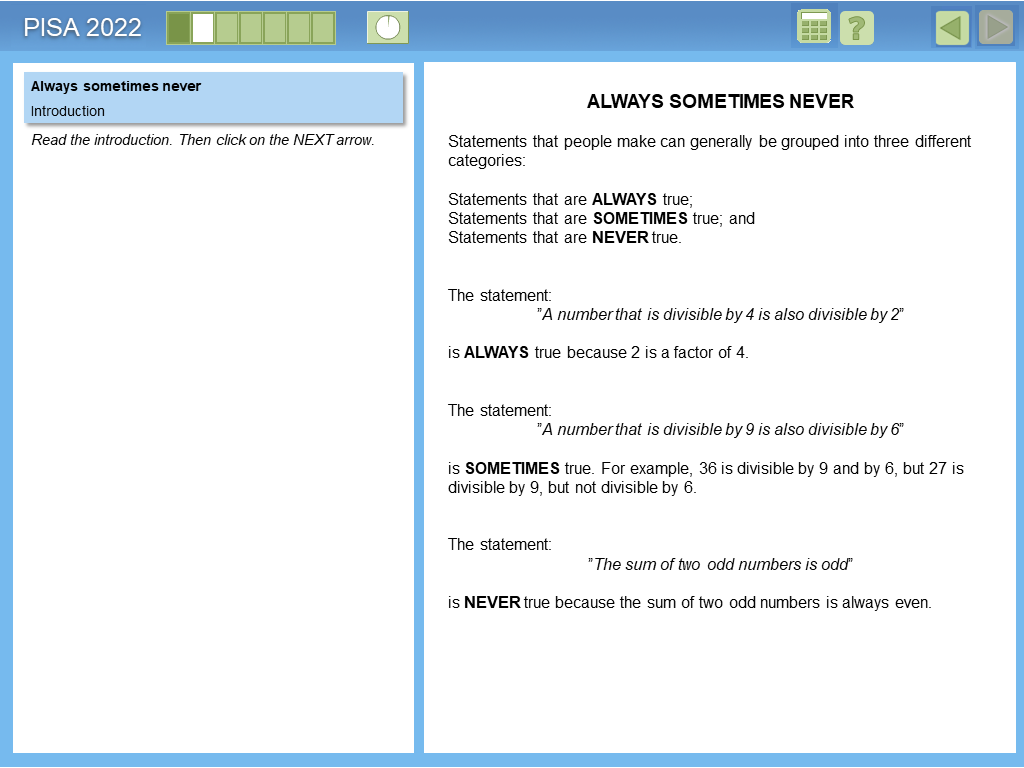
Example 3: Always Sometimes Never

This item illustrates a range of reasoning items from simple to more complex including a range of question types from yes/no and multiple choice to open-ended items.

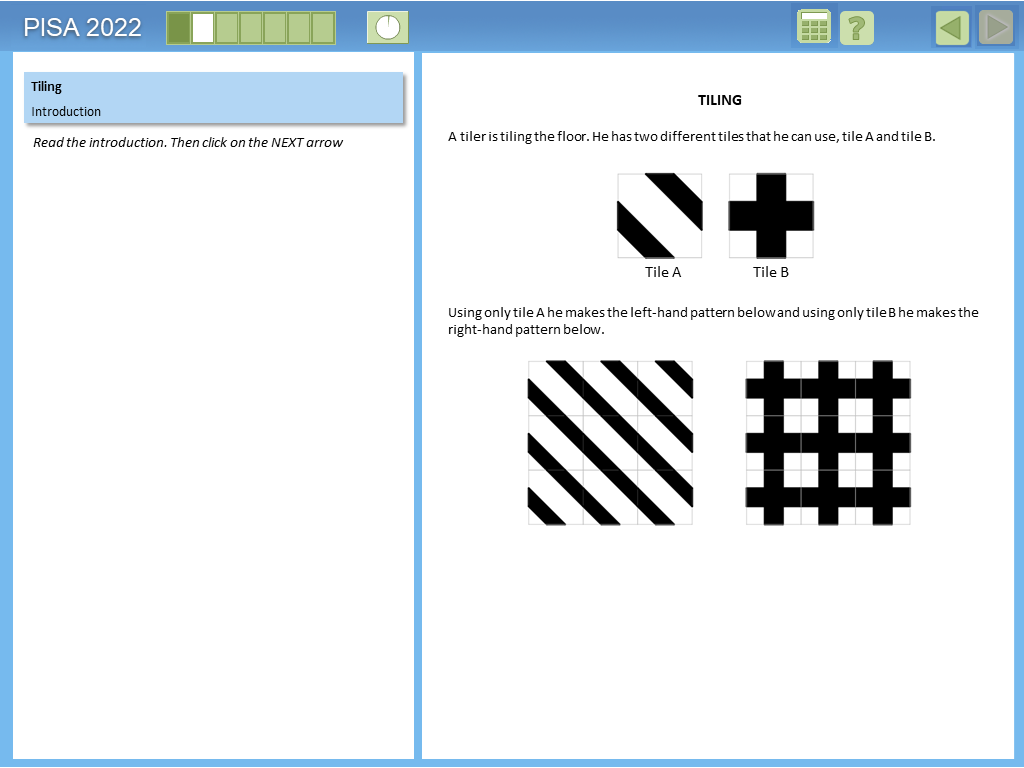
Example 4: Tiling

This item illustrates reasoning and computational thinking and geometric representations.

Example 5: Purchasing Decisions

This item illustrates the application of conditional decision making.

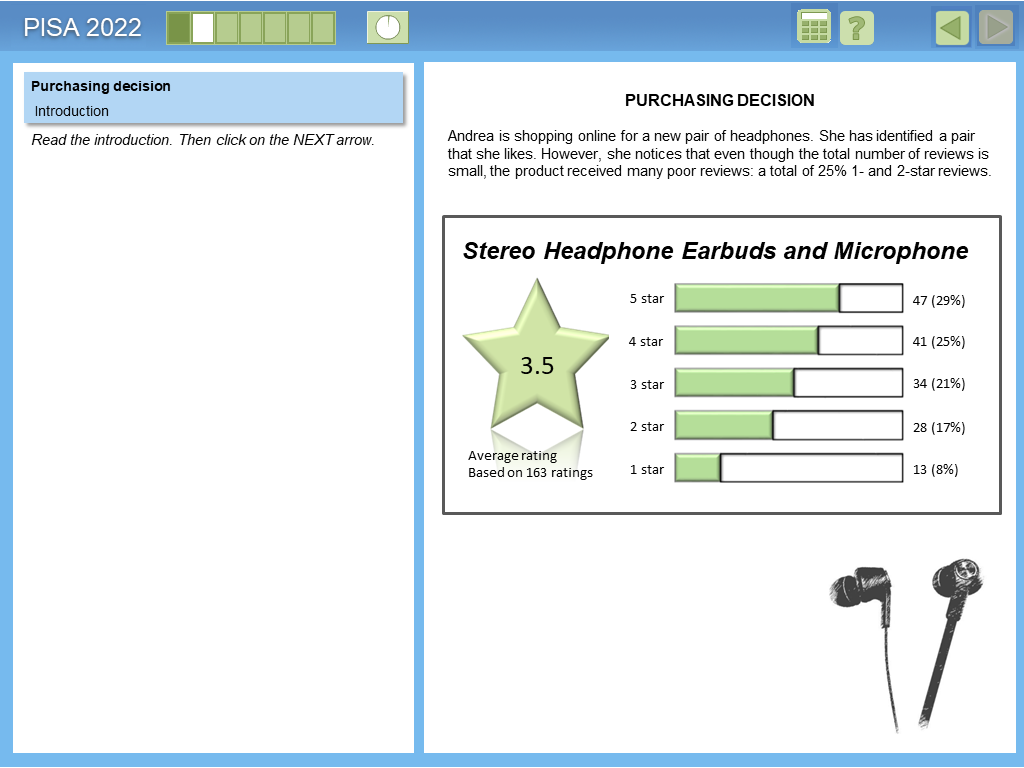
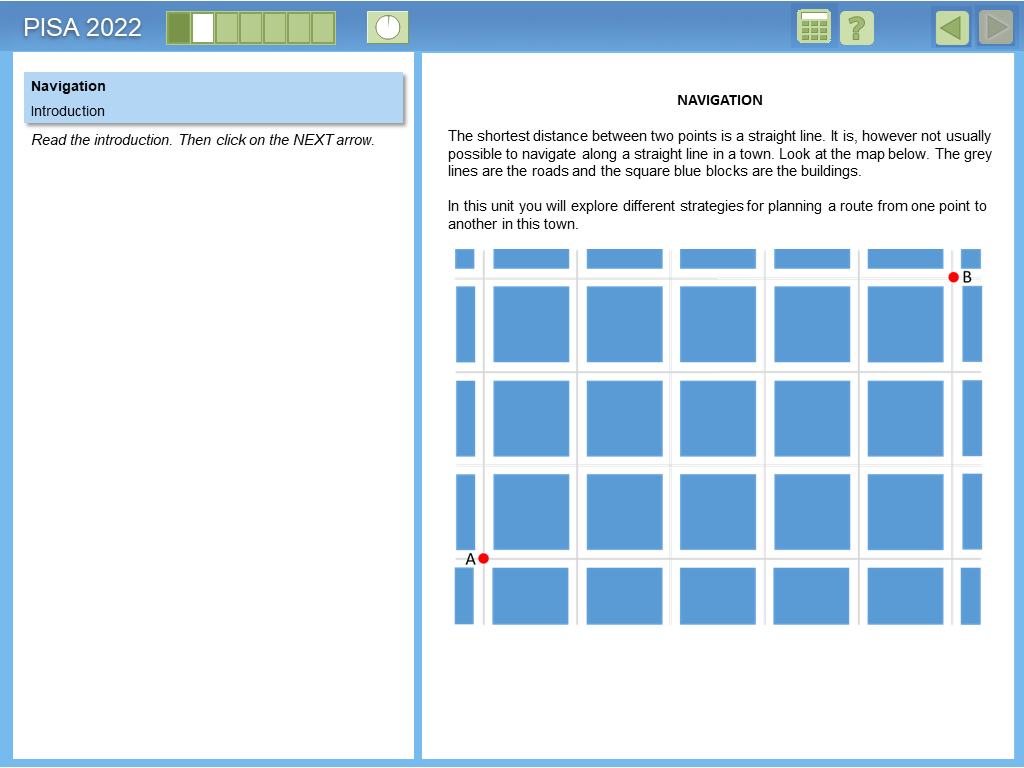
Example 6: Navigation

This item illustrates reasoning in a geometric context and computer-based assessment of mathematics (CBAM) capabilities in items.

Example 7: Savings Simulation

This item illustrates the use a computer simulation and hints at growth in the context and impact of interest.

Official launch of the Programme for International Student Assessment (PISA) 2022 Mathematics Framework

Date & time: october 14, 2019 15:00-16:30pm bst ( reception to follow ) location: somerville college, woodstock road, oxford, ox2 6hd, united kingdom.

Andreas Schleicher joins education experts from RTI International and Oxford University’s Centre for Educational Assessment in a panel discussion on October 14 from 15:00 to 16:30pm BST to launch the Programme for International Student Assessment (PISA) 2022 Mathematics Frameworks. The public event will be held at Somerville College in Oxford, UK and will be live streamed globally.

The mathematics framework was built by a team of global mathematics experts over the past 18 months and will define the theoretical underpinnings of the future PISA mathematics assessment. PISA is an international assessment conducted by the Organisation of Economic Co-operation and Development (OECD) that assess what 15-year-olds need to know and to be prepared for the future. The panel will discuss PISA in 2022, mathematics education in a global economy, and the importance of developing frameworks to guide assessments in the context of mathematics. Panel participants include:

• Andreas Schleicher , OECD, Director for Education and Skills
• Jason Hill , RTI International, Senior Research Analyst (moderator)
• Jenni Ingram , University of Oxford, Associate Professor of Mathematics Education
• Laurie Miles , SAS Software, Senior Director
• Lucy Dasgupta , John Mason School, Strategic Leader for Mathematics and Director of Teaching and Learning

Introduction and closure remarks by Therese N Hopfenbeck , Professor of Educational Assessment, Oxford University Centre for Educational Assessment.

Event Agenda

• 15:00-15:10 Welcome and introduction (Hopfenbeck)
• 15:10-15:20 PISA 2022 and the focus on mathematics (Schleicher)
• 15:20-15:30 Mathematics frameworks: the theoretical underpinnings of the PISA assessment (Ingram)
• 15:30-16:20 Panel discussion and questions from the audience
• 16:20-16:30 Closing Remarks (Hopfenbeck)
• 16:30 Reception

The Panelists

Therese N. Hopfenbeck

Jenni Ingram

Andreas Schleicher

Laurie Miles

Lucy Dasgupta

• Jason Hill , Senior Research Analyst, RTI International (moderator)
• Ezra Hodge , Amazon Web Services, AWS Training Education Programs Global Leader

Mathematical Competencies Framework Meets Problem-Solving Research in Mathematics Education

• First Online: 21 February 2023

Cite this chapter

• Mario Sánchez Aguilar   ORCID: orcid.org/0000-0002-1391-9388 20 ,
• Martha Leticia García Rodríguez   ORCID: orcid.org/0000-0003-2435-1334 20 &
• William Enrique Poveda Fernández   ORCID: orcid.org/0000-0002-7245-8278 21  

Part of the book series: Mathematics Education in the Digital Era ((MEDE,volume 20))

502 Accesses

In this chapter, it is argued that the mathematical competencies framework (Niss & Højgaard, 2011 ,  2019 ) is a suitable tool to study mathematical problem solving supported by the use of digital tools, and that its analytical power is strengthened by coordinating it with theoretical notions from research on mathematical problem solving. The chapter illustrates the potential of such networking of theories through the theoretical analysis of a mathematical problem-solving process of a preservice teacher supported by the use of a dynamic geometry system. This chapter not only exemplifies the potential of the networking of theories as a research practice, but also advances the mathematical competencies framework as another theoretical tool available to researchers interested in the study of mathematical problem solving.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

There are small differences between the names of the mathematical competencies as presented in Niss and Højgaard ( 2011 ) and Niss and Højgaard ( 2019 ). In this chapter, we use abbreviated versions of the competencies’ names as presented in Niss and Højgaard ( 2019 ).

Jacinto, H., & Carreira, S. (2017). Mathematical problem solving with technology: The techno-mathematical fluency of a student-with-GeoGebra. International Journal of Science and Mathematics Education, 15 (6), 1115–1136. https://doi.org/10.1007/s10763-016-9728-8

Article   Google Scholar  

Mousoulides, N., & Sriraman, B. (2020). Heuristics in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (2nd ed., pp. 331–333). Springer. https://doi.org/10.1007/978-3-030-15789-0_172

Niss, M., & Jensen, T. H. (2002). Kompetencer og matematiklæring—Ideer og inspiration til udvikling af matematikundervisning i Danmark [Competencies and mathematical learning—Ideas and inspiration for the development of mathematics teaching and learning in Denmark]. The Ministry of Education.

Google Scholar  

Niss, M., & Højgaard, T. (2011). Competencies and mathematical learning—ideas and inspiration for the development of mathematics teaching and learning in Denmark (No. 485). IMFUFA, Roskilde University. English translation of part I-VI of Niss and Jensen (2002).

Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102 (1), 9–28. https://doi.org/10.1007/s10649-019-09903-9

Polya. (1957). How to solve it: A new aspect of mathematical method (2nd ed.). Anchor Books (Original work published 1945).

Polya, G. (1981). Mathematical discovery: On understanding, learning, and teaching problem solving (Combined ed.). Wiley (Original work published 1962).

Prediger, S., & Bikner-Ahsbahs, A. (2014). Introduction to networking: Networking strategies and their background. In A. Bikner-Ahsbahs, & S. Prediger (Eds.), Networking of theories as a research practice in mathematics education (pp. 117–125). Springer. https://doi.org/10.1007/978-3-319-05389-9_8

Prediger, S., Bikner-Ahsbahs, A., & Arzarello, F. (2008). Networking strategies and methods for connecting theoretical approaches: First steps towards a conceptual framework. ZDM–The International Journal on Mathematics Education , 40 (2), 165–178. https://doi.org/10.1007/s11858-008-0086-z

Santos-Trigo, M. (2020). Problem-solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (2nd ed., pp. 686–693). Springer. https://doi.org/10.1007/978-3-030-15789-0_129

Santos-Trigo, M., & Camacho Machín, M. (2013). Framing the use of computational technology in problem solving approaches. The Mathematics Enthusiast, 10 (1–2), 279–302.

Schoenfeld, A. H. (1985). Mathematical problem solving . Academic Press.

Download references

Author information

Authors and affiliations.

Programa de Matemática Educativa, Instituto Politécnico Nacional, CICATA Legaria, Mexico city, Mexico

Mario Sánchez Aguilar & Martha Leticia García Rodríguez

Departamento de Educación Matemática, Escuela de Matemática, Universidad de Costa Rica, San José, Costa Rica

William Enrique Poveda Fernández

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Mario Sánchez Aguilar .

Editor information

Editors and affiliations.

Danish School of Education, Aarhus University, Copenhagen, Denmark

Uffe Thomas Jankvist

Curriculum, Pedagogy and Assessment, UCL Institute of Education, London, UK

Eirini Geraniou

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Aguilar, M.S., Rodríguez, M.L.G., Fernández, W.E.P. (2022). Mathematical Competencies Framework Meets Problem-Solving Research in Mathematics Education. In: Jankvist, U.T., Geraniou, E. (eds) Mathematical Competencies in the Digital Era. Mathematics Education in the Digital Era, vol 20. Springer, Cham. https://doi.org/10.1007/978-3-031-10141-0_5

Download citation

DOI : https://doi.org/10.1007/978-3-031-10141-0_5

Published : 21 February 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-10140-3

Online ISBN : 978-3-031-10141-0

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Intervention based on science of reading, math boosts comprehension, word problem-solving skills

English learners with math difficulty showed improvement following culturally-responsive training.

New research from the University of Kansas has found an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.

The intervention, performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students' performance when compared to students who received general instruction. That indicates emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.

"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems. This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems," said Michael Orosco, professor of educational psychology at KU and lead author of the study.

The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.

"It is proving to be one of the most effective evidence-based practices available for this growing population," Orosco said.

The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice .

For the research, trained tutors developed the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem that explained a person made a quesadilla for his friend Mario, giving him one-fourth of it, then needed to students to determine how much remained.

The tutor first asked students if they remembered a class session in which they made quesadillas, what shape they were and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator, and explaining that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.

"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."

Orosco, director of KU's Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario can impede subsequent problem-solving efforts.

The study proved effective in improving students' problem-solving abilities, despite covariates including an individual's basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key as, while ideally all students would begin on equal footing and there were little variations in a classroom, in reality, covariates exist and are commonplace.

The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.

The research builds on Orosco and colleagues' work in understanding and improving math instruction for English learners. Future work will continue to examine the role of cognitive functions such as working memory and brain science, as well as potential integration of artificial intelligence in teaching math.

"Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems," Orosco and Reed wrote. "Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition… Focusing on relevant language in word problems and providing collaborative support significantly improved students' solution accuracy."

• Learning Disorders
• K-12 Education
• Educational Psychology
• Intelligence
• Special education
• Problem solving
• Developmental psychology
• Child prodigy
• Intellectual giftedness
• Lateral thinking

Story Source:

Materials provided by University of Kansas . Original written by Mike Krings. Note: Content may be edited for style and length.

Journal Reference :

• Michael J. Orosco, Deborah K. Reed. Supplemental intervention for third-grade English learners with significant problem-solving challenges . Learning Disabilities Research & Practice , 2024; 39 (2): 60 DOI: 10.1177/09388982241229407

Cite This Page :

Explore More

• Anticoagulant With an On-Off Switch
• Sleep Resets Brain Connections -- At First
• Far-Reaching Effects of Exercise
• Hidden Connections Between Brain and Body
• Novel Genetic Plant Regeneration Approach
• Early Human Occupation of China
• Journey of Inhaled Plastic Particle Pollution
• Earth-Like Environment On Ancient Mars
• A 'Cosmic Glitch' in Gravity
• Time Zones Strongly Influence NBA Results

Trending Topics

Strange & offbeat.

Help | Advanced Search

Mathematics > Optimization and Control

Title: a modelling framework for energy-management and eco-driving problems using convex relaxations.

Abstract: This paper presents a convex optimization framework for eco-driving and vehicle energy management problems. We will first show that several types of eco-driving and vehicle energy management problems can be modelled using the same notions of energy storage buffers and energy storage converters that are connected to a power network. It will be shown that these problems can be formulated as optimization problems with linear cost functions and linear dynamics, and nonlinear constraints representing the power converters. We will show that under some mild conditions, the (non-convex) optimization problem has the same (globally) optimal solution as a convex relaxation. This means that the problems can be solved efficiently and that the solution is guaranteed to be globally optimal. Finally, a numerical example of the eco-driving problem is used to illustrate this claim.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .