hypothesis testing of standard deviation

Section 10.4: Hypothesis Tests for a Population Standard Deviation

• 10.1 The Language of Hypothesis Testing
• 10.2 Hypothesis Tests for a Population Proportion
• 10.3 Hypothesis Tests for a Population Mean
• 10.4 Hypothesis Tests for a Population Standard Deviation
• 10.5 Putting It Together: Which Method Do I Use?

By the end of this lesson, you will be able to...

• test hypotheses about a population standard deviation

For a quick overview of this section, watch this short video summary:

Before we begin this section, we need a quick refresher of the Χ 2 distribution.

The Chi-Square ( Χ 2 ) distribution

Reminder: "chi-square" is pronounced "kai" as in sky, not "chai" like the tea .

If a random sample size n is obtained from a normally distributed population with mean μ and standard deviation σ , then

has a chi-square distribution with n-1 degrees of freedom.

Properties of the Χ 2 distribution

• It is not symmetric.
• The shape depends on the degrees of freedom.
• As the number of degrees of freedom increases, the distribution becomes more symmetric.
• Χ 2 ≥0

Finding Probabilities Using StatCrunch

We again have some conditions that need to be true in order to perform the test 

• the sample was randomly selected, and
• the population from which the sample is drawn is normally distributed

Note that in the second requirement, the population must be normally distributed. The steps in performing the hypothesis test should be familiar by now.

Performing a Hypothesis Test Regarding σ

Step 1 : State the null and alternative hypotheses.

Step 2 : Decide on a level of significance, α .

Step 4 : Determine the P -value.

Step 5 : Reject the null hypothesis if the P -value is less than the level of significance, α.

Step 6 : State the conclusion.

In Example 2 , in Section 10.2, we assumed that the standard deviation for the resting heart rates of ECC students was 12 bpm. Later, in Example 2 in Section 10.3, we considered the actual sample data below.

( Click here to view the data in a format more easily copied.)

Based on this sample, is there enough evidence to say that the standard deviation of the resting heart rates for students in this class is different from 12 bpm?

Note: Be sure to check that the conditions for performing the hypothesis test are met.

[ reveal answer ]

From the earlier examples, we know that the resting heart rates could come from a normally distributed population and there are no outliers.

Step 1 : H 0 : σ = 12 H 1 : σ ≠ 12

Step 2 : α = 0.05

Step 4 : P -value = 2P( Χ 2 > 15.89) ≈ 0.2159

Step 5 : Since P -value > α , we do not reject H 0 .

Step 6 : There is not enough evidence at the 5% level of significance to support the claim that the standard deviation of the resting heart rates for students in this class is different from 12 bpm.

Hypothesis Testing Regarding σ Using StatCrunch

Let's look at Example 1 again, and try the hypothesis test with technology.

Using DDXL:

Using StatCrunch:

<< previous section | next section >>

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Prevent plagiarism. Run a free check.

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved April 10, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

6.5 Introduction to Hypothesis Tests

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter.

Another way to make a statistical inference is to make a decision about a parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.  A statistician may want to make a decision about or evaluate these claims. A hypothesis test can be used to do this .

A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.

In this section you will conduct hypothesis tests on single means when the population standard deviation is known.

Hypothesis testing consists of two contradictory hypotheses or statements, a decision based on the data, and a conclusion. To perform a hypothesis test, a statistician will perform some variation of these steps:

• Define hypotheses.
• Collect and/OR use the sample data to determine the correct distribution to use.
• Calculate Test Statistic.
• Make a decision
• Write a conclusion.

Defining your hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

The null hypothesis ( H 0 ): It is often a statement of the accepted historical value or norm. This is your starting point that you must assume from the beginning in order to show an effect exists.

The alternative hypothesis ( H a ) : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision . There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical symbols used in H 0 and H a :

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null hypothesis is: H 0 : μ = 2.0. What is the alternative hypothesis?

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

Using the Sample to Test the Null Hypothesis

Once you have defined your hypotheses the next step in the process, is to collect sample data.  In a classroom context most of the time the data or summary statistics will be given to you.

Then you will have to determine the correct distribution to perform the hypothesis test, given the assumptions you are able to make about the situation.  Right now we are demonstrating these ideas in a test for a mean when the population standard deviation is known using the Z distribution.  We will see other scenarios in the future.

Calculating a Test Statistic

Next, you will start evaluating the data.  This begins with calculating your test statistic , which is a measure of how far what you observed is from what you are assuming to he true.  In this context, your test statistic, z ο , quantifies the number of standard deviations between the sample mean x and the population mean µ.  Calculating the test statistic is analogous to standardizing observations with Z-scores as discussed previously:

where µ o   is the value assumed to be true in the null hypothesis.

Making a Decision

Once you have your test statistic there are two methods to use it to make your decision:

• Critical value method – This is one way you can make a decision, but will not be discussed in detail at this time.
• P-Value method – This is the preferred method we will focus on.

P-Value Method

To find a p-value we use the test statistic to calculate the actual probability of getting the test result. Formally, the p -value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample.

A large p -value calculated from the data indicates that we should not reject the null hypothesis. The smaller the p -value, the more unlikely the outcome, and the stronger the evidence is against the null hypothesis. We would reject the null hypothesis if the evidence is strongly against it.

Draw a graph that shows the p -value. The hypothesis test is easier to perform if you use a graph because you see the problem more clearly.

Suppose a baker claims that his bread height is more than 15 cm, on average. Several of his customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm. The baker knows from baking hundreds of loaves of bread that the standard deviation for the height is 0.5 cm. and the distribution of heights is normal.

The null hypothesis could be H 0 : μ ≤ 15

The alternate hypothesis is H a : μ > 15

The words “is more than” translates as a “>” so “ μ > 15″ goes into the alternate hypothesis. The null hypothesis must contradict the alternate hypothesis.

Suppose the null hypothesis is true (the mean height of the loaves is no more than 15 cm). Then is the mean height (17 cm) calculated from the sample unexpectedly large? The hypothesis test works by asking the question how unlikely the sample mean would be if the null hypothesis were true. The graph shows how far out the sample mean is on the normal curve. The p -value is the probability that, if we were to take other samples, any other sample mean would fall at least as far out as 17 cm.

The p -value, then, is the probability that a sample mean is the same or greater than 17 cm. when the population mean is, in fact, 15 cm. We can calculate this probability using the normal distribution for means.

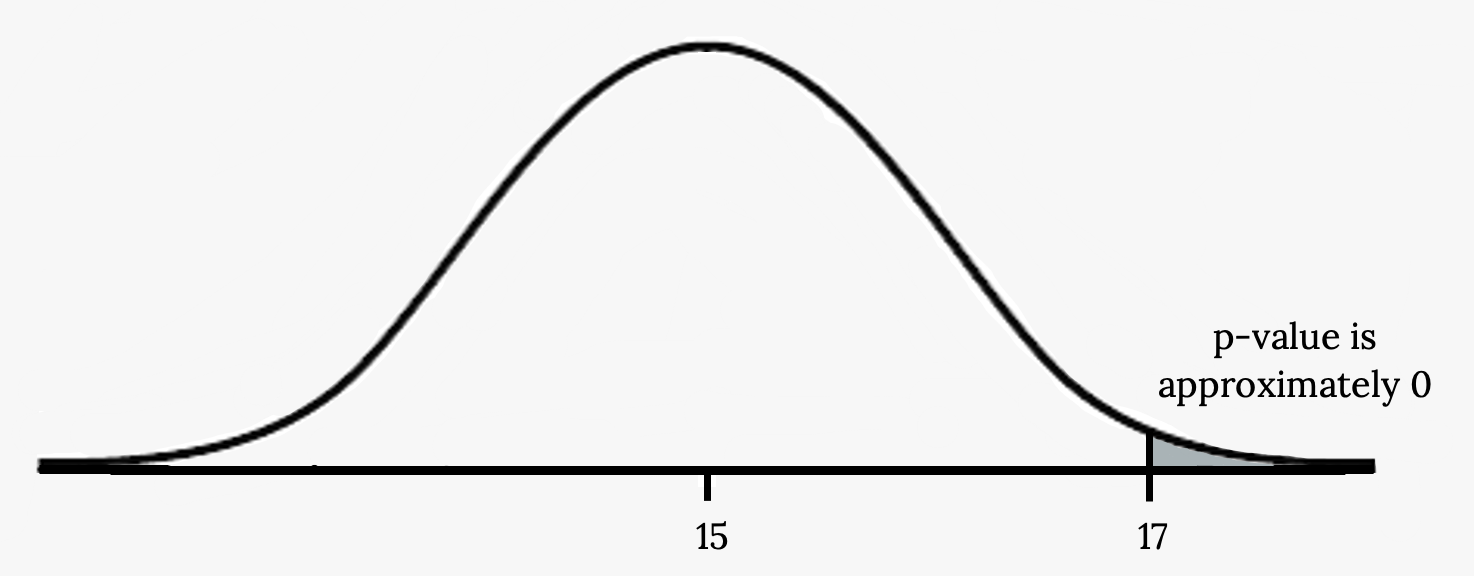
A p -value of approximately zero tells us that it is highly unlikely that a loaf of bread rises no more than 15 cm, on average. That is, almost 0% of all loaves of bread would be at least as high as 17 cm. purely by CHANCE had the population mean height really been 15 cm. Because the outcome of 17 cm. is so unlikely (meaning it is happening NOT by chance alone), we conclude that the evidence is strongly against the null hypothesis (the mean height is at most 15 cm.). There is sufficient evidence that the true mean height for the population of the baker’s loaves of bread is greater than 15 cm.

A normal distribution has a standard deviation of 1. We want to verify a claim that the mean is greater than 12. A sample of 36 is taken with a sample mean of 12.5.

Find The P-value:

Decision and conclusion

A systematic way to make a decision of whether to reject or not reject the null hypothesis is to compare the p -value and a preset or preconceived α (also called a significance level ). A preset α is the probability of a Type I error (rejecting the null hypothesis when the null hypothesis is true). It may or may not be given to you at the beginning of the problem.  If there is no given preconceived α , then use α = 0.05.

When you make a decision to reject or not reject H 0 , do as follows:

• If α > p -value, reject H 0 . The results of the sample data are statistically significant . You can say there is sufficient evidence to conclude that H 0 is an incorrect belief and that the alternative hypothesis, H a , may be correct.
• If α ≤ p -value, fail to reject H 0 . The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis, H a , may be correct.

After you make your decision, write a thoughtful conclusion in the context of the scenario incorporating the hypotheses.

NOTE: When you “do not reject H 0 “, it does not mean that you should believe that H 0 is true. It simply means that the sample data have failed to provide sufficient evidence to cast serious doubt about the truthfulness of H o .

When using the p -value to evaluate a hypothesis test, it is sometimes useful to use the following memory device

If the p -value is low, the null must go.

If the p -value is high, the null must fly.

This memory aid relates a p -value less than the established alpha (the p is low) as rejecting the null hypothesis and, likewise, relates a p -value higher than the established alpha (the p is high) as not rejecting the null hypothesis.

Fill in the blanks.

Reject the null hypothesis when                            .

The results of the sample data                           .

Do not reject the null when hypothesis when                           .

It’s a Boy Genetics Labs claim their procedures improve the chances of a boy being born. The results for a test of a single population proportion are as follows:

H 0 : p = 0.50, H a : p > 0.50

p -value = 0.025

Interpret the results and state a conclusion in simple, non-technical terms.

Image Credits

Figure 6.11: Alora Griffiths (2019). “Dalmation puppy near man…” Public domain. Retrieved from https://unsplash.com/photos/7aRQZtLsvqw

Figure 6.13: Kindred Grey via Virginia Tech (2020). “Figure 6.11” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_6.11.png . Adaptation of Figure 5.39 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/5-practice

A decision making procedure for determining whether sample evidence supports a hypothesis

The claim that is assumed to be true and is tested in a hypothesis test

A working hypothesis that is contradictory to the null hypothesis

A measure of how far what you observed is from the hypothesized (or claimed) value

The probability that an event will occur, assuming the null hypothesis is true

Probability that a true null hypothesis will be rejected, also known as Type I error and denoted by α

Finding sufficient evidence that the effect we see is not just due to variability, often from rejecting the null hypothesis

Significant Statistics Copyright © 2020 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Hypothesis Test for Population Standard Deviation for normal population

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.7 Hypothesis Tests for a Population Mean with Unknown Population Standard Deviation

Learning objectives.

• Conduct and interpret hypothesis tests for a population mean with unknown population standard deviation.

Some notes about conducting a hypothesis test:

• The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
• The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
• If the alternative hypothesis is a “less than”,  then the test is left-tail.  The p -value is the area in the left-tail of the distribution.
• If the alternative hypothesis is a “greater than”, then the test is right-tail.  The p -value is the area in the right-tail of the distribution.
• If the alternative hypothesis is a “not equal to”, then the test is two-tail.  The p -value is the sum of the area in the two-tails of the distribution.  Each tail represents exactly half of the p -value.
• Think about the meaning of the p -value.  A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of  0.05.  Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis.  This makes the data analyst use judgment rather than mindlessly applying rules.
• The significance level must be identified before collecting the sample data and conducting the test.  Generally, the significance level will be included in the question.  If no significance level is given, a common standard is to use a significance level of 5%.
• An alternative approach for hypothesis testing is to use what is called the critical value approach .  In this book, we will only use the p -value approach.  Some of the videos below may mention the critical value approach, but this approach will not be used in this book.

Steps to Conduct a Hypothesis Test for a Population Mean with Unknown Population Standard Deviation

• Write down the null and alternative hypotheses in terms of the population mean [latex]\mu[/latex].  Include appropriate units with the values of the mean.
• Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
• Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ \\ df & = & n-1 \\ \\ \end{eqnarray*}[/latex]

• The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION MEAN WITH UNKNOWN POPULATION STANDARD DEVIATION

The p -value for a hypothesis test on a population mean is the area in the tail(s) of the distribution of the sample mean.  When the population standard deviation is unknown, use the [latex]t[/latex]-distribution to find the p -value.

If the p -value is the area in the left-tail:

• For t-score , enter the value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex].
• For degrees of freedom , enter the degrees of freedom for the [latex]t[/latex]-distribution [latex]n-1[/latex].
• For the logic operator , enter true .  Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.
• The output from the t.dist function is the area under the [latex]t[/latex]-distribution to the left of the entered [latex]t[/latex]-score.
• Visit the Microsoft page for more information about the t.dist function.

If the p -value is the area in the right-tail:

• The output from the t.dist.rt function is the area under the [latex]t[/latex]-distribution to the right of the entered [latex]t[/latex]-score.
• Visit the Microsoft page for more information about the t.dist.rt function.

If the p -value is the sum of area in the tails:

• For t-score , enter the absolute value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex].  Note:  In the t.dist.2t function, the value of the [latex]t[/latex]-score must be a positive number.  If the [latex]t[/latex]-score is negative, enter the absolute value of the [latex]t[/latex]-score into the t.dist.2t function.
• The output from the t.dist.2t function is the sum of areas in the tails under the [latex]t[/latex]-distribution.
• Visit the Microsoft page for more information about the t.dist.2t function.

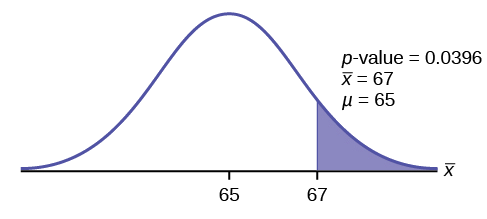
Statistics students believe that the mean score on the first statistics test is 65.  A statistics instructor thinks the mean score is higher than 65.  He samples ten statistics students and obtains the following scores:

The instructor performs a hypothesis test using a 1% level of significance. The test scores are assumed to be from a normal distribution.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \mu=65  \\ H_a: & & \mu \gt 65  \end{eqnarray*}[/latex]

From the question, we have [latex]n=10[/latex], [latex]\overline{x}=67[/latex], [latex]s=3.1972...[/latex] and [latex]\alpha=0.01[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=3.1972...[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right-tail of the distribution.

To use the t.dist.rt function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{67-65}{\frac{3.1972...}{\sqrt{10}}} \\ & = & 1.9781... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=10-1=9[/latex].

So the p -value[latex]=0.0396[/latex].

Conclusion:

Because p -value[latex]=0.0396 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that mean score on the test is greater than 65.

• The null hypothesis [latex]\mu=65[/latex] is the claim that the mean test score is 65.
• The alternative hypothesis [latex]\mu \gt 65[/latex] is the claim that the mean test score is greater than 65.
• Keep all of the decimals throughout the calculation (i.e. in the sample standard deviation, the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p -value.  This ensures that we get the most accurate value for the p -value.
• The p -value is the area in the right-tail of the [latex]t[/latex]-distribution, to the right of [latex]t=1.9781...[/latex].
• The p -value of 0.0396 tells us that under the assumption that the mean test score is 65 (the null hypothesis), there is a 3.96% chance that the mean test score is 65 or more.  Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.

A company claims that the average change in the value of their stock is $3.50 per week.  An investor believes this average is too high. The investor records the changes in the company’s stock price over 30 weeks and finds the average change in the stock price is $2.60 with a standard deviation of $1.80.  At the 5% significance level, is the average change in the company’s stock price lower than the company claims?

[latex]\begin{eqnarray*} H_0: & & \mu=$3.50  \\ H_a: & & \mu \lt $3.50  \end{eqnarray*}[/latex]

From the question, we have [latex]n=30[/latex], [latex]\overline{x}=2.6[/latex], [latex]s=1.8[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=1.8.[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left-tail of the distribution.

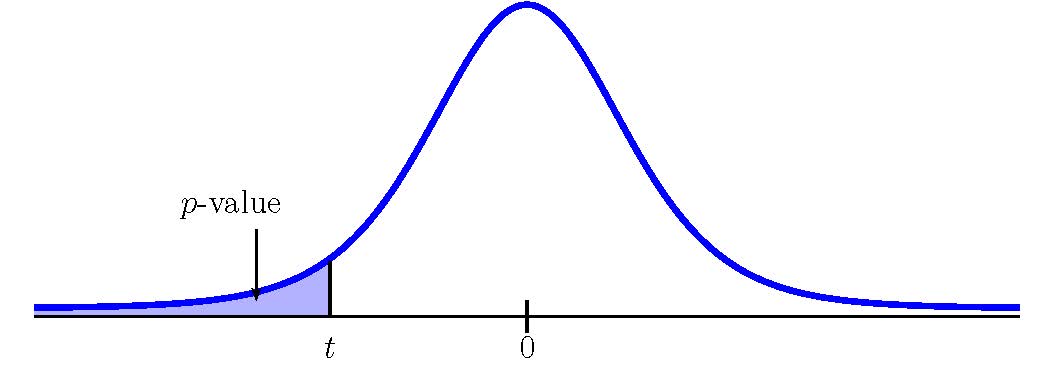
To use the t.dist function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{2.6-3.5}{\frac{1.8}{\sqrt{30}}} \\ & = & -1.5699... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=30-1=29[/latex].

So the p -value[latex]=0.0636[/latex].

Because p -value[latex]=0.0636 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that average change in the stock price is lower than $3.50.

• The null hypothesis [latex]\mu=$3.50[/latex] is the claim that the average change in the company’s stock is $3.50 per week.
• The alternative hypothesis [latex]\mu \lt $3.50[/latex] is the claim that the average change in the company’s stock is less than $3.50 per week.
• The p -value is the area in the left-tail of the [latex]t[/latex]-distribution, to the left of [latex]t=-1.5699...[/latex].
• The p -value of 0.0636 tells us that under the assumption that the average change in the stock is $3.50 (the null hypothesis), there is a 6.36% chance that the average change is $3.50 or less.  Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the company’s claim that the average change in their stock price is $3.50 per week is most likely correct.

A paint manufacturer has their production line set-up so that the average volume of paint in a can is 3.78 liters.  The quality control manager at the plant believes that something has happened with the production and the average volume of paint in the cans has changed.  The quality control department takes a sample of 100 cans and finds the average volume is 3.62 liters with a standard deviation of 0.7 liters.  At the 5% significance level, has the volume of paint in a can changed?

[latex]\begin{eqnarray*} H_0: & & \mu=3.78 \mbox{ liters}  \\ H_a: & & \mu \neq 3.78 \mbox{ liters}  \end{eqnarray*}[/latex]

From the question, we have [latex]n=100[/latex], [latex]\overline{x}=3.62[/latex], [latex]s=0.7[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=0.7[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

To use the t.dist.2t function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{3.62-3.78}{\frac{0.07}{\sqrt{100}}} \\ & = & -2.2857... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=100-1=99[/latex].

So the p -value[latex]=0.0244[/latex].

Because p -value[latex]=0.0244 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that average volume of paint in the cans has changed.

• The null hypothesis [latex]\mu=3.78[/latex] is the claim that the average volume of paint in the cans is 3.78.
• The alternative hypothesis [latex]\mu \neq 3.78[/latex] is the claim that the average volume of paint in the cans is not 3.78.
• Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score) to avoid any round-off error in the calculation of the p -value.  This ensures that we get the most accurate value for the p -value.
• The p -value is the sum of the area in the two tails.  The output from the t.dist.2t function is exactly the sum of the area in the two tails, and so is the p -value required for the test.  No additional calculations are required.
• The t.dist.2t function requires that the value entered for the [latex]t[/latex]-score is positive .  A negative [latex]t[/latex]-score entered into the t.dist.2t function generates an error in Excel.  In this case, the value of the [latex]t[/latex]-score is negative, so we must enter the absolute value of this [latex]t[/latex]-score into field 1.
• The p -value of 0.0244 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the average volume of paint in the cans has most likely changed from 3.78 liters.

Watch this video: Hypothesis Testing: t -test, right tail by ExcelIsFun [11:02]

Watch this video: Hypothesis Testing: t -test, left tail by ExcelIsFun [7:48]

Watch this video: Hypothesis Testing: t -test, two tail by ExcelIsFun [8:54]

Concept Review

The hypothesis test for a population mean is a well established process:

• Collect the sample information for the test and identify the significance level.
• When the population standard deviation is unknown, find the p -value (the area in the corresponding tail) for the test using the [latex]t[/latex]-distribution with [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex] and [latex]df=n-1[/latex].
• Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 9.6   Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License.

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: Hypothesis Test Examples for Means with Unknown Standard Deviation

• Last updated
• Save as PDF
• Page ID 11532

Full Hypothesis Test Examples

Example \(\PageIndex{6}\)

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that \(\alpha = 0.05\). This is a test of a single population mean .

\(H_{0}: \mu = 65  H_{a}: \mu > 65\)

Since the instructor thinks the average score is higher, use a "\(>\)". The "\(>\)" means the test is right-tailed.

Determine the distribution needed:

Random variable: \(\bar{X} =\) average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given \(n = 10\) sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's \(t\).

Use \(t_{df}\). Therefore, the distribution for the test is \(t_{9}\) where \(n = 10\) and \(df = 10 - 1 = 9\).

Calculate the \(p\)-value using the Student's \(t\)-distribution:

\(p\text{-value} = P(\bar{x} > 67) = 0.0396\) where the sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

Compare \(\alpha\) and the \(p-\text{value})\:

Since \( α = 0.05\) and \(p\text{-value} = 0.0396\). \(\alpha > p\text{-value}\).

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\).

This means you reject \(\mu = 65\). In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The \(p\text{-value}\) can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq: . Arrow down to \(\mu\): and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p\text{-value}\) (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 65\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \( t = 1.9781\) (test statistic) and \(p = 0.0396\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Exercise \(\PageIndex{6}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: \mu = 5\)
• \(H_{a}: \mu < 5\)
• \(p = 0.0082\)

Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

• Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example \(\PageIndex{10}\)

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations : We will input the sample data into the TI-83 as follows.

4. State the Conclusions : Since the \(p\text{-value} (p = 0.036)\) is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at http://www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12, hypothesis testing and p-values.

• One-tailed and two-tailed tests
• Z-statistics vs. T-statistics
• Small sample hypothesis test
• Large sample proportion hypothesis testing

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Hypothesis Testing for the Standard Deviation
• Why is important to perform a hypothesis test about a standard deviation?
• What are the two conditions that must be met when performing a hypothesis test about the standard deviation?
• What test can be used to determine if two samples have similar variances?
• What causes the null hypothesis to be rejected in an F-test?

Advanced Topics

• Nonlinear Transformations of Data
• Nonparametric Statistics
• Analysis of Variance

Hypothesis Testing for Means & Proportions

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.  

This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests. 

Learning Objectives

After completing this module, the student will be able to:

• Define null and research hypothesis, test statistic, level of significance and decision rule
• Distinguish between Type I and Type II errors and discuss the implications of each
• Explain the difference between one and two sided tests of hypothesis
• Estimate and interpret p-values
• Explain the relationship between confidence interval estimates and p-values in drawing inferences
• Differentiate hypothesis testing procedures based on type of outcome variable and number of sample

Introduction to Hypothesis Testing

Techniques for hypothesis testing  .

The techniques for hypothesis testing depend on

• the type of outcome variable being analyzed (continuous, dichotomous, discrete)
• the number of comparison groups in the investigation
• whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).

In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).

General Approach: A Simple Example

The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002.   In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.  

In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:

Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,

(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.

Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:

How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,

There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?  

Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.

In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.

First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.  

In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.

α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).

Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.  

Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.  

With the first sample we have

Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

Tests with One Sample, Continuous Outcome

Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ 0 ). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.

Test Statistics for Testing H 0 : μ= μ 0

• if n > 30
• if n < 30

Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value. 

The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races.  The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured.   The sample data are summarized as follows: n=100, x̄

=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach. 

• Step 1.  Set up hypotheses and determine level of significance

H 0 : μ = 3,302 H 1 : μ < 3,302           α =0.05

The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.

This is a lower tailed test, using a Z statistic and a 5% level of significance.   Reject H 0 if Z < -1.645.

•   Step 4. Compute the test statistic.  

We do not reject H 0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.  

Recall that when we fail to reject H 0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H 0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H 0 . We do not conclude that H 0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.      

The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?

Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.

H 0 : μ= 203 H 1 : μ≠ 203                       α=0.05

The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.

•   Step 3. Set up decision rule.  

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or is Z > 1.960.

We reject H 0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002.   Because we reject H 0 , we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.  

Statistical Significance versus Clinical (Practical) Significance

This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?  

Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol.   Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows:   n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach. 

H 0 : μ= 203 H 1 : μ< 203                   α=0.05

•  Step 2. Select the appropriate test statistic.  

Because the sample size is small (n<30) the appropriate test statistic is

This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows:   Reject H 0 if t < -2.145.

We do not reject H 0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H 0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.

Video - Comparing a Sample Mean to Known Population Mean (8:20)

Link to transcript of the video

Tests with One Sample, Dichotomous Outcome

Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p 0 ). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.    

In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,

We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.

Test Statistic for Testing H 0 : p = p 0

if min(np 0 , n(1-p 0 )) > 5

The formula above is appropriate for large samples, defined when the smaller of np 0 and n(1-p 0 ) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,

Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.

Example:  

The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%.  Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?

H 0 : p = 0.211 H 1 : p < 0.211                     α=0.05

We must first check that the sample size is adequate.   Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:

This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.645.

We reject H 0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.  

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

Calculate this on your own before checking the answer.

Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)

Tests with Two Independent Samples, Continuous Outcome

There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.

Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:

for sample 1:

for sample 2:

The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.  

In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ 1 -μ 2 . The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

The null hypothesis can also be written as follows: H 0 : μ 1 = μ 2 . In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H 1 : μ 1 > μ 2 ), that the first mean is smaller than the second (H 1 : μ 1 < μ 2 ), or that the means are different (H 1 : μ 1 ≠ μ 2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.

Test Statistics for Testing H 0 : μ 1 = μ 2

• if n 1 > 30 and n 2 > 30
• if n 1 < 30 or n 2 < 30

NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s 1 2 = s 2 2 ). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s 1 2 /s 2 2 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.    

The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s 1 and s 2 .)

Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.  

Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.  

H 0 : μ 1 = μ 2

H 1 : μ 1 ≠ μ 2                       α=0.05

Because both samples are large ( > 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s 1 2 /s 2 2 . Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.5 2 /20.1 2 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample.   Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.  

Now the test statistic:

We reject H 0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.  

Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.  

Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).  

A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.

Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.

H 0 : μ 1 = μ 2 H 1 : μ 1 < μ 2                         α=0.05

Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s 1 2 /s 2 2 =28.7 2 /30.3 2 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n 1 +n 2 -2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H 0 if t < -1.701.

Now the test statistic,

We reject H 0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.

The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.

Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)

Tests with Matched Samples, Continuous Outcome

In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μ d . The null hypothesis again reflects "no difference" and is stated as H 0 : μ d =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μ d =5) but in most instances the null hypothesis reflects no difference (i.e., μ d =0).  

The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.

Test Statistics for Testing H 0 : μ d =0

A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)

Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have

The calculations are shown below.  

Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.

H 0 : μ d = 0 H 1 : μ d > 0                 α=0.05

NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H 1 : μ d < 0. 

• Step 2 . Select the appropriate test statistic.

This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H 0 if t > 2.145.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.  

Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.

Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)

Tests with Two Independent Samples, Dichotomous Outcome

There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.

In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.      

For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2 .  

The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:

• For the risk difference, H 0 : p 1 - p 2 = 0 versus H 1 : p 1 - p 2 ≠ 0 which are, by definition, equal to H 0 : RD = 0 versus H 1 : RD ≠ 0.
• If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H 0 : RR = 1 versus H 1 : RR ≠ 1.
• If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H 0 : OR = 1 versus H 1 : OR ≠ 1.  

Suppose a test is performed to test H 0 : RD = 0 versus H 1 : RD ≠ 0 and the test rejects H 0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p 1 -p 2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H 0 : RD = 0. This is equivalent to H 0 : RR = 1 and H 0 : OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H 1 : p 1 > p 2 , which is equivalent to H 1 : RD > 0, H 1 : RR > 1 and H 1 : OR > 1), that the first proportion is smaller than the second (H 1 : p 1 < p 2 , which is equivalent to H 1 : RD < 0, H 1 : RR < 1 and H 1 : OR < 1), or that the proportions are different (H 1 : p 1 ≠ p 2 , which is equivalent to H 1 : RD ≠ 0, H 1 : RR ≠ 1 and H 1 : OR ≠

1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.  

The formula for the test of hypothesis for the difference in proportions is given below.

Test Statistics for Testing H 0 : p 1 = p

The formula above is appropriate for large samples, defined as at least 5 successes (np > 5) and at least 5 failures (n(1-p > 5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.

The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.

The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2                 α=0.05

• Step 2.  Select the appropriate test statistic.  

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5. Conclusion.

We do not reject H 0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.  

A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.    

Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.  

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2              α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

We reject H 0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.

A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result. 

Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).  

Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)

Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.

• Continuous Outcome, One Sample: H0: μ = μ0
• Continuous Outcome, Two Independent Samples: H0: μ1 = μ2
• Continuous Outcome, Two Matched Samples: H0: μd = 0
• Dichotomous Outcome, One Sample: H0: p = p 0
• Dichotomous Outcome, Two Independent Samples: H0: p1 = p2, RD=0, RR=1, OR=1

Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.

In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.    

We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.

Answers to Selected Problems

Dental services problem - bottom of page 5.

• Step 1: Set up hypotheses and determine the level of significance.

α=0.05

• Step 2: Select the appropriate test statistic.

First, determine whether the sample size is adequate.

Therefore the sample size is adequate, and we can use the following formula:

• Step 3: Set up the decision rule.

Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.

• Step 4: Compute the test statistic
• Step 5: Conclusion.

We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.6: Hypothesis Test of a Single Population Mean with Examples

• Last updated
• Save as PDF
• Page ID 130297

Steps for performing Hypothesis Test of a Single Population Mean

Step 1: State your hypotheses about the population mean. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure

• Find or identify the sample size, n, the sample mean, \(\bar{x}\) and the sample standard deviation, s .

The sampling distribution for the one-mean test statistic is, approximately, T- distribution if the following conditions are met

• Sample is random with independent observations .
• Sample is large. The population must be Normal or the sample size must be at least 30.

Step 3: Perform the procedure based on the assumption that \(H_{0}\) is true

• Find the Estimated Standard Error: \(SE=\frac{s}{\sqrt{n}}\).
• Compute the observed value of the test statistic: \(T_{obs}=\frac{\bar{x}-\mu_{0}}{SE}\).
• Check the type of the test (right-, left-, or two-tailed)
• Find the p-value in order to measure your level of surprise.

Step 4: Make a decision about \(H_{0}\) and \(H_{a}\)

• Do you reject or not reject your null hypothesis?

Step 5: Make a conclusion

• What does this mean in the context of the data?

The following examples illustrate a left-, right-, and two-tailed test.

Example \(\pageindex{1}\).

\(H_{0}: \mu = 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

Exercise \(\PageIndex{1}\)

\(H_{0}: \mu = 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

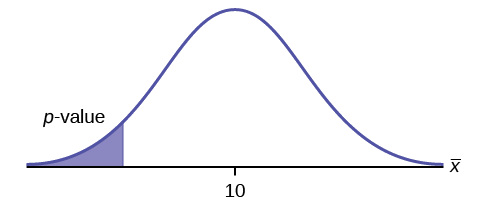
Example \(\PageIndex{2}\)

\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

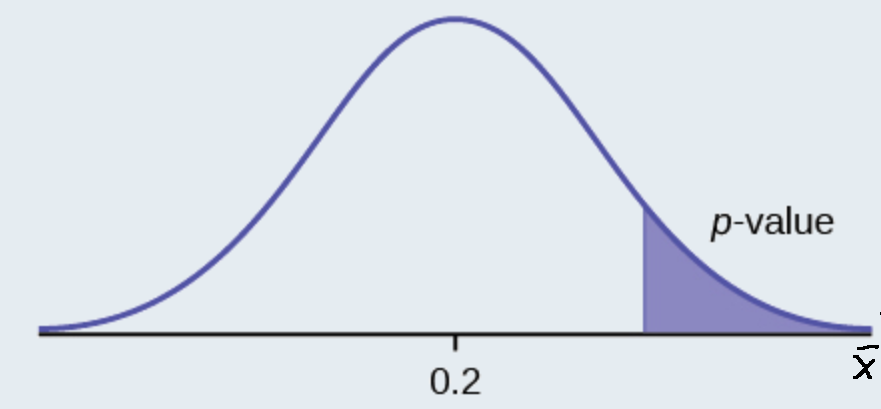
Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

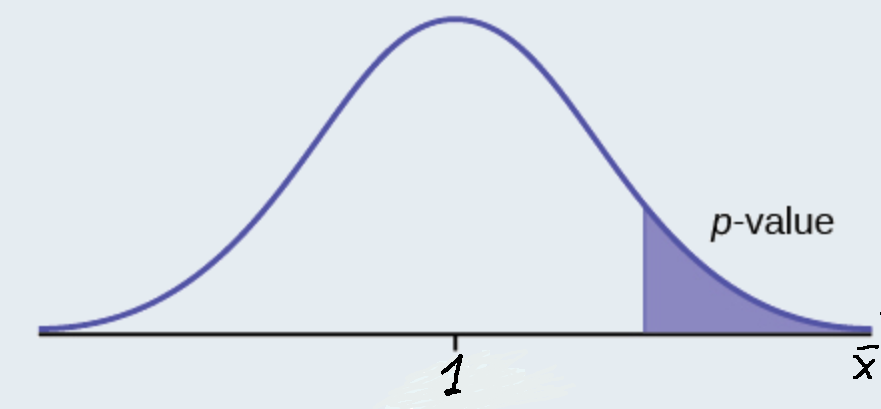
Example \(\PageIndex{3}\)

\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

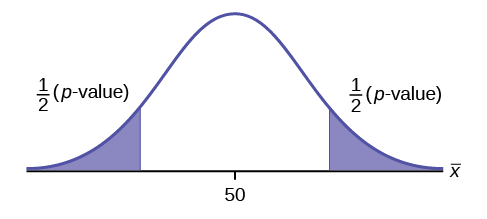
Exercise \(\PageIndex{3}\)

\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

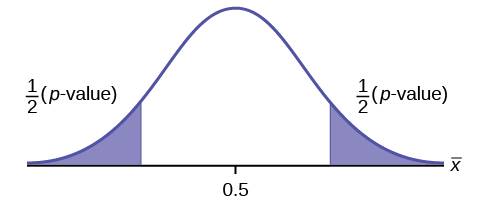
Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that \(\alpha = 0.05\). This is a test of a single population mean .

\(H_{0}: \mu = 65  H_{a}: \mu > 65\)

Since the instructor thinks the average score is higher, use a "\(>\)". The "\(>\)" means the test is right-tailed.

Determine the distribution needed:

Random variable: \(\bar{X} =\) average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given \(n = 10\) sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's \(t\).

Use \(t_{df}\). Therefore, the distribution for the test is \(t_{9}\) where \(n = 10\) and \(df = 10 - 1 = 9\).

The sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Calculate the \(p\)-value using the Student's \(t\)-distribution:

\[t_{obs} = \dfrac{\bar{x}-\mu_{\bar{x}}}{\left(\dfrac{s}{\sqrt{n}}\right)}=\dfrac{67-65}{\left(\dfrac{3.1972}{\sqrt{10}}\right)}\]

Use the T-table or Excel's t_dist() function to find p-value:

\(p\text{-value} = P(\bar{x} > 67) =P(T >1.9782 )= 1-0.9604=0.0396\)

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

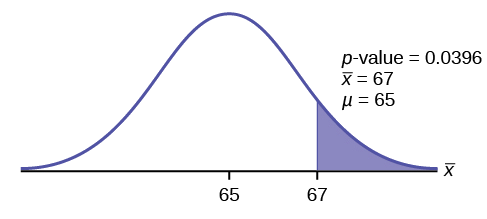
Compare \(\alpha\) and the \(p-\text{value}\):

Since \(α = 0.05\) and \(p\text{-value} = 0.0396\). \(\alpha > p\text{-value}\).

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\).

This means you reject \(\mu = 65\). In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The \(p\text{-value}\) can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq: . Arrow down to \(\mu\): and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p\text{-value}\) (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 65\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(t = 1.9781\) (test statistic) and \(p = 0.0396\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Exercise \(\PageIndex{4}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: \mu = 5\)
• \(H_{a}: \mu < 5\)
• \(p = 0.0082\)

Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

• Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example \(\PageIndex{5}\)

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations : \(p\text{-value} ( = 0.036)\)

4. State the Conclusions : Since the \(p\text{-value} (= 0.036)\) is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A t -score is an example of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).