problem solving in maths research

Featured Topics

Featured series.

A series of random questions answered by Harvard experts.

Explore the Gazette

Read the latest.

Harvard stargazer whose humanity still burns bright

Taiwan sees warning signs in weakening congressional support for Ukraine

How dating sites automate racism

“Teachers should teach math in a way that encourages students to engage in sense-making and not merely to memorize or internalize exactly what the teacher says or does,” says Jon R. Star.

Kris Snibbe/Harvard Staff Photographer

One way is the wrong way to do math. Here’s the right way.

Harvard Staff Writer

Research by Ed School psychologist reinforces case for stressing multiple problem-solving paths over memorization

There’s never just one way to solve a math problem, says Jon R. Star , a psychologist and professor of education at the Harvard Graduate School of Education. With researchers from Vanderbilt University, Star found that teaching students multiple ways to solve math problems instead of using a single method improves teaching and learning. In an interview with the Gazette, Star, a former math teacher, outlined the research and explained how anyone, with the right instruction, can develop a knack for numbers.

Jon R. Star

GAZETTE: What is the most common misconception about math learning?

STAR: That you’re either a math person or you’re not a math person — that some people are just born with math smarts, and they can do math, and other people are just not, and there’s not much you can do about it.

GAZETTE: What does science say about the process of learning math?

STAR: One thing we know from psychology about the learning process is that the act of reaching into your brain, grabbing some knowledge, pulling it out, chewing on it, talking about it, and putting it back helps you learn. Psychologists call this elaborative encoding. The more times you can do that process — putting knowledge in, getting it out, elaborating on it, putting it back in — the more you will have learned, remembered, and understood the material. We’re trying to get math teachers to help students engage in that process of elaborative encoding.

GAZETTE: How did you learn math yourself?

STAR: Learning math should involve some sense-making. It’s necessary that we listen to what our teacher tells us about the math and try to make sense of it in our minds. Math learning is not about pouring the words directly from the teacher’s mouth into the students’ ears and brains. That’s not the way it works. I think that’s how I learned math. But that’s not how I hope students learn math and that’s not how I hope teachers think about the teaching of math. Teachers should teach math in a way that encourages students to engage in sense-making and not merely to memorize or internalize exactly what the teacher says or does.

GAZETTE: Tell us about the teaching method described in the research.

STAR: One of the strategies that some teachers may use when teaching math is to show students how to solve problems and expect that the student is going to end up using the same method that the teacher showed. But there are many ways to solve math problems; there’s never just one way.

The strategy we developed asks that teachers compare two ways for solving a problem, side by side, and that they follow an instructional routine to lead a discussion to help students understand the difference between the two methods. That discussion is really the heart of this routine because it is fundamentally about sharing reasoning: Teachers ask students to explain why a strategy works, and students must dig into their heads and try to say what they understand. And listening to other people’s reasoning reinforces the process of learning.

GAZETTE: Why is this strategy an improvement over just learning a single method?

STAR: We think that learning multiple strategies for solving problems deepens students’ understanding of the content. There is a direct benefit to learning through comparing multiple methods, but there are also other types of benefits to students’ motivation. In this process, students come to see math a little differently — not just as a set of problems, each of which has exactly one way to solve it that you must memorize, but rather, as a terrain where there are always decisions to be made and multiple strategies that one might need to justify or debate. Because that is what math is.

For teachers, this can also be empowering because they are interested in increasing their students’ understanding, and we’ve given them a set of tools that can help them do that and potentially make the class more interesting as well. It’s important to note, too, that this approach is not something that we invented. In this case, what we’re asking teachers to do is something that they do a little bit of already. Every high school math teacher, for certain topics, is teaching students multiple strategies. It’s built into the curriculum. All that we’re saying is, first, you should do it more because it’s a good thing, and second, when you do it, this is a certain way that we found to be especially effective, both in terms of the visual materials and the pedagogy. It’s not a big stretch for most teachers. Conversations around ways to teach math for the past 30 or 40 years, and perhaps longer, have been emphasizing the use of multiple strategies.

GAZETTE: What are the potential challenges for math teachers to put this in practice?

STAR: If we want teachers to introduce students to multiple ways to solve problems, we must recognize that that is a lot of information for students and teachers. There is a concern that there could be information overload, and that’s very legitimate. Also, a well-intentioned teacher might take our strategy too far. A teacher might say something like, “Well, if comparing two strategies is good, then why don’t I compare three or four or five?” Not that that’s impossible to do well. But the visual materials you would have to design to help students manage that information overload are quite challenging. We don’t recommend that.

Share this article

You might like.

Seminar foregrounds Harlow Shapley, who helped scholars escape Nazi rule

Ambassador says if Russia is allowed to take over sovereign nation, China may try to do same

Sociologist’s new book finds algorithms that suggest partners often reflect stereotypes, biases

Yes, it’s exciting. Just don’t look at the sun.

Lab, telescope specialist details Harvard eclipse-viewing party, offers safety tips

Forget ‘doomers.’ Warming can be stopped, top climate scientist says

Michael Mann points to prehistoric catastrophes, modern environmental victories

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

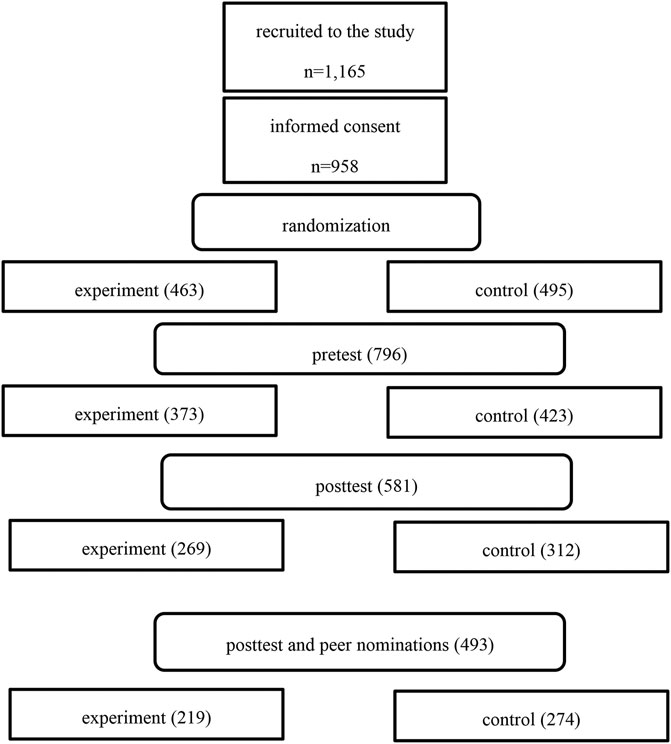
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

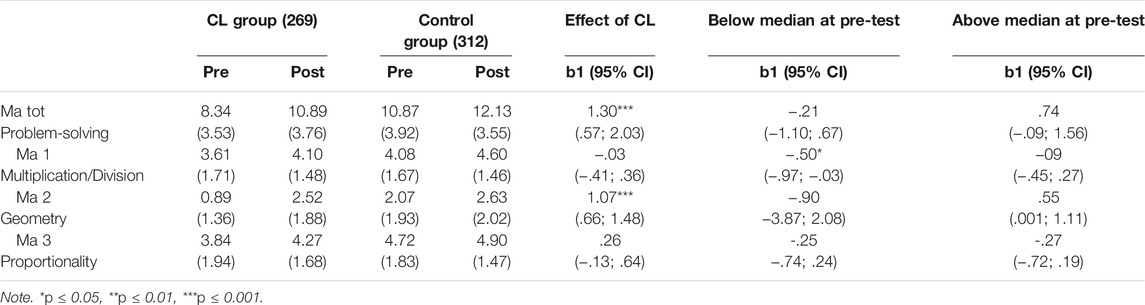
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

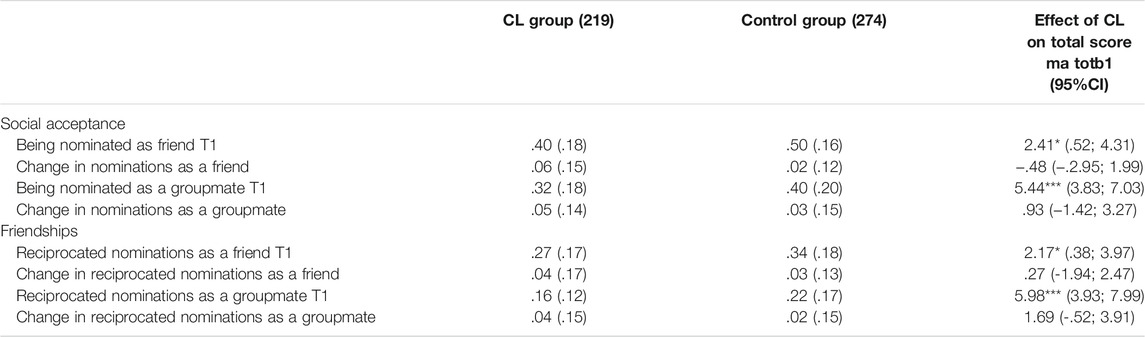
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2013 Revised 2019

Problem Solving and the New Curriculum

• seeking solutions not just memorising procedures
• exploring patterns not just memorising formulas
• formulating conjectures, not just doing exercises.

Noah watched the animals going into the ark. He was counting and by noon he got to $12$, but he was only counting the legs of the animals. How many creatures did he see? See if you can find other answers? Try to tell someone how you found these answers out?

Planning a School Trip

This activity is taken from the ATM publication "We Can Work It Out!", a book of collaborative problem solving activity cards by Anitra Vickery and Mike Spooner. It is available from The Association of Teachers of Mathematics https://www.atm.org.uk/Shop/Primary-Education/Primary-Education-Books/Books--Hardcopy/We-Can-Work-It-Out-1/act054

References Polya, G. 1945) How to Solve It. Princeton University Press Schoenfeld, A.H. (1992) Learning to think mathematically: problem solving, metacognition and sense-making in mathematics. In D.Grouws (ed) Handbook for Research on Mathematics Teaching and Learning (pp334-370) New York: MacMillan

Lampert m (1992) quoted in schoenfeld, above..

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

RESEARCH IN PROBLEM SOLVING IN MATHEMATICS EDUCATION

Related Papers

Kathleen (Kathy) Clark

In this chapter I summarize research and policy recommendations that call for the inclusion of the history of mathematics in the preparation of preservice mathematics teachers (PSTs). Next, I share a model for the course “Using History in the Teaching of Mathematics,” which was designed to encourage PSTs to study and consider including the history of mathematics in teaching. An example of one “topic exploration” from the course is presented.

Samuel Baah-Duodu

ABSTRACT This study measured pre-service teachers’ problem solving abilities (PSA) and their mathematical knowledge for teaching (MKT) basic school mathematics. A Fractional Knowledge Test (FKT) of open ended questions and five- point Likert scale questionnaires were administered to 200 pre-service teachers from two colleges of education (located at Mampong in the Ashanti Region of Ghana) to assess the relationship that exist between problem solving abilities and mathematical knowledge for teaching fractions in basic schools. Pre-service teachers displayed better fractional knowledge on procedure than on conception. The study revealed that pre-service teachers’ problem solving abilities and mathematical knowledge for teaching were low. There was no significant difference by gender, age and mathematical background on pre-service teachers’ problem solving abilities and mathematical knowledge for teaching [MKT]. The study also showed that a strong positive correlation existed between pre-service teachers’ problem solving ability and their mathematical knowledge for teaching [MKT]. Findings indicated that pre-service teachers need adequate opportunities to practice what they learn in their pedagogy courses in colleges. Therefore mathematics pedagogy courses should be made more practical and pre-service teachers in colleges of education should be given ample opportunity to practice what they are going to teach in basic schools. Pre- service teachers need to develop much deeper understandings of the mathematics content than they had as students, and their teachers, mathematics teacher educators, must have the knowledge necessary to help with this development.

Educational Evaluation and Policy Analysis

William Firestone

Ebenezer Tawiah

Mickey Yang

Toivo S Diego Hitewa

This material is of good use to students who are doing business administration

Educational Researcher

Elizabeth Fennema

Douglas H Clements

School Science and Mathematics

Joan Ferrini-Mundy

Robert ADJIAGE

RELATED PAPERS

Verónica Vargas-Alejo

Annual Meeting of the …

Elham Kazemi

Balarabe Yushau

Dana Olanoff

reynaldo estevez

aleksandra veselovsky

Handbook of research on mathematics teaching and …

TUTUL KAIRI

Kathy A Gullie

Chris Briggs-Hale

Publisher ijmra.us UGC Approved

Educational Psychologist

Lindsey Richland

Todd Fennimore

Mathematics Education Library

Gilah Leder , Helen Forgasz

Slagjana Jakimovik

Steven Greenstein

The Mathematics Enthusiast, Special Issue: International Perspectives on Problem Solving Research in Mathematics Education (Manuel Santos-Trigo & Luis Moreno-Armella, Guest Editors), Vol. 10, 1&2 (January 2013), 303-334.

ANNIE SELDEN

… teaching strategies for …

Beatriz D'Ambrosio

Florence Mihaela Singer

Bonny Klaas

Erin Ottmar

Margaret Schroeder

International Group for the Psychology of M athematics …

Ann Gervasoni

Melvin Chan , Ridzuan Rahim

Evan Ortlieb

New ICMI Study Series

Roza Leikin

The Teaching and Learning of Mathematics at University Level: An ICMI Study

John Selden , ANNIE SELDEN

David W Stinson

International Group for the Psychology of …

Hannah Slovin

Yazan Alghazo

Eunice Jang

Laurie D Edwards

Yearbook 2012, Association of Mathematics Educators

Ridzuan Rahim

Professional Development in Education

Nanette Seago , Jennifer Jacobs , Courtney Nelson , Kristen Malzahn

The Story of SUSTAIN

Cadance Lowell

jim de vries

Vicki-Lynn Holmes

"Tertiary mathematics education research and its future," Tennessee Technological University Mathematics Department Technical Report No. 1999-6.

Marcella L. Bullmaster-Day

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

• News Releases

The math problem that took nearly a century to solve

UC San Diego mathematicians unlock the secret to Ramsey numbers

University of California - San Diego

Ramsey problems, such as r(4,5) are simple to state, but as shown in this graph, the possible solutions are nearly endless, making them very difficult to solve. 

Credit: Jacques Verstraete / UC San Diego

We’ve all been there: staring at a math test with a problem that seems impossible to solve. What if finding the solution to a problem took almost a century? For mathematicians who dabble in Ramsey theory, this is very much the case. In fact, little progress had been made in solving Ramsey problems since the 1930s.

Now, University of California San Diego researchers  Jacques Verstraete  and Sam Mattheus have found the answer to r(4,t), a longstanding Ramsey problem that has perplexed the math world for decades.

What was Ramsey’s problem, anyway?

In mathematical parlance, a graph is a series of points and the lines in between those points. Ramsey theory suggests that if the graph is large enough, you’re guaranteed to find some kind of order within it — either a set of points with no lines between them  or  a set of points with all possible lines between them (these sets are called “cliques”). This is written as r(s,t) where  s  are the points with lines and  t  are the points without lines.

To those of us who don’t deal in graph theory, the most well-known Ramsey problem, r(3,3), is sometimes called “the theorem on friends and strangers” and is explained by way of a party: in a group of six people, you will find at least three people who all know each other or three people who all don’t know each other. The answer to r(3,3) is six.

“It’s a fact of nature, an absolute truth,” Verstraete states. “It doesn't matter what the situation is or which six people you pick — you will find three people who all know each other or three people who all don't know each other. You may be able to find more, but you are guaranteed that there will be at least three in one clique or the other.”

What happened after mathematicians found that r(3,3) = 6? Naturally, they wanted to know r(4,4), r(5,5), and r(4,t) where the number of points that are not connected is variable. The solution to r(4,4) is 18 and is proved using a theorem created by Paul Erdös and George Szekeres in the 1930s.

Currently r(5,5) is still unknown.

A good problem fights back

Why is something so simple to state so hard to solve? It turns out to be more complicated than it appears. Let’s say you knew the solution to r(5,5) was somewhere between 40-50. If you started with 45 points, there would be more than 10 234  graphs to consider!

“Because these numbers are so notoriously difficult to find, mathematicians look for estimations,” Verstraete explained. “This is what Sam and I have achieved in our recent work. How do we find not the exact answer, but the best estimates for what these Ramsey numbers might be?”

Math students learn about Ramsey problems early on, so r(4,t) has been on Verstraete’s radar for most of his professional career. In fact, he first saw the problem in print in  Erdös on Graphs: His Legacy of Unsolved Problems,  written by two UC San Diego professors, Fan Chung and the late Ron Graham. The problem is a conjecture from Erdös, who offered $250 to the first person who could solve it.

“Many people have thought about r(4,t) — it’s been an open problem for over 90 years,” Verstraete said. “But it wasn’t something that was at the forefront of my research. Everybody knows it's hard and everyone’s tried to figure it out, so unless you have a new idea, you’re not likely to get anywhere.”

Then about four years ago, Verstraete was working on a different Ramsey problem with a mathematician at the University of Illinois-Chicago, Dhruv Mubayi. Together they discovered that pseudorandom graphs could advance the current knowledge on these old problems.

In 1937, Erdös discovered that using random graphs could give good lower bounds on Ramsey problems. What Verstraete and Mubayi discovered was that sampling from  pseudo random graphs frequently gives better bounds on Ramsey numbers than random graphs. These bounds — upper and lower limits on the possible answer — tightened the range of estimations they could make. In other words, they were getting closer to the truth.

In 2019, to the delight of the math world, Verstraete and Mubayi used pseudorandom graphs to solve r(3,t). However, Verstraete struggled to build a pseudorandom graph that could help solve r(4,t).

He began pulling in different areas of math outside of combinatorics, including finite geometry, algebra and probability. Eventually he joined forces with Mattheus, a postdoctoral scholar in his group whose background was in finite geometry. 

“It turned out that the pseudorandom graph we needed could be found in finite geometry,” Verstraete stated. “Sam was the perfect person to come along and help build what we needed.”

Once they had the pseudorandom graph in place, they still had to puzzle out several pieces of math. It took almost a year, but eventually they realized they had a solution: r(4,t) is close to a cubic function of  t . If you want a party where there will always be four people who all know each other or  t  people who all don’t know each other, you will need roughly t 3  people present. There is a small asterisk (actually an o) because, remember, this is an estimate, not an exact answer. But t 3  is very close to the exact answer.

The findings are currently under review with the  Annals of Mathematics . 

“It really did take us years to solve,” Verstraete stated. “And there were many times where we were stuck and wondered if we’d be able to solve it at all. But one should never give up, no matter how long it takes.”

Verstraete emphasizes the importance of perseverance — something he reminds his students of often. “If you find that the problem is hard and you're stuck, that means it's a good problem. Fan Chung said a good problem fights back. You can't expect it just to reveal itself.”

Verstraete knows such dogged determination is well-rewarded: “I got a call from Fan saying she owes me $250.”

Annals of Mathematics

10.4007/annals.2024.199.2.8

Method of Research

Experimental study

Article Title

The asymptotics of r(4,t)

Article Publication Date

Disclaimer: AAAS and EurekAlert! are not responsible for the accuracy of news releases posted to EurekAlert! by contributing institutions or for the use of any information through the EurekAlert system.

Original Source

The math problem that took nearly a century to solve: Secret to Ramsey numbers

Mathematicians unlock the secret to ramsey numbers.

We've all been there: staring at a math test with a problem that seems impossible to solve. What if finding the solution to a problem took almost a century? For mathematicians who dabble in Ramsey theory, this is very much the case. In fact, little progress had been made in solving Ramsey problems since the 1930s.

Now, University of California San Diego researchers Jacques Verstraete and Sam Mattheus have found the answer to r(4,t), a longstanding Ramsey problem that has perplexed the math world for decades.

What was Ramsey's problem, anyway?

In mathematical parlance, a graph is a series of points and the lines in between those points. Ramsey theory suggests that if the graph is large enough, you're guaranteed to find some kind of order within it -- either a set of points with no lines between them or a set of points with all possible lines between them (these sets are called "cliques"). This is written as r(s,t) where s are the points with lines and t are the points without lines.

To those of us who don't deal in graph theory, the most well-known Ramsey problem, r(3,3), is sometimes called "the theorem on friends and strangers" and is explained by way of a party: in a group of six people, you will find at least three people who all know each other or three people who all don't know each other. The answer to r(3,3) is six.

"It's a fact of nature, an absolute truth," Verstraete states. "It doesn't matter what the situation is or which six people you pick -- you will find three people who all know each other or three people who all don't know each other. You may be able to find more, but you are guaranteed that there will be at least three in one clique or the other."

What happened after mathematicians found that r(3,3) = 6? Naturally, they wanted to know r(4,4), r(5,5), and r(4,t) where the number of points that are not connected is variable. The solution to r(4,4) is 18 and is proved using a theorem created by Paul Erdös and George Szekeres in the 1930s.

Currently r(5,5) is still unknown.

A good problem fights back

Why is something so simple to state so hard to solve? It turns out to be more complicated than it appears. Let's say you knew the solution to r(5,5) was somewhere between 40-50. If you started with 45 points, there would be more than 10 234 graphs to consider!

"Because these numbers are so notoriously difficult to find, mathematicians look for estimations," Verstraete explained. "This is what Sam and I have achieved in our recent work. How do we find not the exact answer, but the best estimates for what these Ramsey numbers might be?"

Math students learn about Ramsey problems early on, so r(4,t) has been on Verstraete's radar for most of his professional career. In fact, he first saw the problem in print in Erdös on Graphs: His Legacy of Unsolved Problems, written by two UC San Diego professors, Fan Chung and the late Ron Graham. The problem is a conjecture from Erdös, who offered $250 to the first person who could solve it.

"Many people have thought about r(4,t) -- it's been an open problem for over 90 years," Verstraete said. "But it wasn't something that was at the forefront of my research. Everybody knows it's hard and everyone's tried to figure it out, so unless you have a new idea, you're not likely to get anywhere."

Then about four years ago, Verstraete was working on a different Ramsey problem with a mathematician at the University of Illinois-Chicago, Dhruv Mubayi. Together they discovered that pseudorandom graphs could advance the current knowledge on these old problems.

In 1937, Erdös discovered that using random graphs could give good lower bounds on Ramsey problems. What Verstraete and Mubayi discovered was that sampling from pseudo random graphs frequently gives better bounds on Ramsey numbers than random graphs. These bounds -- upper and lower limits on the possible answer -- tightened the range of estimations they could make. In other words, they were getting closer to the truth.

In 2019, to the delight of the math world, Verstraete and Mubayi used pseudorandom graphs to solve r(3,t). However, Verstraete struggled to build a pseudorandom graph that could help solve r(4,t).

He began pulling in different areas of math outside of combinatorics, including finite geometry, algebra and probability. Eventually he joined forces with Mattheus, a postdoctoral scholar in his group whose background was in finite geometry.

"It turned out that the pseudorandom graph we needed could be found in finite geometry," Verstraete stated. "Sam was the perfect person to come along and help build what we needed."

Once they had the pseudorandom graph in place, they still had to puzzle out several pieces of math. It took almost a year, but eventually they realized they had a solution: r(4,t) is close to a cubic function of t . If you want a party where there will always be four people who all know each other or t people who all don't know each other, you will need roughly t 3 people present. There is a small asterisk (actually an o) because, remember, this is an estimate, not an exact answer. But t 3 is very close to the exact answer.

The findings are currently under review with the Annals of Mathematics .

"It really did take us years to solve," Verstraete stated. "And there were many times where we were stuck and wondered if we'd be able to solve it at all. But one should never give up, no matter how long it takes."

Verstraete emphasizes the importance of perseverance -- something he reminds his students of often. "If you find that the problem is hard and you're stuck, that means it's a good problem. Fan Chung said a good problem fights back. You can't expect it just to reveal itself."

Verstraete knows such dogged determination is well-rewarded: "I got a call from Fan saying she owes me $250."

• Mathematics
• Math Puzzles
• Mathematical Modeling
• Educational Technology
• Computer Modeling
• Distributed Computing
• Quantum computer
• Knot theory
• Massively multiplayer online game
• Supercomputer
• Algebraic geometry
• John von Neumann
• Scientific method

Story Source:

Materials provided by University of California - San Diego . Original written by Michelle Franklin. Note: Content may be edited for style and length.

Journal Reference :

• Sam Mattheus, Jacques Verstraete. The asymptotics of r(4,t) . Annals of Mathematics , 2024; 199 (2) DOI: 10.4007/annals.2024.199.2.8

Cite This Page :

Explore More

• Pregnancy Accelerates Biological Aging
• Tiny Plastic Particles Are Found Everywhere
• What's Quieter Than a Fish? A School of Them
• Do Odd Bones Belong to Gigantic Ichthyosaurs?
• Big-Eyed Marine Worm: Secret Language?
• Unprecedented Behavior from Nearby Magnetar
• Soft, Flexible 'Skeletons' for 'Muscular' Robots
• Toothed Whale Echolocation and Jaw Muscles
• Friendly Pat On the Back: Free Throws
• How the Moon Turned Itself Inside Out

Trending Topics

Strange & offbeat.

Tseng’s extragradient method with double projection for solving pseudomonotone variational inequality problems in Hilbert spaces

• Published: 10 April 2024
• Volume 43 , article number  171 , ( 2024 )

Cite this article

• Zhongbing Xie 1 ,
• Gang Cai   ORCID: orcid.org/0000-0002-0659-0203 2 ,
• Xiaoxiao Li 3 &
• Qiao-Li Dong 3  

The aim of this paper is to investigate an accelerated Tseng’s extragradient method with double projection for solving Lipschitzian and pseudomonotone variational inequalities in real Hilbert spaces. A strong convergence theorem of the proposed algorithm is obtained under some appropriate assumptions imposed on the parameters. Finally, we give some numerical examples to demonstrate the performance of our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

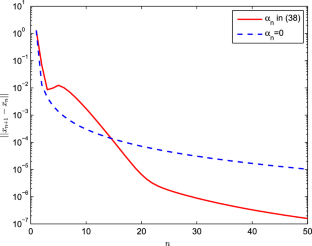
Data availability statement

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Anh PK, Thong DV, Vinh NT (2022) Improved inertial extragradient methods for solving pseudo-monotone variational inequalities. Optimization 71:505–528

Article   MathSciNet   Google Scholar  

Antipin AS (1976) On a method for convex programs using a symmetrical modification of the Lagrange function. Ekonomika i Mat. Metody 12:1164–1173

Google Scholar  

Aubin JP, Ekeland I (1984) Applied Nonlinear Analysis. Wiley, New York

Baiocchi C, Capelo A (1984) Variational and Quasivariational Inequalities. Applications to Free Boundary Problems. Wiley, New York

Bot RI, Csetnek ER (2016) An inertial Tseng’s type proximal algorithm for nonsmooth and nonconvex optimization problems. J Optim Theory Appl 171:600–616

Bot RI, Hendrich C (2013) A Douglas-Rachford type primal-dual method for solving inclusions with mixtures of composite and parallel-sum type monotone operators. SIAM J Optim 23(4):2541–2565

Bot RI, Csetnek ER, Heinrich A (2013) A primal-dual splitting algorithm for finding zeros of sums of maximally monotone operators. SIAM J Optim 23(4):2011–2036

Bot RI, Csetnek ER, Heinrich A, Hendrich C (2015a) On the convergence rate improvement of a primal-dual splitting algorithm for solving monotone inclusion problems. Math Program 150:251–279

Bot RI, Csetnek ER, Hendrich C (2015b) Inertial Douglas-Rachford splitting for monotone inclusion. Appl Math Comput 256:472–487

Cai G, Shehu Y, Iyiola OS (2019) The modified viscosity implicit rules for variational inequality problems and fixed point problems of nonexpansive mappings in Hilbert spaces. Rev R Acad Cienc Exactas Fís Nat Ser A Mat RACSAM 113:3545–3562

Cai G, Shehu Y, Iyiola OS (2017) Modified viscosity implicit rules for nonexpansive mappings in Hilbert spaces. J Fixed Point Theory Appl 19:2831–2846

Cai G, Gibali A, Iyiola OS, Shehu Y (2018) A new double-projection method for solving variational inequalities in Banach spaces. J Optim Theory Appl 178:219–239

Cao Y, Guo K (2020) On the covergence of inertial two-subgradient extragradient method for variational inequality problems. Optimization 69:1237–1253

Censor Y, Gibali A, Reich S (2011) The subgradient extragradient method for solving variational inequalities in Hilbert space. J Optim Theory Appl 148:318–335

Censor Y, Gibali A, Reich S (2011) Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim Meth Softw 26:827–845

Censor Y, Gibali A, Reich S (2011) Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space. Optimization 61:1119–1132

Censor Y, Gibali A, Reich S (2012) Algorithms for the split variational inequality problem. Numer Algorithms 56:301–323

Cholamjiak P, Thong DV, Cho YJ (2020) A novel inertial projection and contraction method for solving pseudomonotone variational inequality problems. Acta Appl Math 169:217–245

Cottle RW, Yao JC (1992) Pseudo-monotone complementarity problems in Hilbert space. J Optim Theory Appl 75:281–295

Denisov SV, Semenov VV, Chabak LM (2015) Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators. Cybern Syst Anal 51:757–765

Facchinei F, Pang JS (2003) Finite-Dimensional Variational Inequalities and Complementarity Problems, vol I. Springer Series in Operations Research. Springer, New York

Fichera G (1963) Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad Naz Lincei 34:138–142

MathSciNet   Google Scholar  

Fichera G (1964) Problemi elastostatici con vincoli unilaterali: il problema di Signorini con ambigue condizioni al contorno. Atti Accad Naz Lincei 7:91–140

Glowinski R, Lions JL, Trémolières R (1981) Numerical Analysis of Variational Inequalities. Elsevier, Amsterdam

Goebel K, Reich S (1984) Uniform convexity, hyperbolic geometry and nonexpansive mappings. Marcel Dekker, New York

Iiduka H, Takahashi W, Toyoda M (2004) Approximation of solutions of variational inequalities for monotone mappings. Pan Math J 14:49–61

Iusem AN, Nasri M (2011) Korpelevich’s method for variational inequality problems in Banach spaces. J Glob Optim 50:59–76

Iusem AN, Svaiter BF (1997) A variant of Korpelevich’s method for variational inequalities with a new search strategy. Optimization 42:309–321

Kassay G, Reich S, Sabach S (2011) Iterative methods for solving systems of variational inequalities in refelexive Banach spaces. SIAM J Optim 21:1319–1344

Kinderlehrer D, Stampacchia G (1980) An Introduction to Variational Inequalities and Their Applications. Academic Press, New York

Konnov IV (2001) Combined Relaxation Methods for Variational Inequalities. Springer, Berlin

Book   Google Scholar  

Korpelevich GM (1976) The extragradient method for finding saddle points and other problems. Ekonomika i Mat Metody 12:747–756

Kraikaew R, Saejung S (2014) Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces. J Optim Theory Appl 163:399–412

Liu LS (1995) Ishikawa and Mann iteration process with errors for nonlinear strongly accretive mappings in Banach spaces. J Math Anal Appl 194:114–125

Maingé PE (2008) A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J Control Optim 47:1499–1515

Malitsky YV (2015) Projected reflected gradient methods for monotone variational inequalities. SIAM J Optim 25:502–520

Malitsky YV, Semenov VV (2015) A hybrid method without extrapolation step for solving variational inequality problems. J Glob Optim 61:193–202

Marcotte P (1991) Applications of Khobotov’s algorithm to variational and network equlibrium problems. Inf Syst Oper Res 29:258–270

Noor MA (2004) Some development in general variational inequalities. Appl Math Comput 152:199–277

Noor MA (2008) On iterative methods for solving a system of mixed variational inequalities. Appl Anal 87:99–108

Reich S (1979) Constructive Techniques for Accretive and Monotone Operators. Applied Nonlinear Analysis. Academic Press, New York

Solodov MV, Svaiter BF (1999) A new projection method for variational inequality problems. SIAM J Control Optim 37:765–776

Suantai S, Pholasa N, Cholamjiak P (2018) The modified inertial relaxed CQ algorithm for solving the split feasibility problems. J Ind Manag Optim 14:1595–1615

Thong DV, Hieu DV (2018) Modified subgradient extragradient method for variational inequality problems. Numer Algorithms 79:597–610

Thong DV, Hieu DV (2018) Modified Tseng’s extragradient algorithms for variational inequality problems. J Fixed Point Theory Appl 20:152

Thong DV, Vinh NT, Cho YJ (2019) Accelerated subgradient extragradient methods for variational inequality problems. J Sci Comput 80:1438–1462

Thong DV, Vinh NT, Cho YJ (2020) A strong convergence theorem for Tseng’s extragradient method for solving variational inequality problems. Optim Lett 14:1157–1175

Tseng P (2000) A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim 38:431–446

Vuong PT, Shehu Y (2019) Convergence of an extragradient-type method for variational inequality with applications to optimal control problems. Numer Algor 81:269–291

Xie Z, Cai G, Li X, Dong QL (2023) A new self adaptive Tseng’s extragradient method with double-projection for solving pseudomonotone variational inequality problems in Hilbert spaces. Int J Nonlinear Sci Numer Simul 24:539–554

Xu HK (2002) Iterative algorithms for nonlinear operators. J Lond Math Soc 66:240–256

Yao Y, Noor MA (2007) On viscosity iterative methods for variational inequalities. J Math Anal Appl 325:776–787

Zhu DL, Marcotte P (1996) Co-coercivity and its role in the convergence of iterative schemes for solving variational inequalities. SIAM J Optim 6:714–726

Download references

Acknowledgements

This work was supported by the Natural Science Foundation of China (Grant No. 12171062), the Natural Science Foundation of Chongqing (Grant No. CSTB2022NSCQJQX0004), the Chongqing Talent Support program (Grant No. cstc2024ycjhbgzxm0121) and Science and Technology Project of Chongqing Education Committee (Grant No. KJZD-M202300503).

Author information

Authors and affiliations.

School of Mathematics and Statistics, Wuhan University, Wuhan, 430072, China

Zhongbing Xie

School of Mathematical Sciences, Chongqing Normal University, Chongqing, 401331, China

College of Science, Civil Aviation University of China, Tianjin, 300300, China

Xiaoxiao Li & Qiao-Li Dong

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gang Cai .

Ethics declarations

Conflict of interest.

The authors declare that they have no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Xie, Z., Cai, G., Li, X. et al. Tseng’s extragradient method with double projection for solving pseudomonotone variational inequality problems in Hilbert spaces. Comp. Appl. Math. 43 , 171 (2024). https://doi.org/10.1007/s40314-024-02698-3

Download citation

Received : 18 November 2022

Revised : 13 March 2024

Accepted : 14 March 2024

Published : 10 April 2024

DOI : https://doi.org/10.1007/s40314-024-02698-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Strong convergence
• Tseng’s extragradient method
• Inertial method
• Variational inequality
• Pseudomonotone operator

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research