matrix representation graph

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials

Graph and its representations

• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring
• Traveling Salesman Problem (TSP) Implementation
• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

What is Graph Data Structure?

A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E) .

Representations of Graph

Here are the two most common ways to represent a graph :

Adjacency Matrix

Adjacency list.

An adjacency matrix is a way of representing a graph as a matrix of boolean (0’s and 1’s).

Let’s assume there are n vertices in the graph So, create a 2D matrix adjMat[n][n] having dimension n x n.

If there is an edge from vertex i to j , mark adjMat[i][j] as 1 . If there is no edge from vertex i to j , mark adjMat[i][j] as 0 .

Representation of Undirected Graph to Adjacency Matrix:

The below figure shows an undirected graph. Initially, the entire Matrix is ​​initialized to 0 . If there is an edge from source to destination, we insert 1 to both cases ( adjMat[destination] and adjMat [ destination]) because we can go either way.

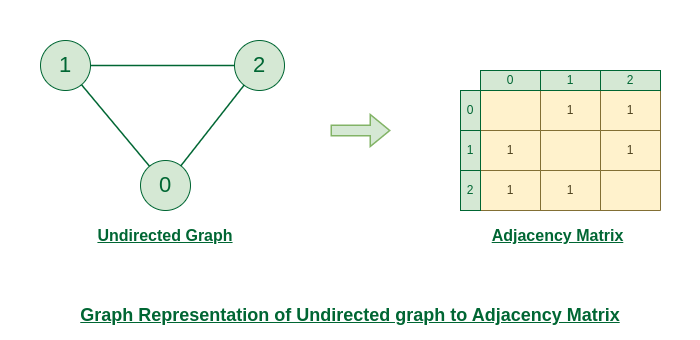
Undirected Graph to Adjacency Matrix

Representation of Directed Graph to Adjacency Matrix:

The below figure shows a directed graph. Initially, the entire Matrix is ​​initialized to 0 . If there is an edge from source to destination, we insert 1 for that particular adjMat[destination] .

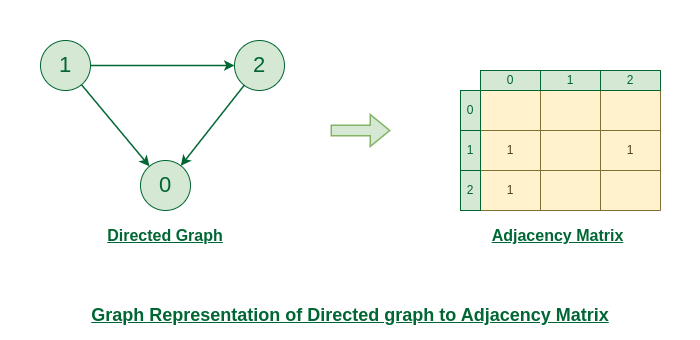
Directed Graph to Adjacency Matrix

An array of Lists is used to store edges between two vertices. The size of array is equal to the number of vertices (i.e, n) . Each index in this array represents a specific vertex in the graph. The entry at the index i of the array contains a linked list containing the vertices that are adjacent to vertex i .

Let’s assume there are n vertices in the graph So, create an array of list of size n as adjList[n].

adjList[0] will have all the nodes which are connected (neighbour) to vertex 0 . adjList[1] will have all the nodes which are connected (neighbour) to vertex 1 and so on.

Representation of Undirected Graph to Adjacency list:

The below undirected graph has 3 vertices. So, an array of list will be created of size 3, where each indices represent the vertices. Now, vertex 0 has two neighbours (i.e, 1 and 2). So, insert vertex 1 and 2 at indices 0 of array. Similarly, For vertex 1, it has two neighbour (i.e, 2 and 0) So, insert vertices 2 and 0 at indices 1 of array. Similarly, for vertex 2, insert its neighbours in array of list.

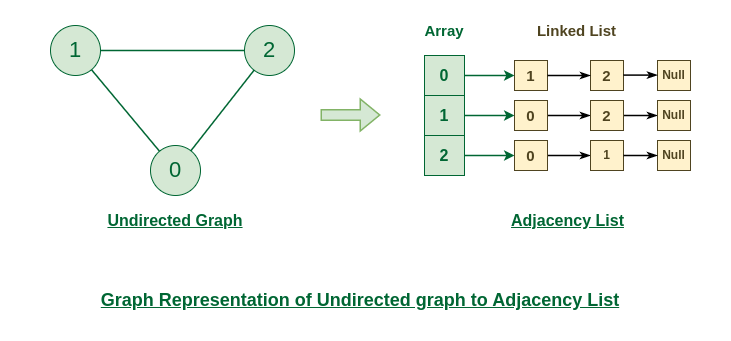
Undirected Graph to Adjacency list

Representation of Directed Graph to Adjacency list:

The below directed graph has 3 vertices. So, an array of list will be created of size 3, where each indices represent the vertices. Now, vertex 0 has no neighbours. For vertex 1, it has two neighbour (i.e, 0 and 2) So, insert vertices 0 and 2 at indices 1 of array. Similarly, for vertex 2, insert its neighbours in array of list.

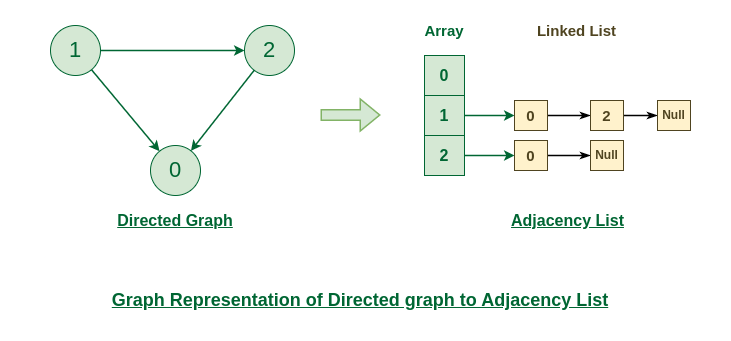
Directed Graph to Adjacency list

Please Login to comment...

• graph-basics
• 10 Best Free Social Media Management and Marketing Apps for Android - 2024
• 10 Best Customer Database Software of 2024
• How to Delete Whatsapp Business Account?
• Discord vs Zoom: Select The Efficienct One for Virtual Meetings?
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Trending Categories

• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Matrix Representation of Graphs

A graph can be represented using Adjacency Matrix way.

Adjacency Matrix

An Adjacency Matrix A[V][V] is a 2D array of size V × V where $V$ is the number of vertices in a undirected graph. If there is an edge between V x to V y then the value of A[V x ][V y ]=1 and A[V y ][V x ]=1, otherwise the value will be zero.

For a directed graph, if there is an edge between V x to V y , then the value of A[V x ][V y ]=1, otherwise the value will be zero.

Adjacency Matrix of an Undirected Graph

Let us consider the following undirected graph and construct the adjacency matrix −

Adjacency matrix of the above undirected graph will be −

Adjacency Matrix of a Directed Graph

Let us consider the following directed graph and construct its adjacency matrix −

Adjacency matrix of the above directed graph will be −

Related Articles

• Representation of Graphs
• Convert Adjacency Matrix to Adjacency List Representation of Graph
• Add and Remove Vertex in Adjacency Matrix Representation of Graph
• Prim’s Algorithm (Simple Implementation for Adjacency Matrix Representation) in C++
• Basic Concepts of Graphs
• Representation of fractions
• Isomorphism and Homeomorphism of graphs
• Planar Graphs
• Bipartite Graphs
• Eulerian Graphs
• Hamiltonian Graphs
• Successor Graphs
• Strongly Connected Graphs
• Speed Time Graphs
• Representation of Relations using Graph

Kickstart Your Career

Get certified by completing the course

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.1: Representing a Graph by a Matrix

• Last updated
• Save as PDF
• Page ID 8485

• Carleton University via Athabasca University Press

An adjacency matrix is a way of representing an \(\mathtt{n}\) vertex graph \(G=(V,E)\) by an \(\mathtt{n}\times\mathtt{n}\) matrix, \(\mathtt{a}\), whose entries are boolean values.

The matrix entry \(\mathtt{a[i][j]}\) is defined as

\[\mathtt{a[i][j]}= \begin{cases} \mathtt{true} & \text{if } \mathtt{(i,j)}\in E \\ \mathtt{false} & \text{otherwise} \end{cases}\nonumber\]

The adjacency matrix for the graph in Figure 12.1 is shown in Figure \(\PageIndex{1}\).

In this representation, the operations \(\mathtt{addEdge(i,j)}\), \(\mathtt{removeEdge(i,j)}\), and \(\mathtt{hasEdge(i,j)}\) just involve setting or reading the matrix entry \(\mathtt{a[i][j]}\):

These operations clearly take constant time per operation.

Where the adjacency matrix performs poorly is with the \(\mathtt{outEdges(i)}\) and \(\mathtt{inEdges(i)}\) operations. To implement these, we must scan all \(\mathtt{n}\) entries in the corresponding row or column of \(\mathtt{a}\) and gather up all the indices, \(\mathtt{j}\), where \(\mathtt{a[i][j]}\), respectively \(\mathtt{a[j][i]}\), is true.

These operations clearly take \(O(\mathtt{n})\) time per operation.

Another drawback of the adjacency matrix representation is that it is large. It stores an \(\mathtt{n}\times \mathtt{n}\) boolean matrix, so it requires at least \(\mathtt{n}^2\) bits of memory. The implementation here uses a matrix of \(\mathtt{boolean}\) values so it actually uses on the order of \(\mathtt{n}^2\) bytes of memory. A more careful implementation, which packs \(\mathtt{w}\) boolean values into each word of memory, could reduce this space usage to \(O(\mathtt{n}^2/\mathtt{w})\) words of memory.

Theorem \(\PageIndex{1}\)

The AdjacencyMatrix data structure implements the Graph interface. An AdjacencyMatrix supports the operations

• \(\mathtt{addEdge(i,j)}\), \(\mathtt{removeEdge(i,j)}\), and \(\mathtt{hasEdge(i,j)}\) in constant time per operation; and
• \(\mathtt{inEdges(i)}\), and \(\mathtt{outEdges(i)}\) in \(O(\mathtt{n})\) time per operation.

The space used by an AdjacencyMatrix is \(O(\mathtt{n}^2)\).

Despite its high memory requirements and poor performance of the \(\mathtt{inEdges(i)}\) and \(\mathtt{outEdges(i)}\) operations, an AdjacencyMatrix can still be useful for some applications. In particular, when the graph \(G\) is dense , i.e., it has close to \(\mathtt{n}^2\) edges, then a memory usage of \(\mathtt{n}^2\) may be acceptable.

The AdjacencyMatrix data structure is also commonly used because algebraic operations on the matrix \(\mathtt{a}\) can be used to efficiently compute properties of the graph \(G\). This is a topic for a course on algorithms, but we point out one such property here: If we treat the entries of \(\mathtt{a}\) as integers (1 for \(\mathtt{true}\) and 0 for \(\mathtt{false}\)) and multiply \(\mathtt{a}\) by itself using matrix multiplication then we get the matrix \(\mathtt{a}^2\). Recall, from the definition of matrix multiplication, that

\[\mathtt{a^2[i][j]} = \sum_{k=0}^{\mathtt{n}-1} \mathtt{a[i][k]}\cdot \mathtt{a[k][j]} \enspace .\nonumber\]

Interpreting this sum in terms of the graph \(G\), this formula counts the number of vertices, \(\mathtt{k}\), such that \(G\) contains both edges \(\mathtt{(i,k)}\) and \(\mathtt{(k,j)}\). That is, it counts the number of paths from \(\mathtt{i}\) to \(\mathtt{j}\) (through intermediate vertices, \(\mathtt{k}\)) whose length is exactly two. This observation is the foundation of an algorithm that computes the shortest paths between all pairs of vertices in \(G\) using only \(O(\log \mathtt{n})\) matrix multiplications.

Learn Python practically and Get Certified .

Popular Tutorials

Popular examples, reference materials, learn python interactively, dsa introduction.

• What is an algorithm?
• Data Structure and Types
• Why learn DSA?
• Asymptotic Notations
• Master Theorem
• Divide and Conquer Algorithm

Data Structures (I)

• Types of Queue
• Circular Queue
• Priority Queue

Data Structures (II)

• Linked List
• Linked List Operations
• Types of Linked List
• Heap Data Structure
• Fibonacci Heap
• Decrease Key and Delete Node Operations on a Fibonacci Heap

Tree based DSA (I)

• Tree Data Structure
• Tree Traversal
• Binary Tree
• Full Binary Tree
• Perfect Binary Tree
• Complete Binary Tree
• Balanced Binary Tree
• Binary Search Tree

Tree based DSA (II)

• Insertion in a B-tree
• Deletion from a B-tree
• Insertion on a B+ Tree
• Deletion from a B+ Tree
• Red-Black Tree
• Red-Black Tree Insertion
• Red-Black Tree Deletion

Graph based DSA

• Graph Data Structure
• Spanning Tree
• Strongly Connected Components

Adjacency Matrix

Adjacency List

• DFS Algorithm
• Breadth-first Search
• Bellman Ford's Algorithm

Sorting and Searching Algorithms

• Bubble Sort
• Selection Sort
• Insertion Sort
• Counting Sort
• Bucket Sort
• Linear Search
• Binary Search

Greedy Algorithms

• Greedy Algorithm
• Ford-Fulkerson Algorithm
• Dijkstra's Algorithm
• Kruskal's Algorithm
• Prim's Algorithm
• Huffman Coding
• Dynamic Programming
• Floyd-Warshall Algorithm
• Longest Common Sequence

Other Algorithms

• Backtracking Algorithm
• Rabin-Karp Algorithm

DSA Tutorials

Graph Data Stucture

Depth First Search (DFS)

Breadth first search

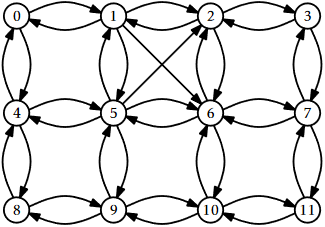
An adjacency matrix is a way of representing a graph as a matrix of booleans (0's and 1's). A finite graph can be represented in the form of a square matrix on a computer, where the boolean value of the matrix indicates if there is a direct path between two vertices.

For example, we have a graph below.

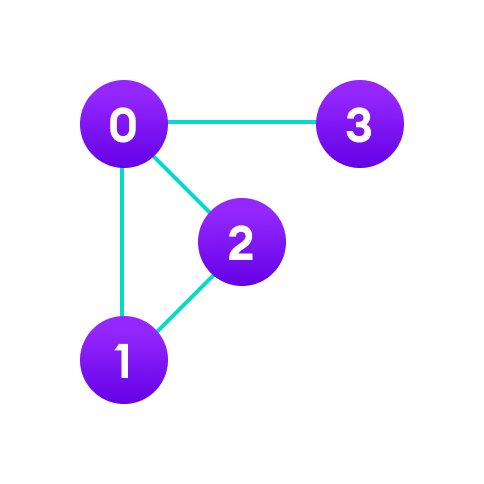
We can represent this graph in matrix form like below.

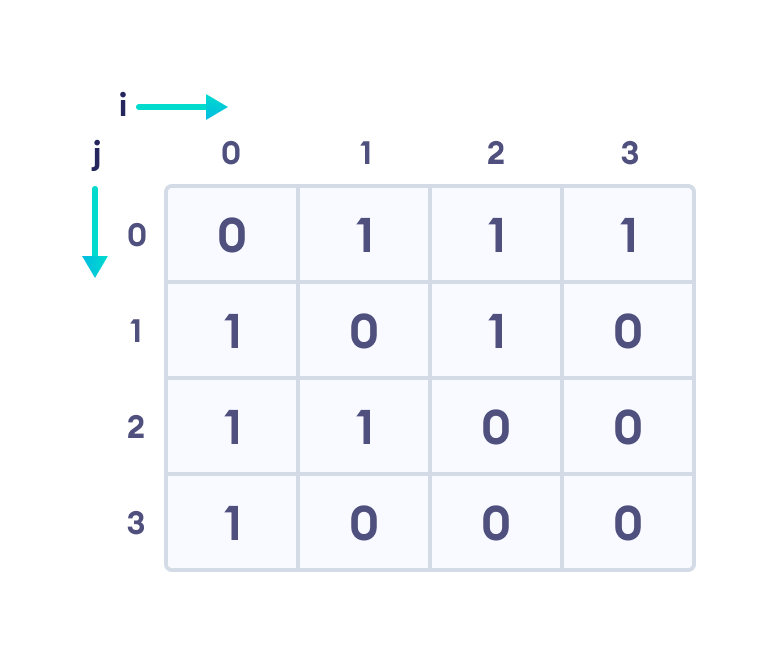
Each cell in the above table/matrix is represented as A ij , where i and j are vertices. The value of A ij is either 1 or 0 depending on whether there is an edge from vertex i to vertex j .

If there is a path from i to j , then the value of A ij is 1 otherwise its 0. For instance, there is a path from vertex 1 to vertex 2, so A 12 is 1 and there is no path from vertex 1 to 3, so A 13 is 0.

In case of undirected graphs, the matrix is symmetric about the diagonal because of every edge (i,j) , there is also an edge (j,i) .

• Pros of Adjacency Matrix
• The basic operations like adding an edge, removing an edge, and checking whether there is an edge from vertex i to vertex j are extremely time efficient, constant time operations.
• If the graph is dense and the number of edges is large, an adjacency matrix should be the first choice. Even if the graph and the adjacency matrix is sparse, we can represent it using data structures for sparse matrices.
• The biggest advantage, however, comes from the use of matrices. The recent advances in hardware enable us to perform even expensive matrix operations on the GPU.
• By performing operations on the adjacent matrix, we can get important insights into the nature of the graph and the relationship between its vertices.
• Cons of Adjacency Matrix
• The VxV space requirement of the adjacency matrix makes it a memory hog. Graphs out in the wild usually don't have too many connections and this is the major reason why adjacency lists are the better choice for most tasks.
• While basic operations are easy, operations like inEdges and outEdges are expensive when using the adjacency matrix representation.
• Adjacency Matrix Code in Python, Java, and C/C++

If you know how to create two-dimensional arrays, you also know how to create an adjacency matrix.

• Adjacency Matrix Applications
• Creating routing table in networks
• Navigation tasks

Table of Contents

• Introduction

Sorry about that.

Related Tutorials

DS & Algorithms

Matrix Representation on Graphs

• First Online: 01 January 2012

Cite this chapter

• Santanu Saha Ray 2  

5643 Accesses

Let us consider a graph G in Fig.  6.1 with four vertices and five edges \( e_{1} ,e_{2} ,e_{3} ,e_{4} ,e_{5} . \) Any subgraph H of G can be represented by a 5-tuple.

Graph G and its two subgraphs H 1 and H 2

• Circuit Matrix
• Incidence Matrix
• Cycle Matrix
• Fundamental Circuit
• Reference Vertex

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

A vector space is n -dimensional if the maximum number of linearly independent vectors in the space is n . If a vector space V has a basis \( \beta \; = \;\left\{ {b_{1} ,b_{2} , \ldots ,b_{n} } \right\}, \) then any set in V containing more than n vectors must be linearly dependent.

Author information

Authors and affiliations.

Department of Mathematics, National Institute of Technology Rourkela, Rourkela, Orissa, 769008, India

Santanu Saha Ray

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Santanu Saha Ray .

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer India

About this chapter

Saha Ray, S. (2013). Matrix Representation on Graphs. In: Graph Theory with Algorithms and its Applications. Springer, India. https://doi.org/10.1007/978-81-322-0750-4_6

Download citation

DOI : https://doi.org/10.1007/978-81-322-0750-4_6

Published : 02 November 2012

Publisher Name : Springer, India

Print ISBN : 978-81-322-0749-8

Online ISBN : 978-81-322-0750-4

eBook Packages : Engineering Engineering (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research