mathematical problem solving wilson

Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. Such experiences at a susceptible age may create a taste for mental work and leave their imprint on mind and character for a lifetime. (26, p. v.)

Problem solving has a special importance in the study of mathematics. A primary goal of mathematics teaching and learning is to develop the ability to solve a wide variety of complex mathematics problems. Stanic and Kilpatrick (43) traced the role of problem solving in school mathematics and illustrated a rich history of the topic. To many mathematically literate people, mathematics is synonymous with solving problems -- doing word problems, creating patterns, interpreting figures, developing geometric constructions, proving theorems, etc. On the other hand, persons not enthralled with mathematics may describe any mathematics activity as problem solving.

Learning to solve problems is the principal reason for studying mathematics.

National Council of Supervisors of Mathematics (22)

When two people talk about mathematics problem solving, they may not be talking about the same thing. The rhetoric of problem solving has been so pervasive in the mathematics education of the 1980s and 1990s that creative speakers and writers can put a twist on whatever topic or activity they have in mind to call it problem solving! Every exercise of problem solving research has gone through some agony of defining mathematics problem solving. Yet, words sometimes fail. Most people resort to a few examples and a few nonexamples. Reitman (29) defined a problem as when you have been given the description of something but do not yet have anything that satisfies that description. Reitman's discussion described a problem solver as a person perceiving and accepting a goal without an immediate means of reaching the goal. Henderson and Pingry (11) wrote that to be problem solving there must be a goal, a blocking of that goal for the individual, and acceptance of that goal by the individual. What is a problem for one student may not be a problem for another -- either because there is no blocking or no acceptance of the goal. Schoenfeld (33) also pointed out that defining what is a problem is always relative to the individual.

How long is the groove on one side of a long-play (33 1/3 rpm) phonograph record? Assume there is a single recording and the Outer (beginning) groove is 5.75 inches from the center and the Inner (ending) groove is 1.75 inches from the center. The recording plays for 23 minutes.

Research on Problem Solving

Educational research is conducted within a variety of constraints -- isolation of variables, availability of subjects, limitations of research procedures, availability of resources, and balancing of priorities. Various research methodologies are used in mathematics education research including a clinical approach that is frequently used to study problem solving. Typically, mathematical tasks or problem situations are devised, and students are studied as they perform the tasks. Often they are asked to talk aloud while working or they are interviewed and asked to reflect on their experience and especially their thinking processes. Waters (48) discusses the advantages and disadvantages of four different methods of measuring strategy use involving a clinical approach. Schoenfeld (32) describes how a clinical approach may be used with pairs of students in an interview. He indicates that "dialog between students often serves to make managerial decisions overt, whereas such decisions are rarely overt in single student protocols."

A nine-digit number is formed using each of the digits 1,2,3,...,9 exactly once. For n = 1,2,3,...,9, n divides the first n digits of the number. Find the number.

The basis for most mathematics problem solving research for secondary school students in the past 31 years can be found in the writings of Polya (26,27,28), the field of cognitive psychology, and specifically in cognitive science. Cognitive psychologists and cognitive scientists seek to develop or validate theories of human learning (9) whereas mathematics educators seek to understand how their students interact with mathematics (33,40). The area of cognitive science has particularly relied on computer simulations of problem solving (25,50). If a computer program generates a sequence of behaviors similar to the sequence for human subjects, then that program is a model or theory of the behavior. Newell and Simon (25), Larkin (18), and Bobrow (2) have provided simulations of mathematical problem solving. These simulations may be used to better understand mathematics problem solving.

Constructivist theories have received considerable acceptance in mathematics education in recent years. In the constructivist perspective, the learner must be actively involved in the construction of one's own knowledge rather than passively receiving knowledge. The teacher's responsibility is to arrange situations and contexts within which the learner constructs appropriate knowledge (45,48). Even though the constructivist view of mathematics learning is appealing and the theory has formed the basis for many studies at the elementary level, research at the secondary level is lacking. Our review has not uncovered problem solving research at the secondary level that has its basis in a constructivist perspective. However, constructivism is consistent with current cognitive theories of problem solving and mathematical views of problem solving involving exploration, pattern finding, and mathematical thinking (36,15,20); thus we urge that teachers and teacher educators become familiar with constructivist views and evaluate these views for restructuring their approaches to teaching, learning, and research dealing with problem solving.

A Framework

Clearly, the linear nature of the models used in numerous textbooks does not promote the spirit of Polya's stages and his goal of teaching students to think. By their nature, all of these traditional models have the following defects:

1. They depict problem solving as a linear process. 2. They present problem solving as a series of steps. 3. They imply that solving mathematics problems is a procedure to be memorized, practiced, and habituated. 4. They lead to an emphasis on answer getting.

These linear formulations are not very consistent with genuine problem solving activity. They may, however, be consistent with how experienced problem solvers present their solutions and answers after the problem solving is completed. In an analogous way, mathematicians present their proofs in very concise terms, but the most elegant of proofs may fail to convey the dynamic inquiry that went on in constructing the proof.

Another aspect of problem solving that is seldom included in textbooks is problem posing, or problem formulation. Although there has been little research in this area, this activity has been gaining considerable attention in U. S. mathematics education in recent years. Brown and Walter (3) have provided the major work on problem posing. Indeed, the examples and strategies they illustrate show a powerful and dynamic side to problem posing activities. Polya (26) did not talk specifically about problem posing, but much of the spirit and format of problem posing is included in his illustrations of looking back.

A framework is needed that emphasizes the dynamic and cyclic nature of genuine problem solving. A student may begin with a problem and engage in thought and activity to understand it. The student attempts to make a plan and in the process may discover a need to understand the problem better. Or when a plan has been formed, the student may attempt to carry it out and be unable to do so. The next activity may be attempting to make a new plan, or going back to develop a new understanding of the problem, or posing a new (possibly related) problem to work on.

Problem solving abilities, beliefs, attitudes, and performance develop in contexts (36) and those contexts must be studied as well as specific problem solving activities. We have chosen to organize the remainder of this chapter around the topics of problem solving as a process, problem solving as an instructional goal, problem solving as an instructional method, beliefs about problem solving, evaluation of problem solving, and technology and problem solving.

Problem Solving as a Process

Garofola and Lester (10) have suggested that students are largely unaware of the processes involved in problem solving and that addressing this issue within problem solving instruction may be important. We will discuss various areas of research pertaining to the process of problem solving.

Domain Specific Knowledge

To become a good problem solver in mathematics, one must develop a base of mathematics knowledge. How effective one is in organizing that knowledge also contributes to successful problem solving. Kantowski (13) found that those students with a good knowledge base were most able to use the heuristics in geometry instruction. Schoenfeld and Herrmann (38) found that novices attended to surface features of problems whereas experts categorized problems on the basis of the fundamental principles involved. Silver (39) found that successful problem solvers were more likely to categorize math problems on the basis of their underlying similarities in mathematical structure. Wilson (50) found that general heuristics had utility only when preceded by task specific heuristics. The task specific heuristics were often specific to the problem domain, such as the tactic most students develop in working with trigonometric identities to "convert all expressions to functions of sine and cosine and do algebraic simplification."

Theories of mathematics problem solving (25,33,50) have placed a major focus on the role of heuristics. Surely it seems that providing explicit instruction on the development and use of heuristics should enhance problem solving performance; yet it is not that simple. Schoenfeld (35) and Lesh (19) have pointed out the limitations of such a simplistic analysis. Theories must be enlarged to incorporate classroom contexts, past knowledge and experience, and beliefs. What Polya (26) describes in How to Solve It is far more complex than any theories we have developed so far.

Mathematics instruction stressing heuristic processes has been the focus of several studies. Kantowski (14) used heuristic instruction to enhance the geometry problem solving performance of secondary school students. Wilson (50) and Smith (42) examined contrasts of general and task specific heuristics. These studies revealed that task specific hueristic instruction was more effective than general hueristic instruction. Jensen (12) used the heuristic of subgoal generation to enable students to form problem solving plans. He used thinking aloud, peer interaction, playing the role of teacher, and direct instruction to develop students' abilities to generate subgoals.

Managing It All

An extensive knowledge base of domain specific information, algorithms, and a repertoire of heuristics are not sufficient during problem solving. The student must also construct some decision mechanism to select from among the available heuristics, or to develop new ones, as problem situations are encountered. A major theme of Polya's writing was to do mathematics, to reflect on problems solved or attempted, and to think (27,28). Certainly Polya expected students to engage in thinking about the various tactics, patterns, techniques, and strategies available to them. To build a theory of problem solving that approaches Polya's model, a manager function must be incorporated into the system. Long ago, Dewey (8), in How We Think , emphasized self-reflection in the solving of problems.

Recent research has been much more explicit in attending to this aspect of problem solving and the learning of mathematics. The field of metacognition concerns thinking about one's own cognition. Metacognition theory holds that such thought can monitor, direct, and control one's cognitive processes (4,41). Schoenfeld (34) described and demonstrated an executive or monitor component to his problem solving theory. His problem solving courses included explicit attention to a set of guidelines for reflecting about the problem solving activities in which the students were engaged. Clearly, effective problem solving instruction must provide the students with an opportunity to reflect during problem solving activities in a systematic and constructive way.

The Importance of Looking Back

Looking back may be the most important part of problem solving. It is the set of activities that provides the primary opportunity for students to learn from the problem. The phase was identified by Polya (26) with admonitions to examine the solution by such activities as checking the result, checking the argument, deriving the result differently, using the result, or the method, for some other problem, reinterpreting the problem, interpreting the result, or stating a new problem to solve.

Teachers and researchers report, however, that developing the disposition to look back is very hard to accomplish with students. Kantowski (14) found little evidence among students of looking back even though the instruction had stressed it. Wilson (51) conducted a year long inservice mathematics problem solving course for secondary teachers in which each participant developed materials to implement some aspect of problem solving in their on-going teaching assignment. During the debriefing session at the final meeting, a teacher put it succinctly: "In schools, there is no looking back." The discussion underscored the agreement of all the participants that getting students to engage in looking back activities was difficult. Some of the reasons cited were entrenched beliefs that problem solving in mathematics is answer getting; pressure to cover a prescribed course syllabus; testing (or the absence of tests that measure processes); and student frustration.

The importance of looking back, however, outweighs these difficulties. Five activities essential to promote learning from problem solving are developing and exploring problem contexts, extending problems, extending solutions, extending processes, and developing self-reflection. Teachers can easily incorporate the use of writing in mathematics into the looking back phase of problem solving. It is what you learn after you have solved the problem that really counts.

Problem Posing

Problem solving as an instructional goal, what is mathematics.

If our answer to this question uses words like exploration, inquiry, discovery, plausible reasoning, or problem solving, then we are attending to the processes of mathematics. Most of us would also make a content list like algebra, geometry, number, probability, statistics, or calculus. Deep down, our answers to questions such as What is mathematics? What do mathematicians do? What do mathematics students do? Should the activities for mathematics students model what mathematicians do? can affect how we approach mathematics problems and how we teach mathematics.

The National Council of Teachers of Mathematics recommends that problem solving be the focus of school mathematics in the 1980s.         An Agenda for Action (23) We strongly endorse the first recommendation of An Agenda for Action. The initial standard of each of the three levels addresses this goal.          Curriculum and Evaluation Standards (24)

Why Problem Solving?

The NCTM (23,24) has strongly endorsed the inclusion of problem solving in school mathematics. There are many reasons for doing this. First, problem solving is a major part of mathematics. It is the sum and substance of our discipline and to reduce the discipline to a set of exercises and skills devoid of problem solving is misrepresenting mathematics as a discipline and shortchanging the students. Second, mathematics has many applications and often those applications represent important problems in mathematics. Our subject is used in the work, understanding, and communication within other disciplines. Third, there is an intrinsic motivation embedded in solving mathematics problems. We include problem solving in school mathematics because it can stimulate the interest and enthusiasm of the students. Fourth, problem solving can be fun. Many of us do mathematics problems for recreation. Finally, problem solving must be in the school mathematics curriculum to allow students to develop the art of problem solving. This art is so essential to understanding mathematics and appreciating mathematics that it must be an instructional goal.

Teachers often provide strong rationale for not including problem solving activities is school mathematics instruction. These include arguments that problem solving is too difficult, problem solving takes too much time, the school curriculum is very full and there is no room for problem solving, problem solving will not be measured and tested, mathematics is sequential and students must master facts, procedures, and algorithms, appropriate mathematics problems are not available, problem solving is not in the textbooks, and basic facts must be mastered through drill and practice before attempting the use of problem solving. We should note, however, that the student benefits from incorporating problem solving into the mathematics curriculum as discussed above outweigh this line of reasoning. Also we should caution against claiming an emphasize on problem solving when in fact the emphasis is on routine exercises. From various studies involving problem solving instruction, Suydam (44) concluded:

If problem solving is treated as "apply the procedure," then the students try to follow the rules in subsequent problems. If you teach problem solving as an approach, where you must think and can apply anything that works, then students are likely to be less rigid. (p. 104)

Problem Solving as an Instructional Method

Problem solving as a method of teaching may be used to accomplish the instructional goals of learning basic facts, concepts, and procedures, as well as goals for problem solving within problem contexts. For example, if students investigate the areas of all triangles having a fixed perimeter of 60 units, the problem solving activities should provide ample practice in computational skills and use of formulas and procedures, as well as opportunities for the conceptual development of the relationships between area and perimeter.   The "problem" might be to find the triangle with the most area, the areas of triangles with integer sides, or a triangle with area numerically equal to the perimeter. Thus problem solving as a method of teaching can be used to introduce concepts through lessons involving exploration and discovery. The creation of an algorithm, and its refinement, is also a complex problem solving task which can be accomplished through the problem approach to teaching. Open ended problem solving often uses problem contexts, where a sequence of related problems might be explored. For example, the problems in the investigations in the insert evolved from considering gardens of different shapes that could be enclosed with 100 yards of fencing:

Suppose one had 100 yards of fencing to enclose a garden. What shapes could be enclosed? What are the dimensions of each and what is the area? Make a chart. What triangular region with P = 100 has the most area? Find all five triangular regions with P = 100 having integer sides and integer area. (such as 29, 29, 42) What rectangular regions could be enclosed? Areas? Organize a table? Make a graph? Which rectangular region has the most area? from a table? from a graph? from algebra, using the arithmetic mean-geometric mean inequality? What is the area of a regular hexagon with P = 100? What is the area of a regular octagon with P = 100? What is the area of a regular n-gon with P = 100? Make a table for n = 3 to 25. Make a graph. What happens to 1/n(tan 180/n) as n increases? What if part of the fencing is used to build a partition perpendicular to a side? Consider a rectangular region with one partition? With 2 partitions? with n partitions? (There is a surprise in this one!!) What if the partition is a diagonal of the rectangle? What is the maximum area of a sector of a circle with P = 100? (Here is another surprise!!! -- could you believe it is r2 when r = 25? How is this similar to a square being the maximum rectangle and the central angle of the maximum sector being 2 radians?) What about regions built along a natural boundary? For example the maximum for both a rectangular region and a triangular region built along a natural boundary with 100 yards of fencing is 1250 sq. yds. But the rectangle is not the maximum area four-sided figure that can be built. What is the maximum-area four-sided figure?

Many teachers in our workshops have reported success with a "problem of the week" strategy. This is often associated with a bulletin board in which a challenge problem is presented on a regular basis (e.g., every Monday). The idea is to capitalize on intrinsic motivation and accomplishment, to use competition in a constructive way, and to extend the curriculum. Some teachers have used schemes for granting "extra credit" to successful students. The monthly calendar found in each issue of The Mathematics Teacher is an excellent source of problems.

Whether the students encounter good mathematics problems depends on the skill of the teacher to incorporate problems from various sources (often not in textbooks). We encourage teachers to begin building a resource book of problems oriented specifically to a course in their on-going workload. Good problems can be found in the Applications in Mathematics (AIM Project) materials (21) consisting of video tapes, resource books and computer diskettes published by the Mathematical Association of America. These problems can often be extended or modified by teachers and students to emphasize their interests. Problems of interest for teachers and their students can also be developed through the use of The Challenge of the Unknown materials (1) developed by the American Association for the Advancement of Science. These materials consist of tapes providing real situations from which mathematical problems arise and a handbook of ideas and activities that can be used to generate other problems.

Beliefs about Mathematics Problem Solving

Schoenfeld (36,37) reported results from a year-long study of detailed observations, analysis of videotaped instruction, and follow-up questionnaire data from two tenth-grade geometry classes. These classes were in select high schools and the classes were highly successful as determined by student performance on the New York State Regent's examination. Students reported beliefs that mathematics helps them to think clearly and they can be creative in mathematics, yet, they also claimed that mathematics is learned best by memorization. Similar contrasts have been reported for the National Assessment (5). Indeed our conversations with teachers and our observations portray an overwhelming predisposition of secondary school mathematics students to view problem solving as answer getting, view mathematics as a set of rules, and be highly oriented to doing well on tests. Schoenfeld (37) was able to tell us much more about the classes in his study. He makes the following points.

The rhetoric of problem solving has become familiar over the past decade. That rhetoric was frequently heard in the classes we observed -- but the reality of those classrooms is that real problems were few and far between . . . virtually all problems the students were asked to solve were bite-size exercises designed to achieve subject matter mastery: the exceptions were clearly peripheral tasks that the students found enjoyable but that they considered to be recreations or rewards rather than the substance they were expected to learn . . . the advances in mathematics education in the [past] decade . . . have been largely in our acquiring a more enlightened goal structure, and having students pick up the rhetoric -- but not the substance -- related to those goals. (pp. 359-9)

Each of us needs to ask if the situation Schoenfeld describes is similar to our own school. We must take care that espoused beliefs about problem solving are consistent with a legitimately implemented problem solving focus in school mathematics.

Technology and Problem Solving

The appropriate use of technology for many people has significant identity with mathematics problem solving. This view emphasizes the importance of technology as a tool for mathematics problem solving. This is in contrast to uses of technology to deliver instruction or for generating student feedback.

Programming as Problem Solving

In the past, problem solving research involving technology has often dealt with programming as a major focus. This research has often provided inconclusive results. Indeed, the development of a computer program to perform a mathematical task can be a challenging mathematical problem and can enhance the programmer's understanding of the mathematics being used. Too often, however, the focus is on programming skills rather than on using programming to solve mathematics problems. There is a place for programming within mathematics study, but the focus ought to be on the mathematics problems and the use of the computer as a tool for mathematics problem solving.

A ladder 5 meters long leans against a wall, reaching over the top of a box that is 1 meter on each side. The box is against the wall. What is the maximum height on the wall that the ladder can reach? The side view is: Assume the wall is perpendicular to the floor. Use your calculator to find the maximum height to the nearest .01 meter.

Iteration and recursion are concepts of mathematics made available to the secondary school level by technology. Students may implement iteration by writing a computer program, developing a procedure for using a calculator, writing a sequence of decision steps, or developing a classroom dramatization. The approximation of roots of equations can be made operational with a calculator or computer to carry out the iteration. For example, the process for finding the three roots of

is not very approachable without iterative techniques. Iteration is also useful when determining the maximum height, h , between a chord and an arc of a circle when the length S of the arc and the length L of the chord are known. This may call for solving

simultaneously and using iterative techniques to find the radius r and and central angle ø in order to evaluate h = r - r cos ø . Fractals can also be explored through the use of iterative techniques and computer software.

Exploration

Technology can be used to enhance or make possible exploration of conceptual or problem situations. For example, a function grapher computer program or a graphics calculator can allow student exploration of families of curves such as

for different values of a , b , and c . A calculator can be used to explore sequences such as

for different values of a . In this way, technology introduces a dynamic aspect to investigating mathematics. Thomas (46) studied the use of computer graphic problem solving activities to assist in the instruction of functions and transformational geometry at the secondary school level. The students were challenged to create a computer graphics design of a preselected picture using graphs of functions and transformational geometry. Thomas found these activities helped students to better understand function concepts and improved student attitudes.

Evaluation of Problem Solving

As the emphasis on problem solving in mathematics classrooms increases, the need for evaluation of progress and instruction in problem solving becomes more pressing. It no longer suffices for us to know which kinds of problems are correctly and incorrectly solved by students. As Schoenfeld (36) describes:

All too often we focus on a narrow collection of well-defined tasks and train students to execute those tasks in a routine, if not algorithmic fashion. Then we test the students on tasks that are very close to the ones they have been taught. If they succeed on those problems, we and they congratulate each other on the fact that they have learned some powerful mathematical techniques. In fact, they may be able to use such techniques mechanically while lacking some rudimentary thinking skills. To allow them, and ourselves, to believe that they "understand" the mathematics is deceptive and fraudulent. (p. 30)

Schoenfeld (31) indicates that capable mathematics students when removed from the context of coursework have difficulty doing what may be considered elementary mathematics for their level of achievement. For example, he describes a situation in which he gave a straightforward theorem from tenth grade plane geometry to a group of junior and senior mathematics majors at the University of California involved in a problem solving course. Of the eight students solving this problem only two made any significant progress. We need to focus on the teaching and learning of mathematics and, in turn, problem solving using a holistic approach. As recommended in the NCTM's An Agenda for Action (23), "the success of mathematics programs and student learning [must] be evaluated by a wider range of measures than conventional testing" (p. 1). Although this recommendation is widely accepted among mathematics educators, there is a limited amount of research dealing with the evaluation of problem solving within the classroom environment.

Classroom research : Ask your students to keep a problem solving notebook in which they record on a weekly basis: (1) their solution to a mathematics problem. (2) a discussion of the strategies they used to solve the problem. (3) a discussion of the mathematical similarities of this problem with other problems they have solved. (4) a discussion of possible extensions for the problem. (5) an investigation of at least one of the extensions they discussed.

Use these notebooks to evaluate students' progress. Then periodically throughout the year, analyze the students' overall progress as well as their reactions to the notebooks in order to asses the effectiveness of the evaluation process.

Some research dealing with the evaluation of problem solving involves diagnosing students' cognitive processes by evaluating the amount and type of help needed by an individual during a problem solving activity. Campione, Brown, and Connell (4) term this method of evaluation as dynamic assessment. Students are given mathematics problems to solve. The assessor then begins to provide as little help as necessary to the students throughout their problem solving activity. The amount and type of help needed can provide good insight into the students' problem solving abilities, as well as their ability to learn and apply new principles. Trismen (47) reported the use of hints to diagnosis student difficulties in problem solving in high school algebra and plane geometry. Problems were developed such that the methods of solutions where not readily apparent to the students. A sequence of hints was then developed for each item. According to Trismen, "the power of the hint technique seems to lie in its ability to identify those particular students in need of special kinds of help" (p. 371).

Campione and his colleagues (4) also discussed a method to help monitor and evaluate the progress of a small cooperative group during a problem solving session. A learning leader (sometimes the teacher sometimes a student) guides the group in solving the problem through the use of three boards: (1) a Planning Board, where important information and ideas about the problem are recorded, (2) a Representation Board, where diagrams illustrating the problems are drawn, and (3) a Doing Board, where appropriate equations are developed and the problem is solved. Through the use of this method, the students are able to discuss and reflect on their approaches by visually tracing their joint work. Campione and his colleagues indicated that increased student engagement and enthusiasm in problem solving, as well as, increased performance resulted from the use of this method for solving problems.

Methods, such as the clinical approach discussed earlier, used to gather data dealing with problem solving and individual's thinking processes may also be used in the classroom to evaluate progress in problem solving. Charles, Lester, and O'Daffer (7) describe how we may incorporate these techniques into a classroom problem solving evaluation program. For example, thinking aloud may be canonically achieved within the classroom by placing the students in cooperative groups. In this way, students may express their problem solving strategies aloud and thus we may be able to assess their thinking processes and attitudes unobtrusively. Charles and his colleagues also discussed the use of interviews and student self reports during which students are asked to reflect on their problem solving experience a technique often used in problem solving research. Other techniques which they describe involve methods of scoring students' written work. Figure 3 illustrates a final assignment used to assess teachers' learning in a problem solving course that has been modified to be used with students at the secondary level.

Testing, unfortunately, often drives the mathematics curriculum. Most criterion referenced testing and most norm referenced testing is antithetical to problem solving. Such testing emphasizes answer getting. It leads to pressure to "cover" lots of material and teachers feel pressured to forego problem solving. They may know that problem solving is desirable and developing understanding and using appropriate technology are worthwhile, but ... there is not enough time for all of that and getting ready for the tests. However, teachers dedicated to problem solving have been able to incorporate problem solving into their mathematics curriculum without bringing down students' scores on standardized tests. Although test developers, such as the designers of the California Assessment Program, are beginning to consider alternative test questions, it will take time for these changes to occur. By committing ourselves to problem solving within our classrooms, we will further accentuate the need for changes in testing practices while providing our students with invaluable mathematics experiences.

Looking Ahead ...

The primary goal of most students in mathematics classes is to see an algorithm that will give them the answer quickly. Students and parents struggle with (and at times against) the idea that math class can and should involve exploration, conjecturing, and thinking. When students struggle with a problem, parents often accuse them of not paying attention in class; "surely the teacher showed you how to work the problem!" How can parents, students, colleagues, and the public become more informed regarding genuine problem solving? How can I as a mathematics teacher in the secondary school help students and their parents understand what real mathematics learning is all about?

*1. American Association for the Advancement of Science. (1986). The challenge of the unknown. New York: Norton. 2. Bobrow, D. G. (1964). Natural language input for a computer problem solving system. Unpublished doctoral dissertation, Massachusetts Institute of Technology, Boston. *3. Brown, S. I. & Walter, M. I. (1983). The art of problem posing. Hillsdale, NJ: Lawrence Erlbaum. *4. Campione, J. C., Brown, A. L., & Connell, M. L. (1988). Metacognition: On the importance of understanding what you are doing. In R. I. Charles & E. A. Silver (Eds.), The teaching and assessing of mathematical problem solving (pp. 93-114). Reston, VA: Lawrence Erlbaum, National Council of Teachers of Mathematics. 5. Carpenter, T. P., Lindquist, M. M., Matthews, W., & Silver, E. A. (1983). Results of the third NAEP mathematics assessment: Secondary school. Mathematics Teacher, 76 (9), 652-659. 6. Carpenter, T. P., Moser, J. M., & Romberg, T. A. (Eds.) (1982). Addition and subtraction: A cognitive perspective. Hillsdale, NJ: Lawrence Erlbaum. *7. Charles, R. I., Lester, F. K., & O'Daffer, P. (1987). How to evaluate progress in problem solving. Reston, VA: National Council of Teachers of Mathematics. 8. Dewey, J. (1933). How we think: A restatement of the relation of reflective thinking to the educative process. Boston: Heath. 9. Frederiksen, N. (1984). Implications of cognitive theory for instruction in problem solving. Review of Educational Research, 54, 363-407. 10. Garfola, J. & Lester, F. K. (1985). Metacognition, cognitive monitoring, and mathematical performance. Journal for Research in Mathematics Education, 16, 163-176. 11. Henderson, K. B. & Pingry, R. E. (1953). Problem solving in mathematics. In H. F. Fehr (Ed.), The learning of mathematics: Its theory and practice (21st Yearbook of the National Council of Teachers of Mathematics) (pp. 228-270). Washington, DC: National Council of Teachers of Mathematics. 12. Jensen, R. (1984). A multifaceted instructional approach for developing subgoal generation skills. Unpublished doctoral dissertation, The University of Georgia. 13. Kantowski, M. G. (1974). Processes involved in mathematical problem solving. Unpublished doctoral dissertation, The University of Georgia, Athens. 14. Kantowski, M. G. (1977). Processes involved in mathematical problem solving. Journal for Research in Mathematics Education, 8, 163-180. 15. Kaput, J. J. (1979). Mathematics learning: Roots of epistemological status. In J. Lochhead and J. Clement (Eds.), Cognitive process instruction. Philadelphia, PA: Franklin Institute Press. 16. Kilpatrick, J. (1987). Problem formulating: Where do good problems come from? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123-147). Hillsdale, NJ: Lawrence Erlbaum. 17. Kulm, G. (Ed.) (1990). Assessing higher order thinking skills. Washington, D.C.: American Association for the Advancement of Science. 18. Larkin, J. (1980). Teaching problem solving in physics: The psychological laboratory and the practical classroom. In F. Reif & D. Tuma (Eds.), Problem solving in education: Issues in teaching and research. Hillsdale, NJ: Lawrence Erlbaum. 19. Lesh, R. (1981). Applied mathematical problem solving. Educational Studies in Mathematics, 12(2), 235-265. 20. Lochhead, J. (1979). An introduction to cognitive process instruction. In J. Lochhead and J. Clement (Eds.). Cognitive process instruction. Philadelphia, PA: Franklin Institute Press. *21. Mathematical Association of America. (1986). Applications in mathematics (AIM Project materials). Washington, DC: The Author. 22. National Council of Supervisors of Mathematics. (1978). Position paper on basic mathematical skills. Mathematics Teacher, 71(2), 147-52. (Reprinted from position paper distributed to members January 1977.) 23. National Council of Teachers of Mathematics. (1980). An agenda for action: Recommendations for school mathematics in the 1980s. Reston, VA: The Author. 24. National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: The Author. 25. Newell, A. & Simon, H. A. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice Hall. *26. Polya, G. (1973). How to solve it. Princeton, NJ: Princeton University Press. (Originally copyrighted in 1945). 27. Polya, G. (1962). Mathematical discovery: On understanding, learning and teaching problem solving (vol. 1). New York: Wiley. 28. Polya, G. (1965). Mathematical discovery: On understanding, learning and teaching problem solving (vol. 2). New York: Wiley. 29. Reitman, W. R. (1965). Cognition and thought. New York: Wiley. 30. Riley, M.S., Greeno, J. G., & Heller, J. I. (1983). Development of children's problem-solving ability in arithmetic. In H. Ginsburg (Ed.), The development of mathematical thinking (pp. 153-200). New York: Academic Press. 31. Schoenfeld, A. H. (1979). Can heuristics be taught? In J. Lockhead, Cognitive process instruction. Philadelphia, PA: Franklin Institute Press. 32. Schoenfeld, A. H. (1983). Episodes and executive decisions in mathematics problem solving. In R. Lesh & M. Landau, Acquisition of mathematics concepts and processes. New York: Academic Press 33. Schoenfeld, A. H. (1985). Mathematical problem solving. Orlando, FL: Academic Press. 34. Schoenfeld, A. H., (1985). Metacognitive and epistemological issues in mathematical understanding. In E. A. Silver, Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 361-379). Hillsdale, NJ: Lawrence Erlbaum. 35. Schoenfeld, A. H. (1987). Cognitive science and mathematics education: An overview. In A. H. Schoenfeld, Cognitive science and mathematics education. Hillsdale, NJ: Lawrence Erlbaum. 36. Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of "well taught" mathematics classes. Educational Psychologist, 23, 145-166. 37. Schoenfeld, A. H. (1989). Explorations of students' mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20, 338-355. 38. Schoenfeld, A. H., & Herrmann, D. (1982). Problem perception and knowledge structure in expert and novice mathematical problem solvers. Journal of Experimental Psychology: Learning, Memory and Cognition, 8, 484-494. 39. Silver, E. A. (1979). Student perceptions of relatedness among mathematical verbal problems. Journal for Research in Mathematics Education, 10(3), 195-210. 40. Silver, E. A. (1987). Foundations of cognitive theory and research for mathematics problem-solving instruction. In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 33-60). Hillsdale, NJ: Lawrence Erlbaum. 41. Silver, E. A., Branca, N., & Adams, V. (1980). Metacognition: The missing link in problem solving? In R. Karplus, (Ed.), Proceedings of the fourth international conference for the psychology of mathematics education. Berkeley, CA: PME. 42. Smith, J. P. (1974). The effects of general versus specific heuristics in mathematical problem-solving tasks (Columbia University, 1973). Dissertation Abstracts International, 34, 2400A. 43. Stanic, G., & Kilpatrick, J. (1988). Historical Perspectives on Problem Solving in the Mathematics Curriculum. In R. I. Charles & E. A. Silver (Eds.), The teaching and assessing of mathematical problem solving (pp. 1-22). Reston, VA: National Council of Teachers of Mathematics. 44. Suydam, M. (1987). Indications from research on problem solving. In F. R. Curcio (Ed.), Teaching and learning: A problem solving focus. Reston, VA: National Council of Teachers of Mathematics. 45. Steffe, L. P., & Wood, T. (Eds.). (1990). Transforming Children's Mathematical Education. Hillsdale, NJ: Lawrence Erlbaum. 46. Thomas, E. J. Jr. (1990). A study of the effects of a computer graphics problem-solving activity on student achievements, attitudes, and task motivation. (Georgia State University, 1989). Dissertation Abstracts International, 51, 102A. 47. Trismen, D. A. (1988). Hints: An aid to diagnosis in mathematical problem solving. Journal for Research in Mathematics Education, 19, 358-361. 48. von Glasersfeld, E. (1989). Constructivism in education. In T. Husen & T. N. Postlethwaite (Eds.), The international encyclopedia of education. (pp. 162-163). (Suppl. Vol. I). New York: Pergammon. 49. Waters, W. (1984). Concept acquisition tasks. In G. A. Goldin & C. E. McClintock (Eds.), Task variables in mathematical problem solving (pp. 277-296). Philadelphia, PA: Franklin Institute Press. 50. Wilson, J. W. (1967). Generality of heuristics as an instructional variable. Unpublished Doctoral Dissertation, Stanford University, San Jose, CA. 51. Wilson, J. W. (1990) Report of the Georgia Plan problem solving workshop, 1989-90. Unpublished document, The University of Georgia, Athens.

Wilson, P. S. (Ed.)(1993). Research Ideas for the Classroom: High School Mathematics. New York: MacMillan.

The book was part of the National Council of Teacher of Mathematics Research Interpretation Project, directed by Sigrid Wagner.

Nelda Hadaway received a B.S. Ed., an M. Ed., and an Ed. S. from The University of Georgia in Athens, Georgia and the Ph. D. from Georgia State University in Atlanta. She has taught mathematics at Hunter College High School in the New YorkCity and is retired from mathematics teaching at South Gwinnett High School in Snellville, Georgia. She is interested in integrating writing into the teaching of mathematics to enhance problem solving.  She is currently a part time Assistant Professor of Mathematics at Kennesaw State University. James W. Wilson is a retired Professor of Mathematics Education at The University of Georgia. He has a B.S. and M.A. from Kansas State Teachers College, M.S. from University of Notre Dame, and M.S. and Ph.D. from Stanford University. He has been interested in problem solving for many years. His doctoral research dealt with problem solving and his Problem Solving in Mathematics course is a regular offering at The University of Georgia. Over the years, he has also been involved in various problem solving projects including the U.S.-Japan Joint Seminar on Problem Solving in School Mathematics.  He retired in 2015. Maria L. Fernandez is an Associate Professor of Mathematics Education at Florida International University.  She completed both a B.S. and M.S. in Mathematics Education at Florida International University in Miami, Florida and the Ph. D. at the University of Georgia. She previously taught at the University of Arizona and at Florida State University.   She is interested in incorporating problem solving into the mathematics curriculum at all levels. While teaching mathematics at the secondary level in Miami, she integrated problem solving into the curriculum using various strategies. Her research interests involve mathematics visualizations in problem solving.

Towards the modelling of mathematical metacognition

• Published: June 2004
• Volume 16 , pages 25–48, ( 2004 )

Cite this article

• Jeni Wilson 1 &
• David Clarke 2  

1323 Accesses

61 Citations

Explore all metrics

Metacognition has been accorded a role in both mathematical problem solving and in the learning of mathematics. There has been consistent advocacy of the need for the promotion of metacognitive activity in both domains. Such advocacy can only be effective if the advocated process is well understood. In this paper we have four goals: to describe a multi-method technique developed to study student mathematical metacognition; to set out the structural elements and configuration of a coherent model of metacognition in the domain of mathematical problem solving; to report on the empirical utility (and validity) of this model; and, to report the insights into student mathematical metacognition arising from the research.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

The use of cronbach’s alpha when developing and reporting research instruments in science education, effects of a rubric for mathematical reasoning on teaching and learning in primary school.

The Value of Using Tests in Education as Tools for Learning—Not Just for Assessment

Artzt, A., & Armour-Thomas, E. (1992). Development of a cognitive-metacognitive framework for protocol analysis of mathematical problem solving in small groups. Cognition and Instruction, 9 (2), 137–175.

Article   Google Scholar  

Baird, J. (1998). Promoting willingness and ability to learn: A focus on ignorance. The Journal of Reflection in Learning and Teaching, 4 (1), 21–26.

Google Scholar  

Baird, J. (2001). Learning and teaching: From ignorance to understanding. In D. Clarke (Ed.), Perspectives on practice and meaning in mathematics and science classrooms (pp. 255–290). Dordrecht: Kluwer.

Baird, J. (2002). Volitional control and learning: A focus on “homework” . Paper presented at the American Education Research Association, New Orleans.

Baird, J., & Mitchell, I. (Eds.). (1986). Improving the quality of teaching and learning: An Australian case study — The PEEL Project . Melbourne: Monash University.

Baird, J., & Northfield, J. (Eds.). (1992). Learning from the PEEL experience . Melbourne: Monash University.

Biggs, J. (1987). The process of learning . Sydney: Prentice Hall.

Birenbaum, M. (1996). Assessment 2000: Towards a pluralistic approach to assessment. In M. Birenbaum & F. Dochy, (Eds.), Alternatives in assessment of achievements, learning processes and prior knowledge (pp. 3–30). Boston: Kluwer.

Borkowski, J., & Muthukrishna, N. (1992). Moving metacognition into the classroom: Working models and effective strategy teaching. In M. Pressley, K. Harris, & J. Guthrie (Eds.), Promoting competence and literacy in school (pp. 477–501). San Diego: Academic Press Inc.

Brown, A. (1987). Metacognition, executive control, self regulation and mysterious mechanisms. In F. Weinert & R. Klume (Eds.), Metacognition, motivation and understanding (pp. 65–117). Hillsdale, NJ: Erlbaum.

Brown, A., & De Loache, J. (1983). Metacognitive skills. In M. Donaldson, R. Grieve, & C. Pratt (Eds.), Early childhood development and education (pp. 3–35). Oxford: Blackwell.

Cardelle-Elawar, M. (1992). Effects of teaching metacognitive skills to students with low mathematical ability. Teaching and Teacher Education, 8 (2) 109–121.

Cavanaugh, J., & Perlmutter, M. (1982). Metamemory: A critical examination. Child Development, 53 , 11–28.

Clarke, D. (1989). The impact of the transition from primary to secondary schooling on student mathematics behaviour . Unpublished PhD thesis, Monash University, VIC.

Corno, L. (1993). The best laid plans, modern conceptions of volition and educational Research. Educational Researcher, 22 (2) 14–21.

Dunlosky, J. (1998). Epilogue: Linking metacognitive theory to education. In D. Hacker, J. Dunlosky, & A. Graesser (Eds.), Metacognition in educational theory and practice (pp. 367–381). Mahwah, NJ: Lawrence Erlbaum.

Ericsson, K., & Simon, H. (1980). Verbal reports as data. Psychological Review, 87 (3), 215–251.

Flavell, J. (1976). Metacognitive aspects of problem solving. In L. Resnick, (Ed.), The nature of intelligence (pp. 231–235). Hillsdale, NJ: Erlbaum.

Garofalo, J. (1989). Beliefs and their influence on mathematical performance. Mathematics Teacher, 82 , 502–505.

Garofalo, J., & Lester, F. (1985). Metacognition, cognitive monitoring and mathematical performance. Journal for Research in Mathematics Education, 16 (3), 163–176.

Goos, M. (1994). Metacognitive decision making and social interactions during paired problem solving. Mathematics Education Research Journal. 6 (2) 144–165.

Goos, M., & Galbraith, P. (1996). Do it this way! Metacognitive strategies in collaborative mathematical problem solving. Educational Studies in Mathematics, 30 , 229–260.

Haynes, F. (1997). Teaching to think. The Australian Journal of Teacher Education, 22 (1), 1–12.

Hacker, D., Dunlosky, J. & Graesser, A. (Eds.). (1998). Metacognition in educational theory and practice . Mahwah, NJ: Lawrence Erlbaum.

Hirabayashi, I., & Shigematsu, K. (1987). Metacognition: The role of the inner teacher. In J. C. Bergeron, N. Herscovics, & C. Kieran (Eds,), Proceedings of the Eleventh Annual Conference of the International Group for the Psychology of Mathematics Education (Vol.2, pp. 243–249). Montreal: University of Montreal.

Holton, D., & Clarke, D. (2002). Scaffolding and metacognition. Paper presented at the Annual Conference of the American Education Research Association , New Orleans, USA.

Holton, D., & Thomas, G. (2001). Mathematical interactions and their influence on learning. In D. Clarke (Ed.), Perspectives on practice and meaning in mathematics and science classrooms (pp. 75–104). Dordrecht, The Netherlands: Kluwer.

Kilpatrick, J. (1985). Reflection and recursion. Educational Studies in Mathematics, 16 , 1–26.

Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren . Chicago: University of Chicago Press.

Lester, F., Garofalo, J., & Kroll, L. (1989). Self confidence, interest, beliefs and metacognition: Key influences on problem solving behavior. In D. B. McLeod & V. M. Adams (Eds.), Affect and mathematical problem solving: A new perspective (pp. 75–88). New York: Springer-Verlag.

McKoon, G., & Ratcliff, R. (1992). Inference during reading. Psychological Review, 99 , 440–466.

Meichenbaum, D., Burland, B., Gruson, L., & Cameron, R. (1985). Metacognitive assessment. In S. Yussen (Ed.), The growth of reflection in children (pp. 3–30). London: Academic Press.

Mulcahy, R., Short, R., & Andrews, J. (Eds.). (1991). Enhancing learning and thinking . New York: Praeger.

Nelson, T., Kruglanski, A., & Jost, J. (1998). Knowing thyself and others: Progress in metacognitive social psychology. In V. Yzerbyt, G. Lories, & B. Dardenne (Eds.), Metacognition: Cognitive and social dimensions (pp. 69–89). London: Sage.

Newfield, J. (1980). Accuracy of teacher reports of specific classroom behaviors. Journal of Educational Research, 74 , 78–82.

Nisbett, R., & Wilson, T. (1977). Telling more than we can know: Verbal reports on mental processes. Psychological Review, 84 , 231–259.

Randhawa, B. (1994). Theory, research, and assessment of mathematical problem solving. The Alberta Journal of Educational Research, XL (2), 213–231.

Schoenfeld, A. (1987). What’s all the fuss about metacognition? In A. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 334–370). Hillsdale, NJ: Erlbaum.

Schoenfeld, A. (1992). Learning to think mathematically: Problem solving, metacognition and sense making in mathematics. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 189–215). New York: Macmillan.

Silver, E. (1985). The teaching and assessing of mathematical problem solving . Reston, VA: National Council of Teachers of Mathematics [NCTM].

Stacey, K. (1991). Making optimal use of mathematical knowledge. Australian Journal of Remedial Education, 22 (4) 6–10.

Steffe, L. (2002). Written discussant’s comments on the papers presented in the AREA Symposium, Approaches to the study and promotion of learner self-control of learning . Presented at the Annual Conference of the American Education Research Association, New Orleans, USA.

Wilson, J. (2001). Assessing metacognition . Unpublished doctoral thesis, The University of Melbourne.

Wilson, J., & Wing Jan, L. (1993). Thinking for themselves . Melbourne: Eleanor Curtain.

Wilson, J., & Wing Jan, L. (1998). Self-assessment of students . Melbourne: Eleanor Curtain.

Wittrock, M. (Ed). (1986). Handbook of research on teaching (3rd ed). New York: Macmillan.

Download references

Author information

Authors and affiliations.

Faculty of Education, The University of Melbourne, 3010, Victoria

Jeni Wilson

International Centre for Classroom Research, Department of Science and Mathematics Education, Faculty of Education, University of Melbourne, 3010, Victoria

David Clarke ( Director )

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

About this article

Wilson, J., Clarke, D. Towards the modelling of mathematical metacognition. Math Ed Res J 16 , 25–48 (2004). https://doi.org/10.1007/BF03217394

Download citation

Issue Date : June 2004

DOI : https://doi.org/10.1007/BF03217394

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Cognitive Activity
• Thought Process
• Verbal Report
• Mathematical Ability
• Metacognitive Skill
• Find a journal
• Publish with us
• Track your research

Metacognition through prompts in mathematical problem-solving

• Original Research
• Published on: February 22, 2018

• Developing effective learners |
• Metacognition |
• Promoting good progress

Why problem-solving? Problem-solving has long had a strong emphasis in mathematics education. In 1982, the Cockcroft Report asserted that ‘the ability to solve problems is at the heart of mathematics’ (Cockcroft, 1982) . In recent years, as a result of reforms to the mathematics GCSE, a focus on problemsolving has re-emerged. A minimum of 30% of the marks in higher-tier GCSE papers now involve problem-solving (previously 15–25%), and students are increasingly required to make links between different areas of maths within a broad range of contexts (OFQUAL, 2015) .

As a consequence of these curriculum changes and exam reforms, it became apparent that many of my top set Year 11 students, who previously viewed themselves as strong mathematicians, were losing confidence in their ability to solve the increasingly difficult problems expected of them. In search of a possible solution to this, I developed and trialled a new approach to developing my students’ problem-solving abilities. Metacognition, which Swanson defines as ‘the knowledge and control one has over one’s thinking and learning activities’ ( (Swanson, 1990) , p. 306), formed the starting point for my research, because the ability to self-regulate one’s thoughts is both a common trait of expert problem-solvers (Swanson, 1990) and prominent in the EEF’s Teaching & Learning Toolkit (Education Endowment Foundation, 2017) . This then led me to the problem-solving heuristic developed by Polya (Polya, 1945) . Below, I note some of the key features of this heuristic before describing how I adapted it to use with my students.

Polya’s problem-solving heuristic

Heuristics, in the context of problemsolving, are a set of practical strategies to help students solve mathematical problems. Schoenfeld ( (Schoenfeld, 1987) , p. 284) aptly refers to heuristics as ‘rules of thumb for making progress on difficult problems’. Polya’s heuristic breaks problem-solving down into four stages for students to focus on:

• Stage 1: Understanding the problem
• Stage 2: Devising a plan
• Stage 3: Carrying out the plan
• Stage 4:  Looking back.

Students do not follow a linear path through these stages when working on a mathematical problem; instead, they tend to alternate between stages (Liljedahl, 2016) . For example, a failed attempt to carry out a plan (Stage 3) may lead students to devise a new plan (Stage 2) or prompt a realisation that they may not have fully understood the problem, which would lead them back to Stage 1.

Within each of the stages, a number of prompts are provided to help students move towards a solution to their problem. For example, Stage 1 includes prompts such as ‘what is the unknown?’ and ‘draw a figure’. The intention of these prompts is not to forge a definite path towards the solution, but to provide potential avenues of thought that could be productive when students are stuck. Not every prompt is useful in every situation but, together, they provide the problem-solver with a toolkit to aid the solution of a variety of problems (Polya, 1945) .

Polya’s heuristic has been shown to improve students’ self-confidence in answering problem-solving questions (Schoenfeld, 1987) . However, researchers have cautioned against encouraging learners to follow the heuristic too rigidly; doing so can impede attempts to solve problems using their natural powers (Bruder, 2016) . Liljedahl (Liljedahl, 2016) has also noted that the utility of the prompts relies heavily on the past experiences and mathematical content knowledge of the problem-solver. Therefore, use of the prompts themselves is not enough: it is important that students are regularly given mathematical problems to solve throughout their school career so that they can build a repertoire of experiences that they can link to future problems.

Adapted problem-solving prompts

In light of the criticisms highlighted above, I wanted to adapt Polya’s heuristic and develop my own set of prompts to support students. The intention was to move the emphasis away from practical problem-solving strategies (e.g. ‘draw a figure’ or ‘can you specialise/ generalise?’) and instead focus on encouraging metacognitive thinking in order to initiate deeper thinking about the problems themselves and their links to prior knowledge (Schoenfeld, 1987) . Kramarski et al. ( (Kramarski et al., 2002) , p. 228) highlight the four main areas in which students can be trained to use metacognitive thinking to aid problem-solving:

a) Comprehending the problem

b) Constructing connections between previous and new knowledge

c) Using strategies appropriate for solving the problem

d) Reflecting on the processes and the solution.

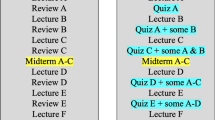
Clearly, there are strong parallels between these four areas and the four stages of Polya’s problem-solving heuristic. The set of prompts that I generated evolved over the course of several months as a direct result of feedback from students. The final set of prompts are displayed in Figure 1.

Implementation in the classroom

The prompts were first introduced to students in conjunction with a difficult maths problem. Students were given time to work on the problem independently before being asked to explicitly answer the prompt questions. The aim was to get them thinking metacognitively about what the problem was asking them to do, and how it related to their mathematical content knowledge and previous problems they had worked on. Students then went back to answering the problem, with many now finding a path towards the solution. This is in keeping with the research literature, which suggests that problem-solving prompts can help students make progress with difficult problems (Bruder, 2016) .

In the lessons that followed, I modelled use of the prompts to solve a variety of problems until the class became more familiar with them. Research suggests that explicit modelling by the teacher and opportunities to reflect on problemsolving strategies are crucial for the development of both problem-solving abilities and metacognitive thinking (Bruder, 2016) . In later lessons, students were encouraged to share, through class discussion, where and how they had used the prompts in order to support the answering of problems. These class discussions were crucial because cooperative settings where students are encouraged to elaborate on their mathematical reasoning and reflect on their learning are integral for embedding metacognitive strategies (Kramarski et al., 2002) .

Classroom impact

After two lessons, the 30 students in my class were given a survey. Students were asked questions such as: ‘Which prompt do you find least/most useful and why?’ and ‘How useful do you think these prompts are for helping you to answer problem-solving questions?’. Ninety per cent of students said that they had found at least one of the prompts useful in solving the problems and, interestingly, there was a great deal of variety in the prompts that students favoured. I was careful to emphasise this to the class and to highlight the fact that not all the prompts would be useful for every situation.

Over the following months, it became clear that students had begun to internalise the prompts and were using them metacognitively to help themselves make progress with problem-solving questions. Evidence of this could be inferred from their mock exam papers, where students explicitly listed out different areas of maths and key formulae that they thought could be relevant for particular questions (a reference to the prompt: ‘What areas of maths are involved?’). Further evidence could be inferred where students had begun to underline both key information given in questions (‘What information are you given to start with?’) and the unknown (‘What are you asked to find or show?’). Finally, there were examples, during group work, of students explicitly asking each other variations of the prompts as they worked on mathematical problems.

After several months, students were given the original survey and were asked to reflect again on the utility of the prompts. All students were able to articulate an aspect of the prompts that they believed had made them more successful problemsolvers. This was backed up by students’ mock exam papers, which showed a marked improvement in their facility with problem-solving questions over several months.

Conclusion and moving forward

Whilst the success of my students cannot be entirely attributed to the prompts (the increased focus on problem-solving in lessons surely helped), there is no doubt that the prompts provided a confidence boost to students as well as a structured way to model metacognitive thought processes. Evidence that students were engaging in metacognitive thought was explicit in their behaviour in the classroom and their survey responses, and also implicit in their responses to problemsolving questions in mock exams.

In order to maximise their impact, research suggests that such prompts should be introduced to students as early as possible and promoted regularly over a long period of time (Bruder, 2016) . As a department, we are now looking at how we can effectively expand the use of these prompts to support a wider range of year and ability groups. Our hope is that, by encouraging metacognition across the school, we can make students better problem-solvers and learners.

From this issue

Issue 3: Developing Effective Learners

Summer 2018

Impact Articles on the same themes

Effective leadership practices and teacher wellbeing: A review of international evidence

• Perspective Article

Can a collaborative approach to curriculum development aid teacher retention?

Collaborative CPD as a means to improve teacher expertise and retention

Reframing ‘disadvantaged’ as ‘underserved’ in mathematics education professional development design

Promoting effective teacher reflection through collaboration

Could the development of teacher self-efficacy enhance teachers’ own mental health and wellbeing?

Effective professional development at scale

Subject communities: Grow, nurture, sustain

• Teacher Reflection

Building a strong foundation: A new head of department’s perspective on professional development for a diverse team of PSHE Educators

‘Being’ a teacher – the impact of teacher identity on self-efficacy and professional development across a career

Pears Pavillion Corum Campus 41 Brunswick Square London WC1N 1AZ

[email protected] 020 3433 7624

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Table of Contents

Last modified on April 26th, 2024

#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline

Wilson’s theorem.

Wilson’s theorem states that any positive integer, n (> 1), is a prime number if and only if (n – 1)! ≡ -1 (mod n), which means:

• If (n – 1)! ≡ -1 (mod n), then n is prime
• If n is prime, then (n – 1)! ≡ -1 (mod n), the converse

It is used in mathematical calculations in elementary number theory involving (n – 1)!. Wilson’s theorem is also used in fields like cryptography for coding-decoding.

Proving: If (n – 1)! ≡ -1 (mod n), then n is prime

If possible, let ‘n’ be a composite number.

Since composite numbers have more than two factors, ‘n’ can be expressed as n = n 1 ⋅ n 2 where 1 < n 1 n 2 < n

Now, (n – 1)! = (n – 1)(n – 2)(n – 3)…3 ⋅ 2 ⋅ 1

Also, n 1 n 2 < n ⇒ n 1 n 2 ≤ (n – 1)

Thus, 1 < n 1 n 2 ≤ (n – 1)

Now, n 1 and n 2 are any two of the factors of (n – 1)! which is divisible by n 1 n 2

Thus, (n – 1)! ≡ 0 (mod n 1 n 2 ). 

Since n = n 1 n 2 , (n – 1)! ≡ 0 (mod n)……………..(i)

Given that (n – 1)! ≡ -1 (mod n)………….(ii)

This implies 0 ≡ -1 (mod n)

⇒ 0 + 1 ≡ 0 (mod n)

⇒ 1 ≡ 0 (mod n) means if we divide 1 by ‘n,’ the remainder will be 0.

⇒ n|1, which contradicts as ‘n’ is a composite number (by our assumption), and 1 can not be divisible by any composite number. 

Also, n 1 n 2 > 1 is another reason n = n 1 n 2 can not divide 1.

Thus, our assumption is wrong.

‘n’ must be a prime number.

Hence, it is proven.

Proving: If n is prime, then (n – 1)! ≡ -1 (mod n), the Converse

The converse of Wilson’s theorem can be proved in two ways.

1. Elementary Proof

Let ‘n’ be a prime number.

For the smallest prime number, n = 2: 1! ≡ -1 (mod 2). 

If n > 2, then for any a Є [1, n – 1], there exists b Є [1, n – 1], such that ab ≡ 1 (mod n)

Each integer a Є {1, …, n – 1} has an inverse in modulo n. 

This inverse is unique and denoted by a −1 (mod n). 

If a ≡ a −1 (mod n), a 2 – 1 ≡ 0 (mod n) 

⇒ (a − 1)(a + 1) ≡ 0 (mod n), which has two roots in modulo n: a ≡ 1 (mod n) and a ≡ -1 (mod n) 

⇒ a = 1 or a = n – 1

We can arrange all the integers 1, 2, …, n – 1, except for 1 and n – 1, into pairs {a, b}, such that ab ≡ 1 (mod n) except for 1 and n – 1 whose product is -1 (mod n).

Thus, (n – 1)! ≡ 1 ⋅ (n – 1) ≡ -1 (mod n).

2. Algebraic Proof

Considering the field of integers in modulo n, by Fermat’s little theorem, we know: 

Every non-zero element of this field is a root of the polynomial f(x) = x n – 1 – 1.

Since the field has only n – 1 non-zero elements, which follows that ${x^{n-1}-1=\prod ^{n-1}_{r=1}\left( x-r\right)}$

Now, either n = 2 or n – 1 is even.

For n = 2, a ≡ -a (mod 2) for any integer a,

For n – 1, (-1) n – 1 ≡ 1 (mod n) 

Thus, x^{n-1}-1=\prod ^{n-1}_{r=1}\left( x-r\right) =\prod ^{n-1}_{r=1}\left( -x+r\right)

By putting x = 0, we get (n – 1)! ≡ -1 (mod n)

Solved Examples

Evaluate 12! (mod 13)

As we know, by Wilson’s theorem, if n is a prime, then (n – 1)! ≡ -1 (mod n) Here, n = 13 is a prime Thus, 12! ≡ (13 – 1)! ≡ -1 (mod 13)

Show that if n is prime, (n – 2)! ≡ 1 (mod n)

As we know, by Wilson’s theorem, if n is a prime, then (n – 1)! ≡ -1 (mod n) (n – 1)! ≡ -1 ≡ (n – 1) (mod n) On dividing by n – 1 (≠ 0), we get (n – 2)! ≡ 1 (mod n) Thus, if n is a prime, (n – 2)! ≡ 1 (mod n)

Find the remainder when 171! is divided by 173.

As we know, by Wilson’s theorem, if n is a prime, then (n – 1)! ≡ -1 (mod n) ⇒ (n – 2)! ≡ 1 (mod n) Here, n = 173 is a prime Thus, 171! ≡ (173 – 2)! ≡ 1 (mod 173)

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Privacy Settings

You are welcome to change your privacy preferences here.

DEPARTMENTS

Mathematics.

AT WILSON’S SCHOOL

THE MATHEMATICS DEPARTMENT at Wilson’s is thriving and exceptionally successful. All pupils are fully engaged and stretched by high quality enrichment material which goes well beyond exam board specifications. The department is committed to challenging its pupils and providing a varied and engaging mathematical experience for them.

The programme of study for pupils consists of a two-year key stage three followed by our GCSEplus course. All students in Years 9 to 11 take part in an extended programme of study incorporating Level 2 Further Maths content, A level topics and structured investigations that further develop problem solving skills. The success and enthusiasm of the pupils leads to a high percentage continuing to A level. We currently have over 300 pupils studying maths in the sixth form, many of whom are also studying AS/A level further maths.

In addition, a significant number of pupils, some of exceptional calibre, go on to study mathematics or a related subject at university and we offer a special programme of support including preparation for entrance exams (such as MAT, TMUA and STEP) and interviews. Pupils are extremely successful as demonstrated by the examination results achieved year on year. Our results rank among the best of any school in the country.

Key Stage 3

• shape, space & measure
• data handling

Key Stage 4

• ratio, proportion and rates of change
• geometry and measures
• probability

Key Stage 5

Sixth form pupils study the OCR Mathematics (A) A Level specification. A Level Mathematics is a broad based mathematics course that covers the essential elements of pure mathematics and also covers applied mathematics through the study of statistics and mechanics. Pupils learn essential mathematical skills and processes whilst developing approaches to problem solving and mathematical argument, language and proof. Mathematical modelling techniques are also studied as approaches to solving applied mathematics problems in Statistics and Mechanics. In particular, there is a focus on the use of technology including the study of a large data set in statistics.

Further Mathematics

Sixth form pupils who take Further Mathematics study the OCR Further Mathematics (A) A Level specification .   The A Level Further Mathematics course is broader and deeper than A-level mathematics and introduces new mathematical concepts that have wide applications in engineering, physical sciences, economics and computing. The Pure Core provides the foundations for further mathematical study upon which learners study Statistics and Mechanics.  As per normal mathematics, there will also be overarching themes of mathematical argument, language and proof, mathematical problem solving and mathematical modelling that will be running throughout the course.

We provide a large number of extra-curricular opportunities for students and arrange for students to take part in the UKMT maths challenges, the UKMT Team Maths Challenge, the Hans Woyda Team maths tournament and special programmes for sixth form students who are planning to study maths or a related subject at university. There are also weekly problem solving clubs and a maths society that is run by 6th formers, all of which are very popular. We also promote “Puzzle of the Week”, “Parallel”, “Ritangle” and other competitions and have many students taking part. In addition, we run a series of Maths Circle lectures for sixth form students from local schools, often including talks from top university academics.

Maths Extra

• stuck on your homework
• not sure about a new topic
• trying to improve your maths in general

Maths Circle

2024 series of lectures: "the three doctors".

Each year we run a very successful programme of Maths Circle lectures which are open to 6th formers from all schools in the local area. Here are details of the 2024 lecture series. Click on image to download printable pdf

Quest for the Quintic, or Galois Theory

Synths, the Universe and Doodling

Differential Equations and how to solve them

Wilson’s school.

A boys’ grammar school in the London Borough of Sutton (UK), Wilson’s School is:

• committed to safeguarding and promoting the welfare of children and young people and expects all staff and volunteers to share this commitment
• a charitable company limited by guarantee registered in England and Wales (no. 7536970). Registered office: Mollison Drive, Wallington, Surrey SM6 9JW
• Publications
• School History
• Search this site
• Internal Mail
• Online Safety NSPCC
• Report a concern
• Report abuse CEOP
• Satchel One (Show My Homework)
• Wilson's Music
• Wilson's Sports
• 16-19 Bursary: application form
• 16-19 Bursary: guidelines
• Co-Curricular Offer
• Free school meals application form
• Lunch menus
• Permission to administer medicine

Leave of Absence Forms

• Junior and Middle School
• University Visit

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Enroll & Pay
• Media Interview Tips
• KU Communicator Resources
• Find a KU Faculty Expert
• When Experts Attack! podcast
• Hometown News

Intervention based on science of reading, math boosts comprehension, word problem-solving

Mon, 04/29/2024

Mike Krings

LAWRENCE — New research from the University of Kansas has found an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.

The intervention, performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students’ performance when compared to students who received general instruction. That indicates emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.

“Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems. This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems,” said Michael Orosco, professor of educational psychology at KU and lead author of the study. 

The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.

“It is proving to be one of the most effective evidence-based practices available for this growing population,” Orosco said.

The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice.

For the research, trained tutors developed the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem that explained a person made a quesadilla for his friend Mario, giving him one-fourth of it, then needed to students to determine how much remained.

The tutor first asked students if they remembered a class session in which they made quesadillas, what shape they were and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator, and explaining that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.

"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."

Orosco , director of KU’s Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario can impede subsequent problem-solving efforts.

The study proved effective in improving students’ problem-solving abilities, despite covariates including an individual’s basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key as, while ideally all students would begin on equal footing and there were little variations in a classroom, in reality, covariates exist and are commonplace.

The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.

The research builds on Orosco and colleagues’ work in understanding and improving math instruction for English learners . Future work will continue to examine the role of cognitive functions such as working memory and brain science , as well as potential integration of artificial intelligence in teaching math.

“Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems,” Orosco and Reed wrote. “Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition… Focusing on relevant language in word problems and providing collaborative support significantly improved students’ solution accuracy.”

Media Contacts

KU News Service

785-864-8860

[email protected]

share this!

April 29, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

trusted source

Intervention based on science of reading and math boosts comprehension and word problem-solving skills

by University of Kansas

New research from the University of Kansas has found that an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.

The intervention , performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students' performance when compared to students who received general instruction. This indicates that emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.

"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems . This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems," said Michael Orosco, professor of educational psychology at KU and lead author of the study.

The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.

"It is proving to be one of the most effective evidence-based practices available for this growing population," Orosco said.

The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice .

For the research, trained tutors implemented the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem explaining that a person made a quesadilla for his friend Mario and gave him one-fourth of it, then asked students to determine how much remained.

The tutor first asked students if they remembered a class session in which they made quesadillas and what shape they were, and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator. The tutor explains that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.

"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."

Orosco, director of KU's Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario could impede subsequent problem-solving efforts.

The study proved effective in improving students' problem-solving abilities, despite covariates including an individual's basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key, as while ideally all students would begin on equal footing and there would be few variations in a classroom, in reality, covariates exist and are commonplace.

The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.

The research builds on Orosco and colleagues' work in understanding and improving math instruction for English learners. Future work will continue to examine the role of cognitive functions such as working memory and brain science, as well as potential integration of artificial intelligence in teaching math.

"Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems," Orosco and Reed wrote. "Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition…. Focusing on relevant language in word problems and providing collaborative support significantly improved students' solution accuracy."

Provided by University of Kansas

Explore further

Feedback to editors

The BREAD Collaboration is searching for dark photons using a coaxial dish antenna

Research quantifies 'gap' in carbon removal for first time—shows countries need more awareness, ambition and action

2 hours ago

China sends a probe to get samples from the less-explored far side of the moon

4 hours ago

Research shows bumblebee nests are overheating due to climate change, threatening future populations

7 hours ago

Study finds human noise negatively impacts cricket survival and reproduction

14 hours ago

New eco-friendly lubricant additives protect turbine equipment, waterways

15 hours ago

Nanotubes, nanoparticles and antibodies detect tiny amounts of fentanyl

Bigger brains allow cliff-nesting seagull species to survive and thrive in urban environments

Oil palm plantations are driving massive downstream impact to watershed

16 hours ago

Centipedes used in traditional Chinese medicine offer leads for kidney treatment

Relevant physicsforums posts, physics instructor minimum education - community college.

10 hours ago

Studying "Useful" vs. "Useless" Stuff in School

Apr 30, 2024

Why are Physicists so informal with mathematics?

Apr 29, 2024

Plagiarism & ChatGPT: Is Cheating with AI the New Normal?

Apr 28, 2024

Digital oscilloscope for high school use

Apr 25, 2024

Motivating high school Physics students with Popcorn Physics

Apr 3, 2024

More from STEM Educators and Teaching

Related Stories

Study shows program improves teaching skills, students' word problem–solving

Jun 14, 2022

Study shows approach can help English learners improve at math word problems

Jun 19, 2018

Study examines role of working memory, cognitive functions in English learners learning to write

Oct 17, 2023

Cognitive study shows lack of bilingual education adversely affects English language learners' writing skills

Oct 14, 2021

How vocabulary breadth and depth influence bilingual reading comprehension

Aug 21, 2023

Study validates the simple view of reading for enhancing second and foreign language learners' experience

Aug 17, 2023

Recommended for you

Investigation reveals varied impact of preschool programs on long-term school success

17 hours ago

Training of brain processes makes reading more efficient

Apr 18, 2024

Researchers find lower grades given to students with surnames that come later in alphabetical order

Apr 17, 2024

Earth, the sun and a bike wheel: Why your high-school textbook was wrong about the shape of Earth's orbit

Apr 8, 2024

Touchibo, a robot that fosters inclusion in education through touch

Apr 5, 2024

More than money, family and community bonds prep teens for college success: Study

Let us know if there is a problem with our content.

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter