trig problem solving

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Trig Calculator

The sine and cosine trigonometric functions, tan, cot, sec, and csc, calculated from trig identities., trigonometry in a right triangle, other trigonometric calculators.

Welcome to this trigonometric calculator, a trig tool created to:

• Calculate any trigonometric function by inputting the angle at which you want to evaluate it; and
• Solve for the sides or angles of right triangles by using trigonometry.

Keep reading this article to learn more about trigonometric functions and the trig identities that relate them.

Trig functions are functions that take an angle as the argument. We define these functions by using the angle of a right triangle that is inserted in a unitary circle . Then, we relate that angle to the sides of such a triangle.

As the right triangle is circumscribed in a unit circle, the length of its hypotenuse equals the circle's radius (which equals one unit).

Sine and cosine are the fundamental trigonometric functions arising from the previous diagram:

• The sine of theta ( sin θ ) is the hypotenuse's vertical projection (green line); and
• The cosine of theta ( cos θ ) is the hypotenuse's horizontal projection (blue line).

We can rotate the radial line through the four quadrants and obtain the values of the trig functions from 0 to 360 degrees , as in the diagram below:

• For example, for an angle that leads to the second quadrant (90-180°), the cosine will be negative as the horizontal projection of the hypotenuse will point to the left. That's the case of 135°, whose cosine (horizontal projection, or x coordinate) equals -√2/2.
• For the third quadrant (180-270°), the cosine and the sine of the angles lying on it will be negative.
• For the fourth quadrant angles (270-360)°, the cosines will be positive and the sines negative.

Beyond 360 degrees

The previous behavior repeats cyclically, so trigonometric functions are not limited to 360°. We can keep rotating counterclockwise, and once we reach 360 degrees, the sine and cosine functions start to repeat the same behavior. As a consequence, we can relate the functions at different angles with the following trig identities for any n integer:

• sin(θ + 2πn) = sin(θ) ;
• cos(θ + 2πn) = cos(θ); and

For example a trig function at 90° (π/2) will be mathematically the same as at 450° (5π/2), as 5π/2 = π/2 + 2π.

Negative angles

Negative angles imply the same way to calculate sine and cosine (vertical and horizontal projections, respectively), with the difference that angular rotation occurs in the clockwise direction. For example, a trigonometric function at 270° is the same as at -90°, as their radial lines are the same (you can check it with this calculator)

Once you know the value of sine and cosine, you can use the following trigonometric identities to obtain the values of the other four functions:

Tangent is the sine-to-cosine ratio

tan(α) = sin(α)/cos(α)

Cosecant is the reciprocal of the sine

csc(α) = 1/sin(α)

Secant is the reciprocal of the cosine

sec(α) = 1/cos(α)

Cotangent is the reciprocal of the tangent

cot(α) = 1/tan(α)

From the previous analysis, we can obtain some valuable formulas that relate the angle of a right triangle to its sides. Of course, this doesn't limit to unit circles, so we can use it for hypotenuses of any length.

We relate the angle of the right triangle to its sides in the following way:

sin(α) = opposite/hypotenuse

cos(α) = adjacent/hypotenuse

tan(α) = opposite/adjacent

Remember that cotangent, secant, and cosecant are the inverse of the previous functions:

csc(α) = 1/sin(α) = hypotenuse/opposite

sec(α) = 1/cos(α) = hypotenuse/adjacent

cot(α) = 1/tan(α) = adjacent/opposite

You also can apply the previous formulas for the other acute angle ( β ), but consider that the legs of the triangle will switch: the adjacent will now be the hypotenuse and vice versa.

If you like this calculator, you may find these other tools interesting:

• Trigonometry calculator ;
• Cosine triangle calculator ;
• Sine triangle calculator ;
• Trig triangle calculator ;
• Right triangle trigonometry calculator ;
• Sine cosine tangent calculator ;
• Tangent ratio calculator ; and
• Tangent angle calculator .

How do I solve a 45-90-45 degree triangle by trig formulas?

If one leg of a 45 45 90 triangle is equal to a , then:

• The second leg also equals a ;
• The hypotenuse equals a √2 (from the hypotenuse formula c = √( a ² + a ²) = a √2 );
• The area is A = a ²/2 ; and
• The perimeter equals a (2 + √2) (the sum of the two sides plus the hypotenuse).

What are the values of the 6 trig functions at 90 degrees?

The values of the 6 trig functions for 90 degrees (π/2) are the following ones:

• sin(90°) = 1;
• cos(90°) = 0;
• tan(90°)= undefined;
• cot(90°) = 0;
• sec(90°) = undefined; and
• csc(90°) = 1.

Equation of a circle with diameter endpoints

Humans vs vampires, secretary problem (valentine's day), tensor product.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (294)
• Ecology (30)
• Everyday life (262)
• Finance (569)
• Health (440)
• Physics (509)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Solving Trigonometric Equations

• Last updated
• Save as PDF
• Page ID 61251

Learning Objectives

• Use the fundamental identities to solve trigonometric equations.
• Express trigonometric expressions in simplest form.
• Solve trigonometric equations by factoring.
• Solve trigonometric equations by using the Quadratic Formula.

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles , which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.

In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is \(2\pi\). In other words, every \(2\pi\) units, the y- values repeat. If we need to find all possible solutions, then we must add \(2\pi k\),where \(k\) is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is \(2\pi\):

\[\sin \theta=\sin(\theta \pm 2k\pi)\]

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Example \(\PageIndex{1A}\): Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation \(\cos \theta=\dfrac{1}{2}\).

From the unit circle, we know that

\[ \begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}\]

These are the solutions in the interval \([ 0,2\pi ]\). All possible solutions are given by

\[\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber\]

where \(k\) is an integer.

Example \(\PageIndex{1B}\): Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation \(\sin t=\dfrac{1}{2}\).

Solving for all possible values of \(t\) means that solutions include angles beyond the period of \(2\pi\). From the section on Sum and Difference Identities, we can see that the solutions are \(t=\dfrac{\pi}{6}\) and \(t=\dfrac{5\pi}{6}\). But the problem is asking for all possible values that solve the equation. Therefore, the answer is

\[t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber\]

How to: Given a trigonometric equation, solve using algebra

• Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
• Substitute the trigonometric expression with a single variable, such as \(x\) or \(u\).
• Solve the equation the same way an algebraic equation would be solved.
• Substitute the trigonometric expression back in for the variable in the resulting expressions.
• Solve for the angle.

Example \(\PageIndex{2}\): Solve the Linear Trigonometric Equation

Solve the equation exactly: \(2 \cos \theta−3=−5\), \(0≤\theta<2\pi\).

Use algebraic techniques to solve the equation.

\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]

Exercise \(\PageIndex{1}\)

Solve exactly the following linear equation on the interval \([0,2\pi)\): \(2 \sin x+1=0\).

\(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see [link]). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is \(\pi\),not \(2\pi\). Further, the domain of tangent is all real numbers with the exception of odd integer multiples of \(\dfrac{\pi}{2}\),unless, of course, a problem places its own restrictions on the domain.

Example \(\PageIndex{3A}\): Solving a Trignometric Equation Involving Sine

Solve the problem exactly: \(2 {\sin}^2 \theta−1=0\), \(0≤\theta<2\pi\).

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate \(\sin \theta\). Then we will find the angles.

\[\begin{align*} 2 {\sin}^2 \theta-1&= 0\\ 2 {\sin}^2 \theta&= 1\\ {\sin}^2 \theta&= \dfrac{1}{2}\\ \sqrt{ {\sin}^2 \theta }&= \pm \sqrt{ \dfrac{1}{2} }\\ \sin \theta&= \pm \dfrac{1}{\sqrt{2}}\\ &= \pm \dfrac{\sqrt{2}}{2}\\ \theta&= \dfrac{\pi}{4}, \space \dfrac{3\pi}{4},\space \dfrac{5\pi}{4}, \space \dfrac{7\pi}{4} \end{align*}\]

As \(\sin \theta=−\dfrac{1}{2}\), notice that all four solutions are in the third and fourth quadrants.

Example \(\PageIndex{3B}\): Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: \(\csc \theta=−2\), \(0≤\theta<4\pi\).

We want all values of \(\theta\) for which \(\csc \theta=−2\) over the interval \(0≤\theta<4\pi\).

\[\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}\]

Example \(\PageIndex{3C}\): Solving an Equation Involving Tangent

Solve the equation exactly: \(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\), \(0≤\theta<2\pi\).

Recall that the tangent function has a period of \(\pi\). On the interval \([ 0,\pi )\),and at the angle of \(\dfrac{\pi}{4}\),the tangent has a value of \(1\). However, the angle we want is \(\left(\theta−\dfrac{\pi}{2}\right)\). Thus, if \(\tan\left(\dfrac{\pi}{4}\right)=1\),then

\[\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}\]

Over the interval \([ 0,2\pi )\),we have two solutions:

\(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}\)

Exercise \(\PageIndex{2}\)

Find all solutions for \(\tan x=\sqrt{3}\).

\(\dfrac{\pi}{3}\pm \pi k\)

Example \(\PageIndex{4}\): Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation \(2(\tan x+3)=5+\tan x\), \(0≤x<2\pi\).

We can solve this equation using only algebra. Isolate the expression \(\tan x\) on the left side of the equals sign.

There are two angles on the unit circle that have a tangent value of \(−1\): \(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{7\pi}{4}\).

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Example \(\PageIndex{5A}\): Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation \(\sin \theta=0.8\),where \(\theta\) is in radians.

Make sure mode is set to radians. To find \(\theta\), use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the \({\sin}^{−1}\) function. What is shown on the screen is \({\sin}^{−1}\).The calculator is ready for the input within the parentheses. For this problem, we enter \({\sin}^{−1}(0.8)\), and press ENTER. Thus, to four decimals places,

\({\sin}^{−1}(0.8)≈0.9273\)

The solution is

\(\theta≈0.9273\pm 2\pi k\)

The angle measurement in degrees is

\[\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}\]

Note that a calculator will only return an angle in quadrants I or IV for the sine function since that is the range of the inverse sine. The other angle is obtained by using \(\pi−\theta\).

Example \(\PageIndex{5B}\): Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation \( \sec θ=−4, \) giving your answer in radians.

We can begin with some algebra.

\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]

Check that the MODE is in radians. Now use the inverse cosine function

\[\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}\]

Since \(\dfrac{\pi}{2}≈1.57\) and \(\pi≈3.14\),\(1.8235\) is between these two numbers, thus \(\theta≈1.8235\) is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See Figure \(\PageIndex{2}\).

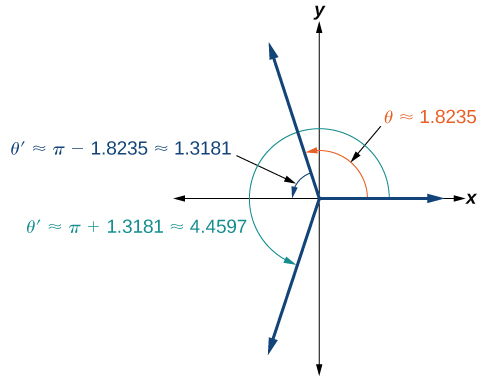
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is \(\theta '≈\pi−1.8235≈1.3181\). The other solution in quadrant III is \(\theta '≈\pi+1.3181≈4.4597\).

The solutions are \(\theta≈1.8235\pm 2\pi k\) and \(\theta≈4.4597\pm 2\pi k\).

Exercise \(\PageIndex{3}\)

Solve \(\cos \theta=−0.2\).

\(\theta≈1.7722\pm 2\pi k\) and \(\theta≈4.5110\pm 2\pi k\)

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as \(x\) or \(u\). If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Example \(\PageIndex{6A}\): Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: \({\cos}^2 \theta+3 \cos \theta−1=0\), \(0≤\theta<2\pi\).

We begin by using substitution and replacing \(\cos \theta\) with \(x\). It is not necessary to use substitution, but it may make the problem easier to solve visually. Let \(\cos \theta=x\). We have

\(x^2+3x−1=0\)

The equation cannot be factored, so we will use the quadratic formula: \(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).

\[\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}\]

Replace \(x\) with \(\cos \theta \) and solve.

\[\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}\]

Note that only the + sign is used. This is because we get an error when we solve \(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) on a calculator, since the domain of the inverse cosine function is \([ −1,1 ]\). However, there is a second solution:

\[\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}\]

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

\[\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}\]

Example \(\PageIndex{6B}\): Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: \(2 {\sin}^2 \theta−5 \sin \theta+3=0\), \(0≤\theta≤2\pi\).

Using grouping, this quadratic can be factored. Either make the real substitution, \(\sin \theta=u\),or imagine it, as we factor:

\[\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}\]

Next solve for \(\theta\): \(\sin \theta≠\dfrac{3}{2}\), as the range of the sine function is \([ −1,1 ]\). However, \(\sin \theta=1\), giving the solution \(\theta=\dfrac{\pi}{2}\).

Make sure to check all solutions on the given domain as some factors have no solution.

Exercise \(\PageIndex{4}\)

Solve \({\sin}^2 \theta=2 \cos \theta+2\), \(0≤\theta≤2\pi\). [Hint: Make a substitution to express the equation only in terms of cosine.]

\(\cos \theta=−1\), \(\theta=\pi\)

Example \(\PageIndex{7A}\): Solving a Trigonometric Equation Using Algebra

Solve exactly: \(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)

This problem should appear familiar as it is similar to a quadratic. Let \(\sin \theta=x\). The equation becomes \(2x^2+x=0\). We begin by factoring:

\[\begin{align*} 2x^2+x&= 0\\ x(2x+1)&= 0\qquad \text {Set each factor equal to zero.}\\ x&= 0\\ 2x+1&= 0\\ x&= -\dfrac{1}{2} \end{align*}\] Then, substitute back into the equation the original expression \(\sin \theta \) for \(x\). Thus, \[\begin{align*} \sin \theta&= 0\\ \theta&= 0,\pi\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]

The solutions within the domain \(0≤\theta<2\pi\) are \(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

\[\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]

We can see the solutions on the graph in Figure \(\PageIndex{3}\). On the interval \(0≤\theta<2\pi\),the graph crosses the \(x\) - axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

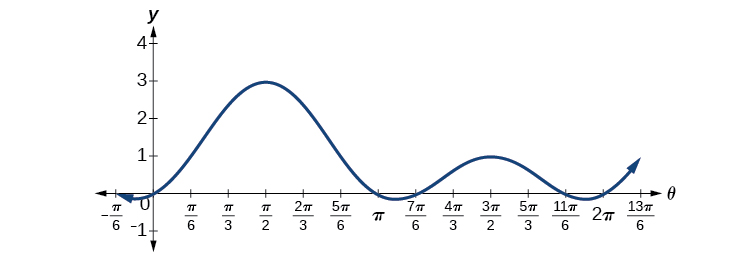
We can verify the solutions on the unit circle in via the result in the section on Sum and Difference Identities as well.

Example \(\PageIndex{7B}\): Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: \(2 {\sin}^2 \theta−3 \sin \theta+1=0\), \(0≤\theta<2\pi\).

We can factor using grouping. Solution values of \(\theta\) can be found on the unit circle.

\[\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}\]

Exercise \(\PageIndex{5}\)

Solve the quadratic equation \(2{\cos}^2 \theta+\cos \theta=0\).

\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Example \(\PageIndex{8}\): Solving an Equation Using an Identity

Solve the equation exactly using an identity: \(3 \cos \theta+3=2 {\sin}^2 \theta\), \(0≤\theta<2\pi\).

If we rewrite the right side, we can write the equation in terms of cosine:

\[\begin{align*} 3 \cos \theta+3&= 2 {\sin}^2 \theta\\ 3 \cos \theta+3&= 2(1-{\cos}^2 \theta)\\ 3 \cos \theta+3&= 2-2{\cos}^2 \theta\\ 2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\ (2 \cos \theta+1)(\cos \theta+1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}\\ \cos \theta+1&= 0\\ \cos \theta&= -1\\ \theta&= \pi\\ \end{align*}\]

Our solutions are \(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as \(\sin(2x)\) or \(\cos(3x)\). When confronted with these equations, recall that \(y=\sin(2x)\) is a horizontal compression by a factor of 2 of the function \(y=\sin x\). On an interval of \(2\pi\),we can graph two periods of \(y=\sin(2x)\),as opposed to one cycle of \(y=\sin x\). This compression of the graph leads us to believe there may be twice as many x -intercepts or solutions to \(\sin(2x)=0\) compared to \(\sin x=0\). This information will help us solve the equation.

Example \(\PageIndex{9}\): Solving a Multiple Angle Trigonometric Equation

Solve exactly: \(\cos(2x)=\dfrac{1}{2}\) on \([ 0,2\pi )\).

We can see that this equation is the standard equation with a multiple of an angle. If \(\cos(\alpha)=\dfrac{1}{2}\),we know \(\alpha\) is in quadrants I and IV. While \(\theta={\cos}^{−1} \dfrac{1}{2}\) will only yield solutions in quadrants I and II, we recognize that the solutions to the equation \(\cos \theta=\dfrac{1}{2}\) will be in quadrants I and IV.

Therefore, the possible angles are \(\theta=\dfrac{\pi}{3}\) and \(\theta=\dfrac{5\pi}{3}\). So, \(2x=\dfrac{\pi}{3}\) or \(2x=\dfrac{5\pi}{3}\), which means that \(x=\dfrac{\pi}{6}\) or \(x=\dfrac{5\pi}{6}\). Does this make sense? Yes, because \(\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\).

Are there any other possible answers? Let us return to our first step.

In quadrant I, \(2x=\dfrac{\pi}{3}\), so \(x=\dfrac{\pi}{6}\) as noted. Let us revolve around the circle again:

\[\begin{align*} 2x&= \dfrac{\pi}{3}+2\pi\\ &= \dfrac{\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{7\pi}{3}\\ x&= \dfrac{7\pi}{6}\\ \text {One more rotation yields}\\ 2x&= \dfrac{\pi}{3}+4\pi\\ &= \dfrac{\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{13\pi}{3}\\ \end{align*}\]

\(x=\dfrac{13\pi}{6}>2\pi\), so this value for \(x\) is larger than \(2\pi\), so it is not a solution on \([ 0,2\pi )\).

In quadrant IV, \(2x=\dfrac{5\pi}{3}\), so \(x=\dfrac{5\pi}{6}\) as noted. Let us revolve around the circle again:

\[\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}\]

so \(x=\dfrac{11\pi}{6}\).

One more rotation yields

\[\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}\]

\(x=\dfrac{17\pi}{6}>2\pi\),so this value for \(x\) is larger than \(2\pi\),so it is not a solution on \([ 0,2\pi )\)  .

Our solutions are \(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\), and \(\dfrac{11\pi}{6}\). Note that whenever we solve a problem in the form of \(sin(nx)=c\), we must go around the unit circle \(n\) times.

Key Concepts

• When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution. See Example \(\PageIndex{1}\), Example \(\PageIndex{2}\), and Example \(\PageIndex{3}\).
• Equations involving a single trigonometric function can be solved or verified using the unit circle. See Example \(\PageIndex{4}\), Example \(\PageIndex{5}\), and Example \(\PageIndex{6}\), and Example \(\PageIndex{7}\).
• We can also solve trigonometric equations using a graphing calculator. See Example \(\PageIndex{8}\) and Example \(\PageIndex{9}\).
• Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc. See Example \(\PageIndex{10}\), Example \(\PageIndex{11}\), Example \(\PageIndex{12}\), and Example \(\PageIndex{13}\).
• We can also use the identities to solve trigonometric equation. See Example \(\PageIndex{14}\), Example \(\PageIndex{15}\), and Example \(\PageIndex{16}\).
• We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval. See Example \(\PageIndex{17}\).
• Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions. See Example \(\PageIndex{18}\).

Contributors and Attributions

Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a  Creative Commons Attribution License 4.0  license. Download for free at  https://openstax.org/details/books/precalculus .

Trigonometric Word Problems

In these lessons, examples, and solutions we will learn the trigonometric functions (sine, cosine, tangent) and how to solve word problems using trigonometry.

Related Pages Trigonometry Word Problems Lessons On Trigonometry Inverse trigonometry Trigonometry Worksheets

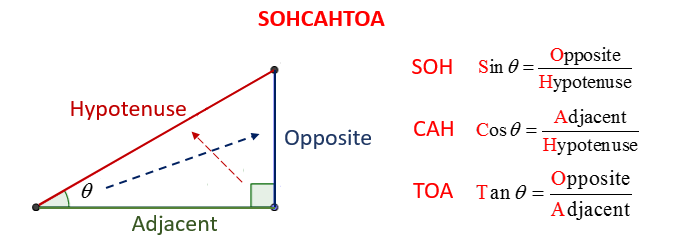
The following diagram shows how SOHCAHTOA can help you remember how to use sine, cosine, or tangent to find missing angles or missing sides in a trigonometry problem. Scroll down the page for examples and solutions.

How To Solve Trigonometry Problems Or Questions?

Step 1: If no diagram is given, draw one yourself. Step 2: Mark the right angles in the diagram. Step 3: Show the sizes of the other angles and the lengths of any lines that are known. Step 4: Mark the angles or sides you have to calculate. Step 5: Consider whether you need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles. Step 6: Decide whether you will need the Pythagorean theorem, sine, cosine or tangent. Step 7: Check that your answer is reasonable. The hypotenuse is the longest side in a right triangle.

How To Use Cosine To Calculate The Side Of A Right Triangle?

Solution: Use the Pythagorean theorem to evaluate the length of PR.

How To Use Tangent To Calculate The Side Of A Triangle?

Calculate the length of the side x, given that tan θ = 0.4

How To Use Sine To Calculate The Side Of A Triangle?

Calculate the length of the side x, given that sin θ = 0.6

How To Solve Word Problems Using Trigonometry?

The following video shows how to use the trigonometric ratio, tangent, to find the height of a balloon.

How To Solve Word Problems Using Sine?

This video shows how to use the trigonometric ratio, sine, to find the elevation gain of a hiker going up a slope.

Example: A hiker is hiking up a 12 degrees slope. If he hikes at a constant rate of 3 mph, how much altitude does he gain in 5 hours of hiking?

How To Use Cosine To Solve A Word Problem?

Example: A ramp is pulled out of the back of truck. There is a 38 degrees angle between the ramp and the pavement. If the distance from the end of the ramp to to the back of the truck is 10 feet. How long is the ramp? Step 1: Find the values of the givens. Step 2: Substitute the values into the cosine ratio. Step 3: Solve for the missing side. Step 4: Write the units

How To Solve Word Problems Using Tangent?

The following video shows how to use trigonometric ratio, tangent, to find the height of a building.

How To Solve Trigonometry Word Problems Using Tangent?

Example: Neil sees a rocket at an angle of elevation of 11 degrees. If Neil is located at 5 miles from the rocket launch pad, how high is the rocket?

How To Determining The Speed Of A Boat Using Trigonometry?

Example: A balloon is hovering 800 ft above a lake. The balloon is observed by the crew of a boat as they look upwards at an angle of 0f 20 degrees. 25 seconds later, the crew had to look at an angle of 65 degrees to see the balloon. How fast was the boat traveling?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Free Mathematics Tutorials

Solve Trigonometry Problems

Popular pages.

• Trigonometry Problems and Questions with Solutions - Grade 10
• Free Trigonometry Questions with Answers
• Free Trigonometry Tutorials and Problems
• Trigonometry Problems and Questions with Solutions - Grade 11
• Trigonometry Problems and Questions with Solutions - Grade 12
• Privacy Policy

Game Central

Introduction to Trigonometry

Trigonometry (from Greek trigonon "triangle" + metron "measure")

Want to learn Trigonometry? Here is a quick summary. Follow the links for more, or go to Trigonometry Index

Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more!

Right-Angled Triangle

The triangle of most interest is the right-angled triangle . The right angle is shown by the little box in the corner:

Another angle is often labeled θ , and the three sides are then called:

• Adjacent : adjacent (next to) the angle θ
• Opposite : opposite the angle θ
• and the longest side is the Hypotenuse

Why a Right-Angled Triangle?

Why is this triangle so important?

Imagine we can measure along and up but want to know the direct distance and angle:

Trigonometry can find that missing angle and distance.

Or maybe we have a distance and angle and need to "plot the dot" along and up:

Questions like these are common in engineering, computer animation and more.

And trigonometry gives the answers!

Sine, Cosine and Tangent

The main functions in trigonometry are Sine, Cosine and Tangent

They are simply one side of a right-angled triangle divided by another.

For any angle " θ ":

(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan .)

Example: What is the sine of 35°?

Using this triangle (lengths are only to one decimal place):

sin(35°) = Opposite Hypotenuse = 2.8 4.9 = 0.57...

The triangle could be larger, smaller or turned around, but that angle will always have that ratio .

Calculators have sin, cos and tan to help us, so let's see how to use them:

Example: How Tall is The Tree?

We can't reach the top of the tree, so we walk away and measure an angle (using a protractor) and distance (using a laser):

• We know the Hypotenuse
• And we want to know the Opposite

Sine is the ratio of Opposite / Hypotenuse :

sin(45°) = Opposite Hypotenuse

Get a calculator, type in "45", then the "sin" key:

sin(45°) = 0.7071...

What does the 0.7071... mean? It is the ratio of the side lengths, so the Opposite is about 0.7071 times as long as the Hypotenuse.

We can now put 0.7071... in place of sin(45°):

0.7071... = Opposite Hypotenuse

And we also know the hypotenuse is 20 :

0.7071... = Opposite 20

To solve, first multiply both sides by 20:

20 × 0.7071... = Opposite

Opposite = 14.14m (to 2 decimals)

The tree is 14.14m tall

Try Sin Cos and Tan

Play with this for a while (move the mouse around) and get familiar with values of sine, cosine and tangent for different angles, such as 0°, 30°, 45°, 60° and 90°.

Also try 120°, 135°, 180°, 240°, 270° etc, and notice that positions can be positive or negative by the rules of Cartesian coordinates , so the sine, cosine and tangent change between positive and negative also.

So trigonometry is also about circles !

Unit Circle

What you just played with is the Unit Circle .

It is a circle with a radius of 1 with its center at 0.

Because the radius is 1, we can directly measure sine, cosine and tangent.

Here we see the sine function being made by the unit circle:

Note: you can see the nice graphs made by sine, cosine and tangent .

Degrees and Radians

Angles can be in Degrees or Radians . Here are some examples:

Repeating Pattern

Because the angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation (see Amplitude, Period, Phase Shift and Frequency ).

When we want to calculate the function for an angle larger than a full rotation of 360° (2 π radians) we subtract as many full rotations as needed to bring it back below 360° (2 π radians):

Example: what is the cosine of 370°?

370° is greater than 360° so let us subtract 360°

370° − 360° = 10°

cos(370°) = cos(10°) = 0.985 (to 3 decimal places)

And when the angle is less than zero, just add full rotations.

Example: what is the sine of −3 radians?

−3 is less than 0 so let us add 2 π radians

−3 + 2 π = −3 + 6.283... = 3.283... rad ians

sin(−3) = sin(3.283...) = −0.141 (to 3 decimal places)

Solving Triangles

Trigonometry is also useful for general triangles, not just right-angled ones .

It helps us in Solving Triangles . "Solving" means finding missing sides and angles.

Example: Find the Missing Angle "C"

Angle C can be found using angles of a triangle add to 180° :

So C = 180° − 76° − 34° = 70°

We can also find missing side lengths. The general rule is:

When we know any 3 of the sides or angles we can find the other 3 (except for the three angles case)

See Solving Triangles for more details.

Other Functions (Cotangent, Secant, Cosecant)

Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Trigonometric and Triangle Identities

And as you get better at Trigonometry you can learn these:

Enjoy becoming a triangle (and circle) expert!

Math teaching support you can trust

resources downloaded

one-on-one tutoring sessions

schools supported

[FREE] Fun Math Games & Activities

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5!

15 Trigonometry Questions And Practice Problems To Do With High Schoolers

Beki christian.

Trigonometry questions address the relationship between the angles of a triangle and the lengths of the sides. By using our knowledge of the rules of trigonometry and trigonometric functions, we can calculate missing angles or sides when we have been given some of the information. 

Here we’ve provided 15 trigonometry questions that will help your students practice the various types of trigonometry questions they will encounter during high school.

Trigonometry in the real world

Trigonometry in high school, how to answer trigonometry questions: right angled triangles, how to answer trigonometry questions: non-right triangles, trigonometry questions: missing side, trigonometry questions: missing angles, trigonometry questions: sohcahtoa, trigonometry questions: exact values, trigonometry questions: 3d trigonometry, trigonometry questions: sine/cosine rule, trigonometry questions – area of a triangle.

Trigonometry is used by architects, engineers, astronomers, crime scene investigators, flight engineers and many others.

Trigonometry Check for Understanding Quiz

Wondering if your students have fully grasped trigonometry? Use this quiz to check their understanding across 15 questions with answers covering all things trigonometry!

In trigonometry we learn about the sine function, tangent function, and cosine function. These trig functions are abbreviated as sin, cos, and tan. We can use these to calculate sides and angles in right angled triangles. Later, students will be applying this to a variety of situations as well as learning the exact values of sin, cos, and tan for certain angles.

Students learn about trigonometric ratios: the law of sines, law of cosines, a new formula for the area of a triangle and applying trigonometric theorems to 3D shapes.

Trigonometry for more senior high school students will introduce the reciprocal trig functions, cotangent, secant and cosecant, but you don’t have to worry about these right now!

How to answer trigonometry questions

The way to answer trigonometry questions depends on whether it is a right angled triangle or not.

If your trigonometry question involves a right angled triangle, you can apply the following relationships, ie SOH, CAH, TOA

sin θ = opposite/hypotenuse

cos θ = adjacent/hypotenuse 

tan θ = opposite/adjacent

The acronym SOH CAH TOA is used so that you can remember which ratio to use.

To answer the trigonometry question:

• Establish that it is a right angled triangle.
• Label the opposite side (opposite the angle) the adjacent side (next to the angle) and the hypotenuse (longest side opposite the right angle).

3. Use the following triangles to help us decide which calculation to do:

If the triangle is not a right angled triangle then we need to use the sine rule or the cosine rule. 

There is also a formula we can use for the area of a triangle, which does not require us to know the base and height of the triangle.

Sine rule: \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}

Cosine rule: a^{2}=b^{2}+c^{2}-2bc \cos(A)

Area of a triangle: Area = \frac{1}{2}ab \sin(C)

• Establish that it is not a right angled triangle.
• Label the sides of the triangle using lowercase a, b, c.
• Label the angles of the triangle using upper case A, B and C.
• Opposite sides and angles should use the same letter, for example, angle A is opposite to side a.

Trigonometry questions

In high school geometry, trigonometry questions focus on the understanding of sin, cos, and tan (SOHCAHTOA) to calculate missing sides and angles in right triangles. 

1. A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10^{\circ} to the horizontal. Calculate the length of the zip wire.

2. A surveyor wants to know the height of a skyscraper. He places his inclinometer on a tripod 1m from the ground. At a distance of 50m from the skyscraper, he records an angle of elevation of 82^{\circ} .

What is the height of the skyscraper? Give your answer to one decimal place.

Total height = 355.8+1=356.8m.

3. Triangle ABC is isosceles. Calculate the height of triangle ABC.

To solve this we split the triangle into two right angled triangles.

4. A builder is constructing a roof. The wood he is using for the sloped section of the roof is 4m long and the peak of the roof needs to be 2m high. What angle should the piece of wood make with the base of the roof?

5. A ladder is leaning against a wall. The ladder is 1.8m long and the bottom of the ladder is 0.5m from the base of the wall. To be considered safe, a ladder must form an angle of between 70^{\circ} and 80^{\circ} with the floor. Is this ladder safe?

Not enough information

Yes it is safe.

6. A helicopter flies 40km east followed by 105km south. On what bearing must the helicopter fly to return home directly?

Since bearings are measured clockwise from North, we need to do 360-21=339^{\circ}.

In geometry, trigonometry questions ask students to solve a variety of problems including multi-step problems and real-life problems. We also need to be familiar with the exact values of the trigonometric functions at certain angles. 

We look at applying trigonometry to 3D problems as well as using the sine rule, cosine rule, and area of a triangle.

7.  Calculate the size of angle ABC. Give your answer to 3 significant figures.

8. Kevin’s garden is in the shape of an isosceles trapezoid (the sloping sides are equal in length). Kevin wants to buy enough grass seed for his garden. Each box of grass seed covers 15m^2 . How many boxes of grass seed will Kevin need to buy?

To calculate the area of the trapezoid, we first need to find the height. Since it is an isosceles trapezium, it is symmetrical and we can create a right angled triangle with a base of \frac{10-5}{2} .

We can then find the area of the trapezoid:

Number of boxes: 88.215=5.88

Kevin will need 6 boxes.

9.   Which of these values cannot be the value of \sin(\theta) ?

10. . Write 4sin(60) + 3tan(60) in the form a\sqrt{k}.

11. Work out angle a, between the line AG and the plane ADHE.

We need to begin by finding the length AH by looking at the triangle AEH and using pythagorean theorem.

We can then find angle a by looking at the triangle AGH.

12.   Work out the length of BC.

First we need to find the length DC by looking at triangle CDE.

We can then look at triangle BAC.

13. Ship A sails 40km due West and ship B sails 65km on a bearing of 050^{\circ} . Find the distance between the two ships.

The angle between their two paths is 90+50=140^{\circ} .

\begin{aligned} a^{2}&=b^{2}+c^{2}-2bc \cos(A)\\\\ a^{2}&=40^{2}+65^{2}-2\times 40 \times 65 \cos(140)\\\\ a^{2}&=5825-5200 \cos(140)\\\\ a^{2}&=9808.43\\\\ a&=99.0\mathrm{km} \end{aligned}

14.   Find the size of angle B.

First we need to look at the right angled triangle.

Then we can look at the scalene triangle.

15. The area of the triangle is 16cm^2 . Find the length of the side x .

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\\\ 16&=\frac{1}{2} \times x \times 2x \times \sin(40)\\\\ 16&=x^{2} \sin(40)\\\\ \frac{1}{\sin(40)}&=x^{2}\\\\ 24.89&=x^{2}\\\\ 5.0&=x \end{aligned}

Looking for more high school trigonometry math questions and word problems?

• Ratio questions
• Algebra questions
• Probability questions
• Venn diagram questions
• Long division questions
• Pythagorean theorem questions

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by secondary school maths teacher Beki Christian and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.

Pythagoras Theorem Questions [FREE]

Downloadable Pythagoras theorem worksheet containing 15 multiple choice questions with a mix of worded problems and deeper problem solving questions.

Includes an answer key and follows variation theory with plenty of opportunities for students to work independently at their own level.

Privacy Overview

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Search IntMath
• Math interactives
• About (site info)
• Uses of Trignometry
• ASCIIMath input, KaTeX output
• ASCIIMath input, LaTeX and KaTeX output
• Send Math in emails
• Syntax for ASCIIMathML
• Math Display Experiments
• Scientific Notebook
• Math Problem Solver

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Trigonometry Problem Solver

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.

Sign up for free here .

Problem Solver Subjects

Our math problem solver that lets you input a wide variety of trigonometry math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.

• Math Word Problems
• Pre-Algebra
• Geometry Graphing
• Trigonometry
• Precalculus
• Finite Math
• Linear Algebra

Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.

Basic Math Solutions

Below are examples of basic math problems that can be solved.

• Long Arithmetic
• Rational Numbers
• Operations with Fractions
• Ratios, Proportions, Percents
• Measurement, Area, and Volume
• Factors, Fractions, and Exponents
• Unit Conversions
• Data Measurement and Statistics
• Points and Line Segments

Math Word Problem Solutions

Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.

Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?

Simplified Equation: 17 - x = 8

Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?

Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)

Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}

Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?

Simplified: 40 - 10 - 5

Pre-Algebra Solutions

Below are examples of Pre-Algebra math problems that can be solved.

• Variables, Expressions, and Integers
• Simplifying and Evaluating Expressions
• Solving Equations
• Multi-Step Equations and Inequalities
• Ratios, Proportions, and Percents
• Linear Equations and Inequalities

Algebra Solutions

Below are examples of Algebra math problems that can be solved.

• Algebra Concepts and Expressions
• Points, Lines, and Line Segments
• Simplifying Polynomials
• Factoring Polynomials
• Linear Equations
• Absolute Value Expressions and Equations
• Radical Expressions and Equations
• Systems of Equations
• Quadratic Equations
• Inequalities
• Complex Numbers and Vector Analysis
• Logarithmic Expressions and Equations
• Exponential Expressions and Equations
• Conic Sections
• Vector Spaces
• 3d Coordinate System
• Eigenvalues and Eigenvectors
• Linear Transformations
• Number Sets
• Analytic Geometry

Trigonometry Solutions

Below are examples of Trigonometry math problems that can be solved.

• Algebra Concepts and Expressions Review
• Right Triangle Trigonometry
• Radian Measure and Circular Functions
• Graphing Trigonometric Functions
• Simplifying Trigonometric Expressions
• Verifying Trigonometric Identities
• Solving Trigonometric Equations
• Complex Numbers
• Analytic Geometry in Polar Coordinates
• Exponential and Logarithmic Functions
• Vector Arithmetic

Precalculus Solutions

Below are examples of Precalculus math problems that can be solved.

• Operations on Functions
• Rational Expressions and Equations
• Polynomial and Rational Functions
• Analytic Trigonometry
• Sequences and Series
• Analytic Geometry in Rectangular Coordinates
• Limits and an Introduction to Calculus

Calculus Solutions

Below are examples of Calculus math problems that can be solved.

• Evaluating Limits
• Derivatives
• Applications of Differentiation
• Applications of Integration
• Techniques of Integration
• Parametric Equations and Polar Coordinates
• Differential Equations

Statistics Solutions

Below are examples of Statistics problems that can be solved.

• Algebra Review
• Average Descriptive Statistics
• Dispersion Statistics
• Probability
• Probability Distributions
• Frequency Distribution
• Normal Distributions
• t-Distributions
• Hypothesis Testing
• Estimation and Sample Size
• Correlation and Regression

Finite Math Solutions

Below are examples of Finite Math problems that can be solved.

• Polynomials and Expressions
• Equations and Inequalities
• Linear Functions and Points
• Systems of Linear Equations
• Mathematics of Finance
• Statistical Distributions

Linear Algebra Solutions

Below are examples of Linear Algebra math problems that can be solved.

• Introduction to Matrices
• Linear Independence and Combinations

Chemistry Solutions

Below are examples of Chemistry problems that can be solved.

• Unit Conversion
• Atomic Structure
• Molecules and Compounds
• Chemical Equations and Reactions
• Behavior of Gases
• Solutions and Concentrations

Physics Solutions

Below are examples of Physics math problems that can be solved.

• Static Equilibrium
• Dynamic Equilibrium
• Kinematics Equations
• Electricity
• Thermodymanics

Geometry Graphing Solutions

Below are examples of Geometry and graphing math problems that can be solved.

• Step By Step Graphing
• Linear Equations and Functions
• Polar Equations

Looking for the old Mathway Calculator? We've moved it to here .

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of GPT large language models to parse and generate natural language. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor. Learn More.

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Trigonometry

About this unit.

Knowing trig identities is one thing, but being able to prove them takes us to another level. In this unit, we'll prove various trigonometric identities and define inverse trigonometric functions, which allow us to solve trigonometric equations.

Special trigonometric values in the first quadrant

• Cosine, sine and tangent of π/6 and π/3 (Opens a modal)
• Trig values of π/4 (Opens a modal)
• Trig values of π/6, π/4, and π/3 Get 3 of 4 questions to level up!

Trigonometric identities on the unit circle

• Sine & cosine identities: symmetry (Opens a modal)
• Tangent identities: symmetry (Opens a modal)
• Sine & cosine identities: periodicity (Opens a modal)
• Tangent identities: periodicity (Opens a modal)
• Trig identities from reflections and rotations Get 3 of 4 questions to level up!
• Trig values of special angles Get 3 of 4 questions to level up!

Inverse trigonometric functions

• Intro to arcsine (Opens a modal)
• Intro to arctangent (Opens a modal)
• Intro to arccosine (Opens a modal)
• Restricting domains of functions to make them invertible (Opens a modal)
• Domain & range of inverse tangent function (Opens a modal)
• Using inverse trig functions with a calculator (Opens a modal)
• Inverse trigonometric functions review (Opens a modal)
• Evaluate inverse trig functions Get 3 of 4 questions to level up!

Law of sines

• Solving for a side with the law of sines (Opens a modal)
• Solving for an angle with the law of sines (Opens a modal)
• Proof of the law of sines (Opens a modal)
• Solve triangles using the law of sines Get 3 of 4 questions to level up!

Law of cosines

• Solving for a side with the law of cosines (Opens a modal)
• Solving for an angle with the law of cosines (Opens a modal)
• Proof of the law of cosines (Opens a modal)
• Solve triangles using the law of cosines Get 3 of 4 questions to level up!

Solving general triangles

• Trig word problem: stars (Opens a modal)
• Laws of sines and cosines review (Opens a modal)
• General triangle word problems Get 3 of 4 questions to level up!

Sinusoidal equations

• Solving sinusoidal equations of the form sin(x)=d (Opens a modal)
• Cosine equation algebraic solution set (Opens a modal)
• Cosine equation solution set in an interval (Opens a modal)
• Sine equation algebraic solution set (Opens a modal)
• Solving cos(θ)=1 and cos(θ)=-1 (Opens a modal)
• Solve sinusoidal equations (basic) Get 3 of 4 questions to level up!
• Solve sinusoidal equations Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting solutions of trigonometric equations (Opens a modal)
• Trig word problem: solving for temperature (Opens a modal)
• Trigonometric equations review (Opens a modal)
• Interpret solutions of trigonometric equations in context Get 3 of 4 questions to level up!
• Sinusoidal models word problems Get 3 of 4 questions to level up!

Angle addition identities

• Trig angle addition identities (Opens a modal)
• Using the cosine angle addition identity (Opens a modal)
• Using the cosine double-angle identity (Opens a modal)
• Proof of the sine angle addition identity (Opens a modal)
• Proof of the cosine angle addition identity (Opens a modal)
• Proof of the tangent angle sum and difference identities (Opens a modal)
• Using the trig angle addition identities Get 3 of 4 questions to level up!

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.

trig-calculator

• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Trigonometry : Solving Word Problems with Trigonometry

Study concepts, example questions & explanations for trigonometry, all trigonometry resources, example questions, example question #1 : solving word problems with trigonometry.

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

You can draw the following right triangle from the information given in the question:

In order to find out how far up the ladder goes, you will need to use sine.

In right triangle ABC, where angle A measures 90 degrees, side AB measures 15 and side AC measures 36, what is the length of side BC?

This triangle cannot exist.

Example Question #5 : Solving Word Problems With Trigonometry

A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25 o angle with the ground. How long is the wire, w? Round your answer to two decimal places.

23.81 meters

28.31 meters

21.83 meters

To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25 o , the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w. 

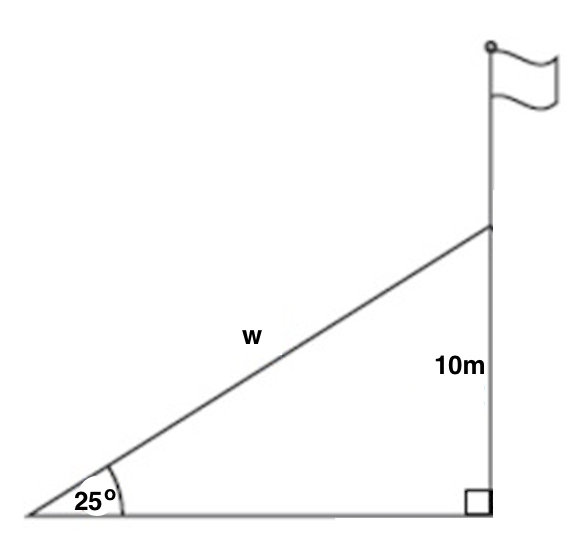
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25 o . 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.

We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:

To solve this problem instead using the cosecant function, we would get:

The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem. 

Example Question #6 : Solving Word Problems With Trigonometry

When the sun is 22 o above the horizon, how long is the shadow cast by a building that is 60 meters high?

To solve this problem, first set up a diagram that shows all of the info given in the problem. 

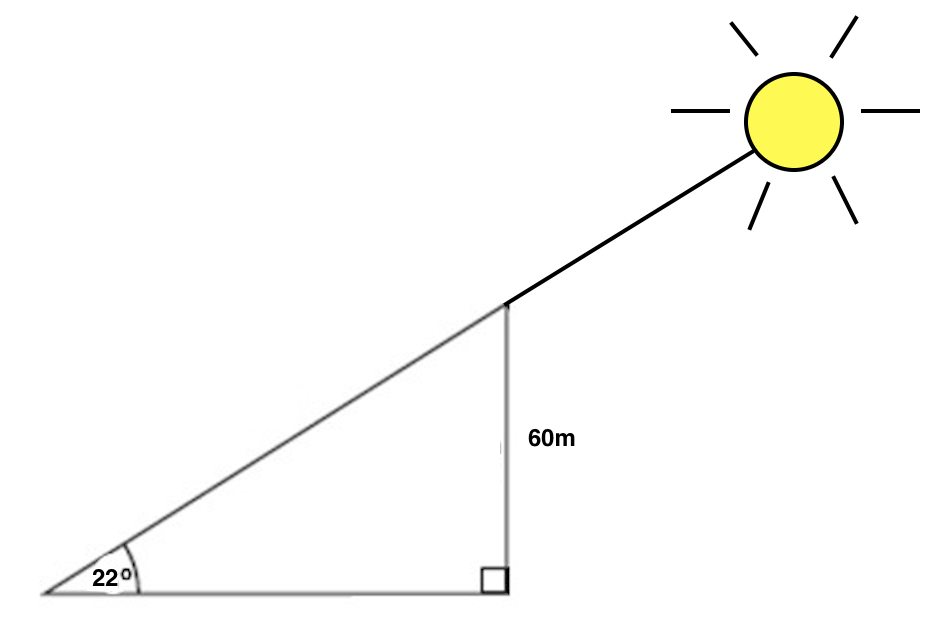
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.

Therefore the shadow cast by the building is 150 meters long.

If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)

Example Question #7 : Solving Word Problems With Trigonometry

From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19 o . How far from the boat is the top of the lighthouse?

423.18 meters

318.18 meters

36.15 meters

110.53 meters

To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.

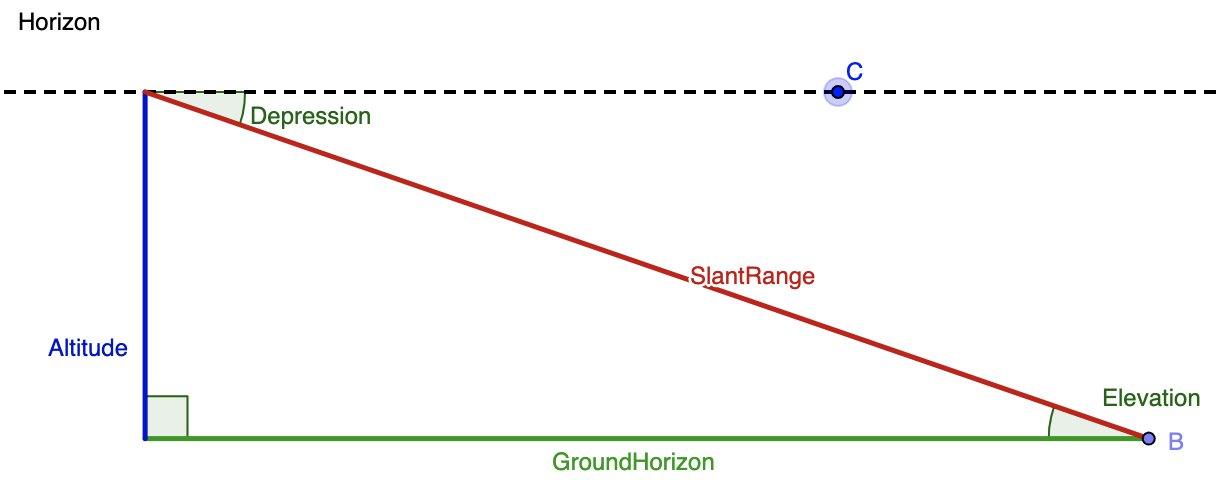
Merging together the given info and this diagram, we know that the angle of depression is 19 o  and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:

Example Question #8 : Solving Word Problems With Trigonometry

Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22 o to the horizontal, how high above her starting point is she when she arrives at the lookout?

9.37 meters

1480 meters

3708.74 meters

10677.87 meters

1616.1 meters

As with other trig problems, begin with a sketch of a diagram of the given and sought after information.

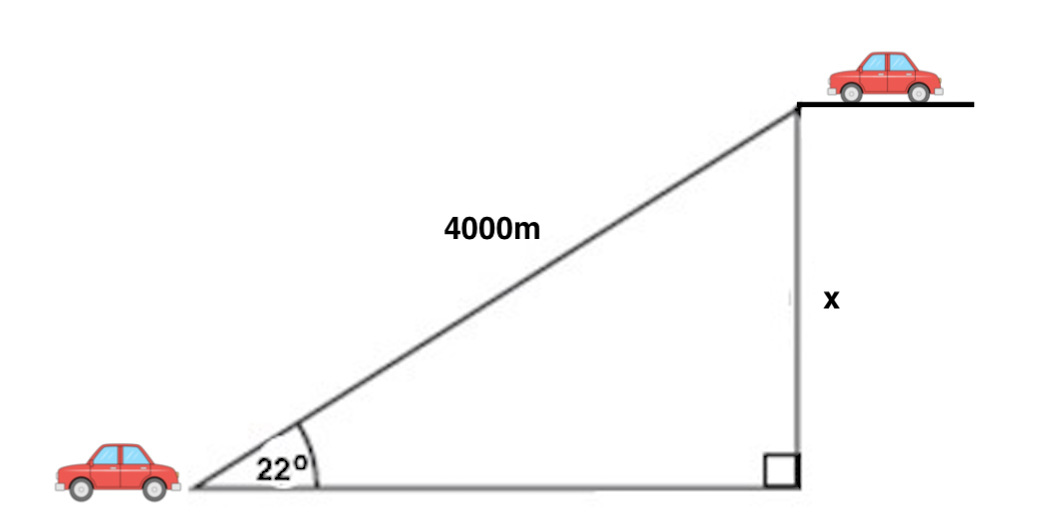
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22 o . Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:

Therefore the change in height between Angelina's starting and ending points is 1480 meters. 

Example Question #9 : Solving Word Problems With Trigonometry

Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48 o . How high is the taller building?

To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle. 

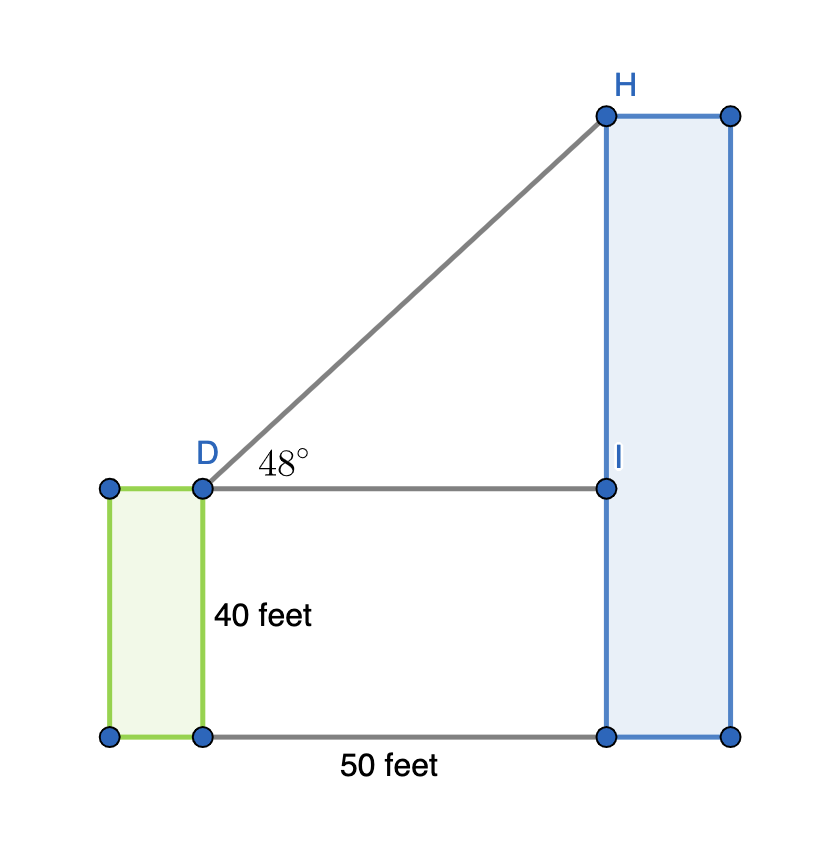
Example Question #10 : Solving Word Problems With Trigonometry

Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32 o . How high is the taller building?

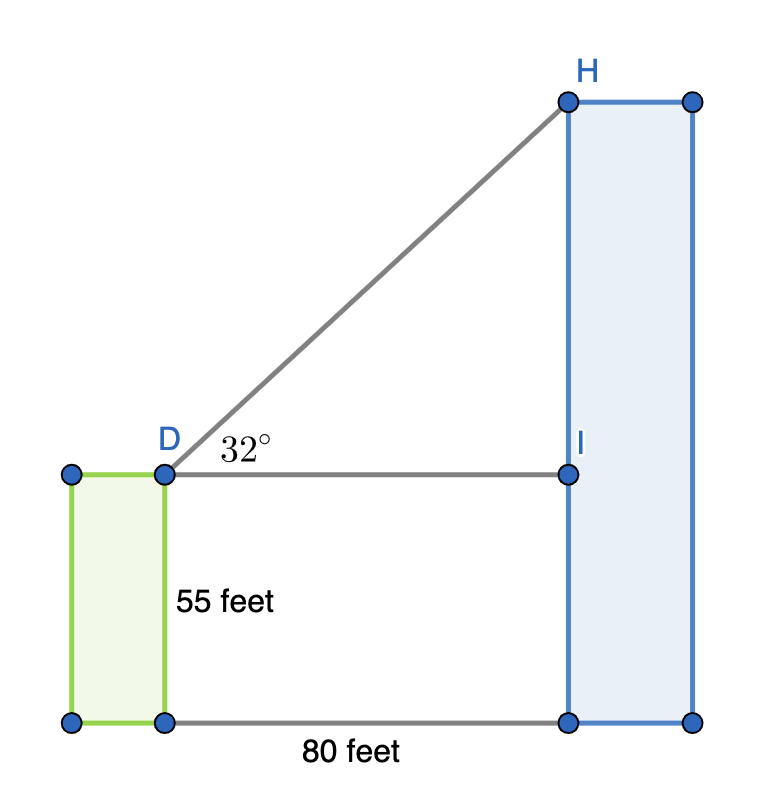
Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.