multiplication of integers problem solving

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

M and D Integers

Multiplying and dividing integers

Here you will learn strategies on how to multiply and divide integers, including using visual models as well as using the number line.

Students will first learn about integers in 6th grade math as part of their work with the number system and expand that knowledge to operations with integers in the 7th grade.

What are multiplying and dividing integers?

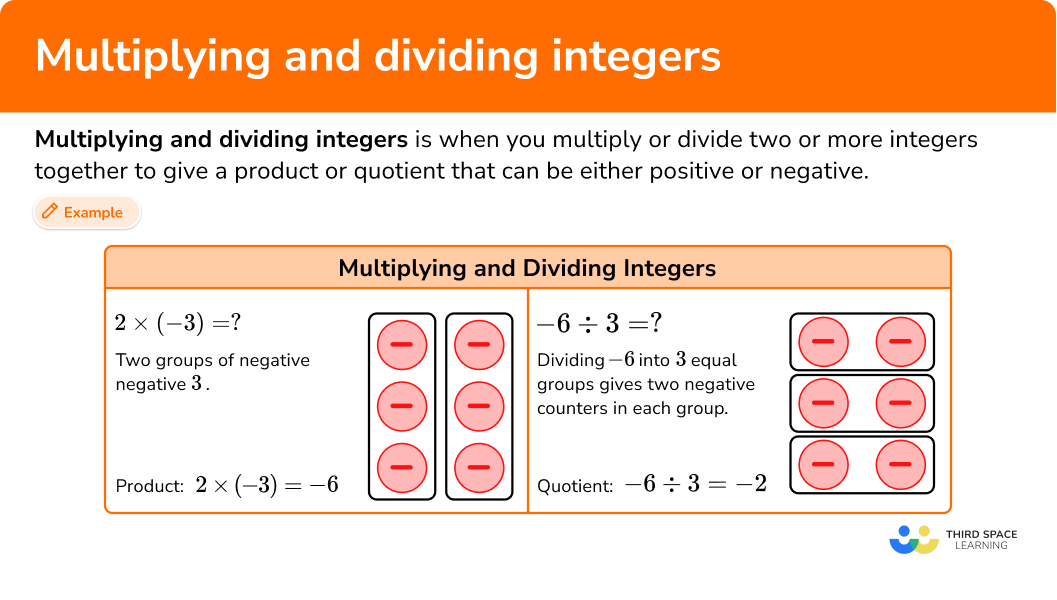
Multiplying and dividing integers is when you multiply or divide two or more integers together to give a product or quotient that can be either positive or negative.

You can multiply and divide integers using visual models or a rule.

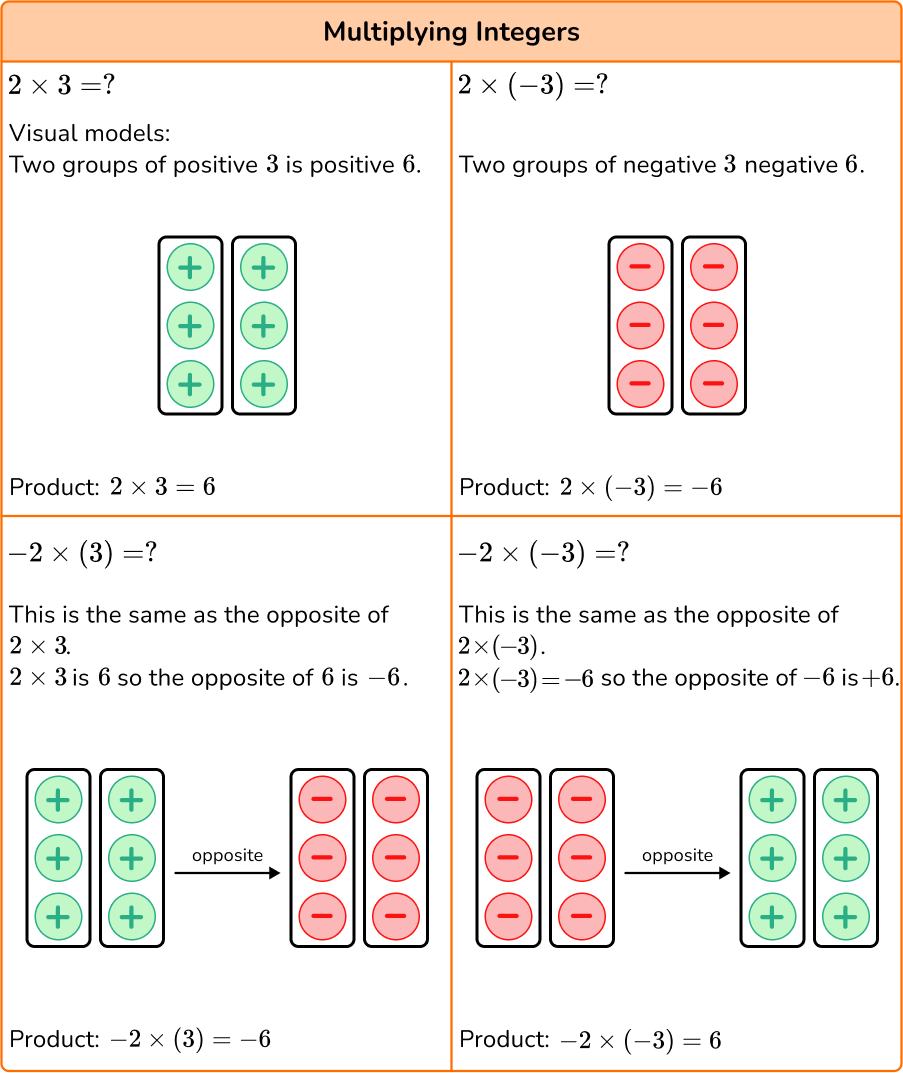
Do you notice a pattern or rule?

Rule for multiplying integers:

• If the integers have the same sign , the product will be positive .
• If the integers have different signs , the product will be negative .

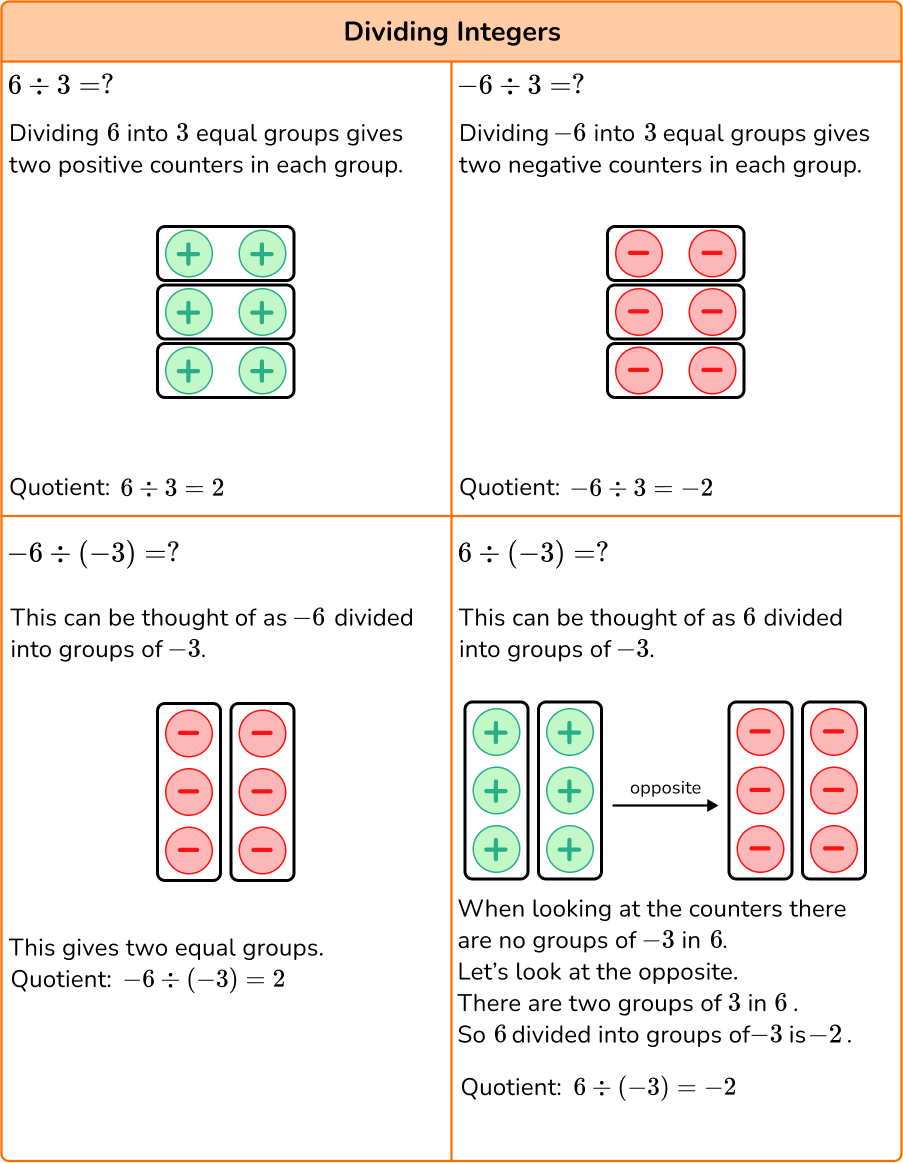
Rule for dividing integers:

• If the integers have the same sign , the quotient will be positive .
• If the integers have different signs , the quotient will be negative .

Common Core State Standards

How does this apply to 6th grade math and 7th grade math?

• Grade 6: Number System (6.NS.C.6) Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
• Grade 7: Number System (7.NS.A.2) Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.

[FREE] Multiplication and Division Check for Understanding (Grade 4, 5 and 7)

Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4, 5 and 7 grade multiplication and division topics to identify areas of strength and support!

How to multiply and divide integers?

In order to add and subtract integers using counters:

• If the integers have the same sign, the product or quotient is positive.  If not, go to step 2.

If the integers have different signs, the product or quotient is negative.

Find the product or quotient.

Multiplying and dividing integers examples

Example 1: multiplying integers with the same sign.

Multiply: (-4) \times(-12)= \, ?

• If the integers have the same sign, the product or quotient is positive. If they don’t go to step 2. 

-4 and -12 have the same sign so the product is positive.

2 If the integers have different signs, the product or quotient is negative.

Integers have the same sign.

3 Find the product or quotient.

(-4) \times(-12)=48

Example 2: multiplying integers with different signs

Multiply: (-13) \times 8= \, ?

If the integers have the same sign, the product or quotient is positive.  If not, go to step 2.

-13 and 8 do not have the same sign.

The integers have different signs so the product is negative.

Find the product or the quotient.

(-13) \times 8=-104

Example 3: dividing integers with the same sign

Divide: \cfrac{(-18)}{(-3)}= \, ?

-18 and -3 have the same sign so the quotient will be positive.

\cfrac{(-18)}{(-3)}=6

Example 4: dividing integers with different signs

Divide: -120 \div 3= \, ?

-120 and 3 do not have the same sign.

-120 and 3 have different signs so the quotient will be negative.

-120 \div 3=-40

Example 5: multiplying integers word problem

From sea level, a submarine descends 25 \, ft. per minute (-25 \, ft.).

After 6 minutes, the submarine’s distance can be modeled by (-25) \times 6 = \, d , where d is the submarine in relation to sea level.

How far below sea level is the submarine?

-25 and 6 do not have the same sign.

-25 and 6 have different signs so the product will be negative.

-25 \times 6=-150

Because the submarine is descending, after 6 minutes it will be 150 feet below sea level.

Example 6: dividing integer word problems

On a certain winter day, the temperature changed at a rate of -4 degrees Fahrenheit per hour.

After a specific amount of time, the change in temperature was -36 degrees Fahrenheit, which is modeled by (-36) \div (-4) = \, h, where h represents the amount of hours.

How long did it take for the change in temperature to be -36 degrees Fahrenheit?

-36 and -4 have the same sign so the quotient is positive.

The integers have the same sign.

(-36) \div(-4)=9

Teaching tips for multiplying and dividing integers

• Multiplying and dividing integers are foundational skills for Algebra 1. Using manipulatives helps students formulate conceptual understanding.
• Have students identify the patterns with multiplying and dividing integers so that they can figure out the rules on their own.
• Although practice integer worksheets have their place, have students practice problems through digital games or scavenger hunts around the room to make it engaging.
• Reinforce essential vocabulary such as dividend, divisor, quotient, factors,  and product.

Easy mistakes to make

• Mixing up the rules for multiplication and division For example, when multiplying integers with the same sign, you get a negative product, and when dividing integers with the same sign, you get a negative quotient.
• Mixing up the rules of multiplication and division with addition and subtraction For example, applying the rule of addition of integers to (15) \div(-3)=5 where the absolute value of 15 is greater than the absolute value of 3 so the answer must be positive.

Related multiplication and division lessons

This multiplying and dividing integers topic guide is part of our series on multiplication and division. You may find it helpful to start with the main multiplication and division topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:

• Multiplication and division
• Multiplying multi-digit numbers
• Understanding multiplication
• Multiplication and division within 100
• Long division
• Multiplying and dividing rational numbers
• Understanding division
• Dividing multi-digit numbers
• Multiplicative comparison

Practice multiplying and dividing integers

1. Multiply: (6) \times(-2)=\text { ? }

Using the rule for multiplying integers, 6 and -2 have different signs, so the product is negative.

(6) \times(-2)=-12

You can check your answer with counters.

6 groups of -2 counters is -12 counters

2. Multiply: (-15) \times(-3)= \text { ? }

Using the rule for multiplying integers, -15 and -3 have the same sign, so the product is positive.

(-15) \times(-3)=45

3. Divide: (-52) \div(4)= \text { ? }

Using the rule for dividing integers, -52 and 4 have different signs, so the quotient is negative.

(-52) \div(4)=-13

4. Divide: \cfrac{(-72)}{(-9)}= \text { ? }

Using the rule for dividing integers, -72 and -9 have the same sign, so the quotient is positive.

\cfrac{(-72)}{(-9)}=8

5. Multiply: (-190) \times(-10)= \text { ? }

Using the rule for multiplying integers, -190 and -10 have the same sign, so the product is positive.

(-190) \times(-10)=1900

6. A deep sea diver descends at a rate of 10 feet per minute below sea level. The diver descends at this rate for 8 minutes, which can be modeled by 8 \times (-10) = d, where d is how far the diver is below sea level. After 8 minutes, how far did the diver descend?

Using the rule, the signs of the numbers are different, so the product is negative.

8 \times(-10)=-80

The diver descended to -80 feet.

Multiplying and dividing integers FAQs

When it comes to sets of numbers, whole numbers are 0 and positive whole numbers. The set of integers includes all negative whole numbers, 0, and all positive whole numbers.

Multiplication and division of integers help when simplifying algebraic expressions and solving equations.

Yes, positive numbers are to the right of 0 and negative numbers are to the left of 0.

The positive sign does not necessarily need to be written in front of a number. For example, +5 is the same as 5. The positive sign is understood.

The next lessons are

• Types of numbers
• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

UP Class 6th

Course: up class 6th   >   unit 18.

• Multiplying positive & negative numbers
• Why a negative times a negative is a positive

Multiplication of integers

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Multiplying Integers

Videos, worksheets, songs and solutions to help Grade 6 students learn how to multiply integers.

In these lessons, we will learn how to use the rules for multiplying integers.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

Multiplication of integers

Download & Print Only $4.90

Multiplying with negative numbers

Practice integer worksheets on multiplying with negative numbers. Horizontal and vertical multiplication.

Horizontal:

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?

• Math Article
• Properties Multiplication Integers

Properties of Multiplication of Integers

The properties of multiplication of integers refer to the product of two or more integers. To recall, the set of numbers that consist of natural numbers, the additive inverse of natural numbers and zero are known as integers. Thus, integers can either be positive or negative, which is represented on a number line. They are usually represented by Z. The examples of integers are 1, 2, 3, 0, -10, -7, etc.

The four basic mathematical operations i.e. Addition, subtraction, multiplication, division and the properties related to these operations can be applied to integers as well.

The rules of the multiplication of integers are explained here in this article. To multiply any two integers, we should learn the basic properties of multiplication such as commutative property, associative property, etc. Learning these properties will help the students of Class 1 to 10, to solve multiplication problems easily.

Multiplication of Integers

Multiplication is basically the repeated addition of numbers. For example, if we say, 2 multiplied by 3, it means 2 is added to itself three times. 2 x 3 = 2 + 2 + 2 = 6

Therefore multiplication of integers is the repeated addition as:

Where a and n are both integers.

What are the Properties of Multiplication of Integers?

The properties of multiplication of integers are:

• Closure property
• Commutative property
• Associative property
• Distributive property

Multiplication by zero

• Multiplicative identity

Some of the properties of addition such as commutative and associative properties are also similar to those properties of multiplication. Thus, becomes easier to remember such properties.

Closure Property of Multiplication

According to this property, if two integers a and b are multiplied then their resultant a × b is also an integer. Therefore, integers are closed under multiplication.

a × b is an integer, for every integer a and b

• 2 x -1 = -2

Commutative Property of Multiplication

The commutative property of multiplication of integers states that altering the order of operands or the integers does not affect the result of the multiplication.

a × b = b × a, for every integer a and b

• 3 x 4 = 4 x 3 (=12)
• 5 x 2 = 2 x 5 (=10)

Associative Property of Multiplication

The result of the product of three or more integers is irrespective of the grouping of these integers. In general, if a, b and c are three integers then,

a × (b × c) = (a × b) × c

• 3 x (4 x 5) = (3 x 4) x 5 (=60)
• -2 x (-1 x -3) = (-2 x -1) x -3 (= -6)

Distributive Property of Multiplication

According to the distributive property of multiplication of integers, if a, b and c are three integers then,

a× (b + c) = (a × b) + (a × c)

• 2 x (2 + 3) = (2 x 2) + (2 x 3)
• 2 x 6 = 4 + 6

On multiplying any integer by zero the result is always zero. In general, if a and b are two integers then,

a × 0 = 0 × a = 0

• -10 x 0 = 0
• 100 x 0 = 0

Thus, we can see, any integer whether it is the smallest one or the largest one, when multiplied by zero, results in zero only.

Multiplicative Identity of Integers

On multiplying any integer by 1 the result obtained is the integer itself. In general, if a and b are two integers then,

a × 1 = 1 × a = a

Therefore 1 is the Multiplicative Identity of Integers.

• 23 x 1 = 23
• 44 x 1 = 44
• -79 x 1 = -79
• -105 x 1 = -105

Other Properties of Multiplication

1. If a, b and c are the integers and a > b, then; a x c > b x c

Example: If 5 > 4

5 x 2 > 4 x 2

2. Change of Sign Property.

• Multiplication of two positive integers is always positive.
• Multiplication of two negative integers is always positive.
• Multiplication of a positive integer and a negative integer results in a negative integer.
• (+2) x (+ 4) = +8
• (-2) x (-4) = +8
• (-2) x (+4) = -8

Related Articles

• Whole Numbers
• Natural Numbers
• Real Numbers
• Number System
• Arithmetic Operations

Solved Examples on Properties of Multiplication

Find the product using suitable properties.

Q.1. 26 x (-48) + (-48) x (-36).

Solution: Given, 26 x (-48) + (-48) x (-36)

On rearranging the given expression, using commutative property, we get;

⇒ (-48) x (26) + (-48) x (-36)

Again using distributive property, we get;

⇒ (-48) x (-10)

Q.2. (-25) x (101).

Solution: Given, (-25) x 101

We can write the above expression as:

⇒ (-25) x (100+1)

Using distributive property, we get;

⇒ (-25 x 100) + (-25 x 1)

⇒ -2500 + (-25)

⇒ -2500 – 25

Q.3. 4 x 23 x (-125).

Solution: Given, 4 x 23 x (-125)

Using associative property, we can arrange the given expression as:

⇒ 23 x 4 x (-125)

⇒ 23 x (-500)

Worksheet on Properties of Multiplication

Fill in the blanks:

• 8 x 5 = ___ x 8
• (1 x 2) x 9 = 1 x (2 x __)
• 10 x (10 + 10) = ___
• 100 x 0 = _____
• 121 x 1 = ____
• 9 x 10 = ____
• 3 x -8 = ____

Find the product of the following:

• 10 x 10 x 10 = ?
• 15 x 10 = ?

Which properties of multiplication are these?

• 2190 x 1 = 2190 ___________
• 3 x 100 = 100 x 3 __________
• (10 x 40) x 2 = 10 x (40 x 2) ______________
• 1200 x 0 = 0 ___________

Keep visiting BYJU’S and Subscribe to our YouTube channel for learning number systems and other mathematical topics in a fun and engaging way. Also, register now to get access to 1000+ hours of engaging video content.

Frequently Asked Questions on Properties of Multiplication

What are the six properties of the multiplication of integers, what is the associative property of multiplication, which equation shows the distributive property of multiplication, what is the commutative property of multiplication, what are the four major operations of integers.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

It is very helpfull

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Integer Word Problems Worksheets

An integer is defined as a number that can be written without a fractional component. For example, 11, 8, 0, and −1908 are integers whereas √5, Π are not integers. The set of integers consists of zero, the positive natural numbers, and their additive inverses. Integers are closed under the operations of addition and multiplication . Integer word problems worksheets provide a variety of word problems associated with the use and properties of integers. 

Benefits of Integers Word Problems Worksheets

We use integers in our day-to-day life like measuring temperature, sea level, and speed limit. Translating verbal descriptions into expressions is an essential initial step in solving word problems. Deposits are normally represented by a positive sign and withdrawals are denoted by a negative sign. Negative numbers are used in weather forecasting to show the temperature of a region. Solving these integers word problems will help us relate the concept with practical applications.

Download Integers Word Problems Worksheet PDFs

These math worksheets should be practiced regularly and are free to download in PDF formats.

☛ Check Grade wise Integers Word Problems Worksheets

• 6th Grade Integers Worksheets
• Integers Worksheets for Grade 7
• 8th Grade Integers Worksheets

Multiplication of integers Calculator

Get detailed solutions to your math problems with our multiplication of integers step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems, are you struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Related Calculators

• WordPress.org
• Documentation
• Learn WordPress
• Members Newsfeed

Activities to Teach Students to Multiply and Divide Integers

• Uncategorized

Teaching multiplication and division of integers can be quite tough, but it is an essential skill that every student needs to learn. Multiplication and division are two of the most important mathematical operations that students will encounter, and mastery of these skills is critical for success in math.

As an educator, it’s important to use a range of activities to help students learn multiplication and division of integers easily. Here are some tried and tested activities that can help teach students how to multiply and divide integers effectively.

1. Model Building

Model building is a hands-on activity that makes multiplication and division of integers accessible to students. Provide students with a set of colored cubes or blocks representing positive and negative integers. Ask them to build a model to demonstrate a multiplication or division problem. For instance, students can use blocks to represent −2 and 3, respectively, and count how many total blocks are in the model. The total number of blocks in the model will give the answer for the multiplication problem. Similarly, divide the total number of blocks into how many groups needed to make the model to get the answer for the division problem.

2. Number Line

Using a number line is an excellent tool that helps students visualize multiplication and division of integers. Select a couple of integers and ask the students to mark them on the number line. Next, create a problem by asking the students to multiply or divide those numbers. Ask them to skip count along the number line to get the solution. For example, suppose you ask the students to divide −8 by 2. They could start at −8 and count in steps of two until they reach zero on the number line. The number zero is the answer.

3. Real-Life Scenarios

It is helpful for students always to see how math relates to real-life scenarios. One way to do this is to provide students with real-life problems and scenarios where they can apply multiplication and division of integers. For example, you can create problems like “You have $-24 in your bank account, and you want to buy two 5-dollar items. How much overdrawn will you be?” Solving real-life scenarios that call for multiplication and division makes problem-solving fun and meaningful to them.

4. Collaborative Competition

Divide the class into teams, and provide each team with a set of integers and a set of multiplication and division problems. The objective of the game is to be the first team to solve the problems correctly and earn points. This game helps the students to collaborate, explain their reasoning, and solve problems collaboratively while having fun.

In conclusion, mastery of multiplication and division of integers is essential in developing strong mathematical foundations. By incorporating fun and engaging activities like model building, the number line, real-life scenarios, and collaborative competition into your teaching routine, you can help students truly understand and learn these complex concepts. These activities foster collaboration, critical thinking, communication, and problem-solving skills that will be valuable throughout their lifetime.

Your email address will not be published.

Related Articles

Introduction Canoeing is a versatile and engaging sport that combines physical activity,…

Introduction Education is the foundation upon which knowledge, skills, and values are…

Introduction The Lizzie Borden case is one of the most notorious unsolved…

Pedagogue is a social media network where educators can learn and grow. It's a safe space where they can share advice, strategies, tools, hacks, resources, etc., and work together to improve their teaching skills and the academic performance of the students in their charge.

If you want to collaborate with educators from around the globe, facilitate remote learning, etc., sign up for a free account today and start making connections.

Pedagogue is Free Now, and Free Forever!

• New? Start Here
• Frequently Asked Questions
• Privacy Policy
• Terms of Service
• Registration

Don't you have an account? Register Now! it's really simple and you can start enjoying all the benefits!

We just sent you an Email. Please Open it up to activate your account.

I allow this website to collect and store submitted data.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.1.4: Multiplication and Division of Integers

• Last updated
• Save as PDF
• Page ID 116756

• David Arnold
• College of the Redwoods

Before we begin, let it be known that the integers satisfy the same properties of multiplication as do the whole numbers.

Integer Properties of Multiplication

Commutative Property. If a and b are integers, then their product commutes. That is,

\[a \cdot b = b \cdot a.\nonumber \]

Associative Property. If a, b, and c are integers, then their product is associative. That is,

\[(a \cdot b) \cdot c = a \cdot (b \cdot c).\nonumber \]

Multiplicative Identity Property. If a is any integer, then

\[a \cdot 1 = a \text{ and } 1 \cdot a = a.\nonumber \]

Because multiplying any integer by 1 returns the identical integer, the integer 1 is called the multiplicative identity .

In Section 1.3, we learned that multiplication is equivalent to repeated addition . For example,

\[ 3 \cdot 4 = \underbrace{4 + 4 + 4}_{\text{three fours}} \nonumber \]

On the number line, three sets of four is equivalent to walking three sets of four units to the right, starting from zero, as shown in Figure \(\PageIndex{1}\).

This example and a little thought should convince readers that the product of two positive integers will always be a positive integer.

The Product of Two Positive Integers

If a and b are two positive integers, then their product ab is also a positive integer.

For example, 2 · 3 = 6 and 13 · 117 = 1521. In each case, the product of two positive integers is a positive integer.

The Product of a Positive Integer and a Negative Integer

If we continue with the idea that multiplication is equivalent to repeated addition, then it must be that

\[ 3 \cdot (-4) = \underbrace{-4+(-4)+(-4)}_{ \text{three negative fours}}. \nonumber\nonumber \]

Pictured on the number line, 3 · (−4) would then be equivalent to walking three sets of negative four units (to the left), starting from zero, as shown in Figure \(\PageIndex{2}\).

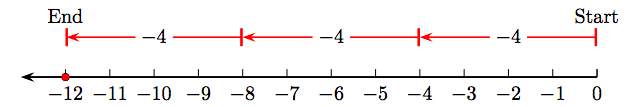
Note, at least in this particular case, that the product of a positive integer and a negative integer is a negative integer.

We’ve shown that 3 · (−4) = −12. However, integer multiplication is commutative, so it must also be true that −4 · 3 = −12. That is, the product of a negative integer and a positive integer is also a negative integer. Although not a proof, this argument motivates the following fact about integer multiplication.

Two facts are true:

• If a is a positive integer and b is a negative integer, then the product ab is a negative integer.
• If a is a negative integer and b is a positive integer, then the product ab is a negative integer.

Thus, for example, 5 ·(−12) = −60 and −13 · 2 = −26. In each case the answer is negative because we are taking a product where one of the factors is positive and the other is negative.

The Distributive Property

The integers satisfy the distributive property.

Let a , b , and c be integers. Then,

\[a \cdot (b + c) = a \cdot b + a \cdot c.\nonumber \]

We say that “multiplication is distributive with respect to addition.”

Note how the a is “distributed.” The a is multiplied times each term in the parentheses.

For example, consider the expression 3 · (4 + 5). We can evaluate this expression according to the order of operations, simplifying the expression inside the parentheses first.

\[ \begin{align*} 3 \cdot (4 + 5) &= 3 \cdot 9 \\[4pt] &= 27 \end{align*}\nonumber \]

But we can also use the distributive property, multiplying each term inside the parentheses by three, then simplifying the result.

\[ \begin{aligned} ~ & \textcolor{red}{ \text{ Distribute the 3: }} 3 (4+5)   \\ ~ & \textcolor{red}{ \text{ Perform multiplications first:}}= 3 \cdot 4 + 3 \cdot 5  \\ ~ & \textcolor{red}{ \text{ Add:}}=12+15  \\ ~ & \textcolor{red}{ \text{ Sum:}}=27  \\  \end{aligned}\nonumber \]

Note that evaluating 3 · (4 + 5) using the distributive property provides the same result as the evaluation (2.1) using the order of operations.

The Multiplicative Property of Zero

The distributive property can be used to provide proofs of a number of important properties of integers. One important property is the fact that if you multiply an integer by zero, the product is zero. Here is a proof of that fact that uses the distributive property.

Let a be any integer. Then,

\[ \begin{aligned} a \cdot 0 = a \cdot (0 + 0) ~ & \textcolor{red}{ \text{ Additive Identity Property: = 0 + 0 = 0.}} \\ a \cdot 0 = a \cdot 0 + a \cdot 0 ~ & \textcolor{red}{ \text{ Distribute } a \text{ times each zero in the parentheses.}} \end{aligned}\nonumber \]

Next, to “undo” the effect of adding a · 0, subtract a · 0 from both sides of the equation.

\[ \begin{aligned} a \cdot 0 - a \cdot 0 = a \cdot 0 + a \cdot 0 + a \cdot 0 - a \cdot 0 ~ & \textcolor{red}{ \text{ Subtract } a \cdot 0 \text{ from both sides.}} \\ 0 = a \cdot 0 ~ & \textcolor{red}{ a \cdot 0 - a \cdot 0 = 0 \text{ on each side.}} \end{aligned}\nonumber \]

Multiplicative Property of Zero

Let a represent any integer. Then

a · 0 = 0 and 0 · a = 0.

Thus, for example, −18 · 0 = 0 and 0 · 122 = 0.

Multiplying by Minus One

Here is another useful application of the distributive property.

\[ \begin{aligned}   (-1) a + a = (-1)a + 1a  ~ & \textcolor{red}{ \text{ Replace } a \text{ with } 1a.} \\  = (-1 + 1)a ~ & \textcolor{red}{ \text{ Use the distributive property to factor out } a.} \\ =0a  ~ & \textcolor{red}{ \text{ Replace } -1+1 \text{ with } 0.} \\ =0~ & \textcolor{red}{ \text{ Replace } 0a \text{ with 0.}} \end{aligned}\nonumber \]

Thus, (−1) a + a = 0. That is, if you add (−1) a to a you get zero. However, the Additive Inverse Property says that − a is the unique number that you add to a to get zero. The conclusion must be that (−1) a = − a .

If a is any integer, then

\[(−1)a = −a.\nonumber \]

Thus, for example, −1(4) = −4 and −1(−4) = −(−4) = 4.

This property is rather important, as we will see in future work. Not only does it tell us that (−1) a = − a , but it also tells us that if we see − a , then it can be interpreted to mean (−1) a .

The Product of Two Negative Integers

We can employ the multiplicative property of −1, that is, (−1) a = − a to find the product of two negative numbers.

\[ \begin{aligned} (-4)(-3) = [(-1)(4)](-3) ~ & \textcolor{red}{ \text{ Replace } -4 \text{ with } (-1)(4).} \\ =(-1)[(4)(-3)] ~ & \textcolor{red}{ \text{ Use the associative property to regroup.}} \\ = (-1)(-12) ~ & \textcolor{red}{ \text{ We know: } (4)(-3) = -12.} \\ = -(-12) ~ & \textcolor{red}{ (-1)a = -a. \text{ Here } (-1)(-12) = -(-12).} \\ =12 ~ & \textcolor{red}{ -(-a) = a. \text{ Here } -(-12) = 12.} \end{aligned}\nonumber \]

Thus, at least in the case of (−4)(−3), the product of two negative integers is a positive integer. This is true in general.

If both a and b are negative integers, then their product ab is a positive integer.

Thus, for example, (−5)(−7) = 35 and (−112)(−6) = 672. In each case the answer is positive, because the product of two negative integers is a positive integer.

Memory Device

Here’s a simple memory device to help remember the rules for finding the product of two integers.

Like and Unlike Signs

There are two cases:

Unlike Signs . The product of two integers with unlike signs is negative. That is:

(+)(−) = −

(−)(+) = −

Like Signs . The product of two integers with like signs is positive. That is:

(−)(−)=+

Simplify: (a) (−3)(−2), (b) (4)(−10), and (c) (12)(−3).

In each example, we use the “like” and “unlike” signs approach.

a) Like signs gives a positive result. Hence, (−3)(−2) = 6.

b) Unlike signs gives a negative result. Hence, (4)(−10) = −40.

c) Unlike signs gives a negative result. Hence, (12)(−3) = −36.

Simplify: (a) (−12)(4) and (b) (−3)(−11).

(a) −48, (b) 33

Simplify (−3)(2)(−4)(−2).

Order of operations demands that we work from left to right.

\[ \begin{aligned} (-3)(2)(-4)(-2) = (-6)(-4)(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-3)(2) = -6.} \\ = (24)(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-6)(-4) = 24.} \\ =-48 ~ & \textcolor{red}{ \text{ Multiply: } (24)(-2) = -48.} \end{aligned}\nonumber \]

Hence, (−3)(2)(−4)(−2) = −48.

Simplify: (−2)(−3)(4)(−1).

Simplify: (a)(−2) 3 and (c) (−3) 4 .

In each example, use

\[ a^m = \underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_{m \text{ times}},\nonumber \]

then work left to right with the multiplication.

a) Use the definition of an exponent, then order of operations.

\[ \begin{aligned} (-2)^3 = (-2)(-2)(-2) ~ & \textcolor{red}{ \text{ Write } -2 \text{ as a factor three times.}} \\ =4(-2) ~ & \textcolor{red}{ \text{ Work left to right: } (-2)(-2) = 4.} \\ =-8 \end{aligned}\nonumber \]

b) Use the definition of an exponent, then order of operations.

\[ \begin{aligned} (-3)^4 = (-3)(-3)(-3)(-3) ~ & \textcolor{red}{ \text{ Write } -3 \text{ as a factor four times.}} \\ =9(-3)(-3) ~ & \textcolor{red}{ \text{ Work left to right: } (-3)(-3) = 9.} \\ =-27(-3) ~ & \textcolor{red}{ \text{ Work left to right: } 9(-3) = -27.} \\ = 81 \end{aligned}\nonumber \]

Simplify: (a) (−2) 2 and (b) −2 2 .

(a) 4 and (b) −4

Example 3 motivates the following fact.

Even and Odd

Two facts are apparent.

• If a product contains an odd number of negative factors, then the product is negative.
• If a product contains an even number of negative factors, then the product is positive.

Thus, for example,

\[(−2)^5 = (−2)(−2)(−2)(−2)(−2) = −32\nonumber \]

quickly evaluates as −32 as it has an odd number of negative factors. On the other hand,

\[(−2)^6 = (−2)(−2)(−2)(−2)(−2)(−2) = 64\nonumber \]

quickly evaluates as 64 as it has an even number of negative factors.

Division of Integers

Consider that

\(\frac{12}{3} = 4\) because \(3(4) = 12\) and \(\frac{-12}{-3} = 4\) because \(-3(4) = -12\).

In like manner,

\(\frac{12}{-3} = -4\) because -3(-4) = 12 and \(\frac{-12}{3} = -4\) because \(3(-4) = -12\).

Thus, the rules for dividing integers are the same as the rules for multiplying integers.

Unlike Signs. The quotient of two integers with unlike signs is negative. That is,

\[ \begin{array} \frac{(+)}{(-)} = - \\ \frac{(-)}{(+)} = - \end{array}\nonumber \]

Like Signs. The quotient of two integers with like signs is positive. That is,

\[ \begin{array} \frac{(+)}{(+)} = + \\ \frac{(-)}{(-)} = + \end{array}\nonumber \]

Thus, for example, 12/(−6) = −2 and −44/(−4) = 11. In the first case, unlike signs gives a negative quotient. In the second case, like signs gives a positive quotient.

One final reminder.

Division by Zero is Undefined

If a is any integer, the quotient

\[ \frac{a}{0}\nonumber \]

is undefined. Division by zero is meaningless.

See the discussion in Section 1.3 for a discussion on division by zero.

Simplify: (a) −12/(−4), (b) 6/(−3), and (c) −15/0.

a) Like signs gives a positive result. Hence,

\[ \frac{-12}{-4} = 3.\nonumber \]

b) Unlike signs gives a negative result. Hence,

\[ \frac{6}{-3} = -2.\nonumber \]

c) Division by zero is undefined. Hence,

\[ \frac{-15}{0}\nonumber \]

is undefined.

Simplify: (a) −24/4 and (b) −28/(−7).

(a) −6, (b) 4

In Exercises 1-16, state the property of multiplication depicted by the given identity.

1. (−2) (−16)(13) = (−2)(−16) (13)

2. (10) (−15)(−6) = (10)(−15) (−6)

3. (−17)(−10) = (−10)(−17)

4. (−5)(3) = (3)(−5)

5. (4)(11) = (11)(4)

6. (−5)(−11) = (−11)(−5)

7. 16 · (8 + (−15) = 16 · 8 + 16 · (−15)

8. 1 · (−16 + (−6) = 1 · (−16) + 1 · (−6)

9. (17) (20)(11) = (17)(20) (11)

10. (14) (−20)(−18) = (14)(−20) (−18)

11. −19 · 1 = −19

12. −17 · 1 = −17

13. 8 · 1=8

14. −20 · 1 = −20

15. 14 · (−12 + 7 = 14 · (−12) + 14 · 7

16. −14 · (−3+6 = −14 · (−3) + (−14) · 6

In Exercises 17-36, simplify each given expression.

17. 4 · 7

18. 4 · 2

19. 3 · (−3)

20. 7 · (−9)

21. −1 · 10

22. −1 · 11

23. −1 · 0

24. −8 · 0

25. −1 · (−14)

26. −1 · (−13)

27. −1 · (−19)

28. −1 · (−17)

29. 2 · 0

30. −6 · 0

31. −3 · 8

32. 7 · (−3)

33. 7 · 9

34. 6 · 3

35. −1 · 5

36. −1 · 2

In Exercises 37-48, simplify each given expression.

37. (−7)(−1)(3)

38. (10)(6)(3)

39. (−7)(9)(10)(−10)

40. (−8)(−5)(7)(−9)

41. (6)(5)(8)

42. (7)(−1)(−9)

43. (−10)(4)(−3)(8)

44. (8)(−2)(−5)(2)

45. (6)(−3)(−8)

46. (−5)(−4)(1)

47. (2)(1)(3)(4)

48. (7)(5)(1)(4)

In Exercises 49-60, compute the exact value.

49. (−4) 4

50. (−3) 4

51. (−5) 4

52. (−2) 2

53. (−5) 2

54. (−3) 3

55. (−6) 2

56. (−6) 4

57. (−4) 5

58. (−4) 2

59. (−5) 3

60. (−3) 2

In Exercises 61-84, simplify each given expression.

61. −16 ÷ (−8)

62. −33 ÷ (−3)

63. \( \frac{-8}{1}\)

64. \(\frac{40}{-20}\)

65. \(\frac{-1}{0}\)

66. \(\frac{2}{0}\

67. −3 ÷ 3

68. −58 ÷ 29

69. \(\frac{56}{-28}\)

70. \(\frac{60}{-12}\)

71. 0 ÷ 15

72. 0 ÷ (−4)

73. \(\frac{63}{21}\)

74. \(\frac{-6}{-1}\)

75. \(\frac{78}{13}\)

76. \(\frac{-84}{-14}\)

77. 0 ÷ 5

78. 0 ÷ (−16)

79. \(\frac{17}{0}\)

80. \(\frac{-20}{0}\)

81. −45 ÷ 15

82. −28 ÷ 28

83. 12 ÷ 3

84. −22 ÷ (−22)

85. Scuba . A diver goes down 25 feet. A second diver then dives down 5 times further than the first diver. Write the final depth of the second diver as an integer.

86. Investing Loss . An investing club of five friends has lost $4400 on a trade. If they share the loss equally, write each members’ loss as an integer.

1. Associative property of multiplication

3. Commutative property of multiplication

5. Commutative property of multiplication

7. Distributive property

9. Associative property of multiplication

11. Multiplicative identity property

13. Multiplicative identity property

15. Distributive property

19. −9

21. −10

31. −24

35. −5

57. −1024

59. −125

63. −8

65. Division by zero is undefined.

67. −1

69. −2

79. Division by zero is undefined.

81. −3 83. 4

85. −125 feet