hypothesis for anova example

Hypothesis Testing - Analysis of Variance (ANOVA)

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific test considered here is called analysis of variance (ANOVA) and is a test of hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups. For example, in some clinical trials there are more than two comparison groups. In a clinical trial to evaluate a new medication for asthma, investigators might compare an experimental medication to a placebo and to a standard treatment (i.e., a medication currently being used). In an observational study such as the Framingham Heart Study, it might be of interest to compare mean blood pressure or mean cholesterol levels in persons who are underweight, normal weight, overweight and obese.  

The technique to test for a difference in more than two independent means is an extension of the two independent samples procedure discussed previously which applies when there are exactly two independent comparison groups. The ANOVA technique applies when there are two or more than two independent groups. The ANOVA procedure is used to compare the means of the comparison groups and is conducted using the same five step approach used in the scenarios discussed in previous sections. Because there are more than two groups, however, the computation of the test statistic is more involved. The test statistic must take into account the sample sizes, sample means and sample standard deviations in each of the comparison groups.

If one is examining the means observed among, say three groups, it might be tempting to perform three separate group to group comparisons, but this approach is incorrect because each of these comparisons fails to take into account the total data, and it increases the likelihood of incorrectly concluding that there are statistically significate differences, since each comparison adds to the probability of a type I error. Analysis of variance avoids these problemss by asking a more global question, i.e., whether there are significant differences among the groups, without addressing differences between any two groups in particular (although there are additional tests that can do this if the analysis of variance indicates that there are differences among the groups).

The fundamental strategy of ANOVA is to systematically examine variability within groups being compared and also examine variability among the groups being compared.

Learning Objectives

After completing this module, the student will be able to:

• Perform analysis of variance by hand
• Appropriately interpret results of analysis of variance tests
• Distinguish between one and two factor analysis of variance tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

The ANOVA Approach

Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:

The hypotheses of interest in an ANOVA are as follows:

• H 0 : μ 1 = μ 2 = μ 3 ... = μ k
• H 1 : Means are not all equal.

where k = the number of independent comparison groups.

In this example, the hypotheses are:

• H 0 : μ 1 = μ 2 = μ 3 = μ 4
• H 1 : The means are not all equal.

The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.

Test Statistic for ANOVA

The test statistic for testing H 0 : μ 1 = μ 2 = ... =   μ k is:

and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.

NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.

The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).  

The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:

df 1 = k-1 and df 2 =N-k,

where k is the number of comparison groups and N is the total number of observations in the analysis.   If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.

Rejection Region for F   Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.

The ANOVA Procedure

We will next illustrate the ANOVA procedure using the five step approach. Because the computation of the test statistic is involved, the computations are often organized in an ANOVA table. The ANOVA table breaks down the components of variation in the data into variation between treatments and error or residual variation. Statistical computing packages also produce ANOVA tables as part of their standard output for ANOVA, and the ANOVA table is set up as follows: 

where  

• X = individual observation,
• k = the number of treatments or independent comparison groups, and
• N = total number of observations or total sample size.

The ANOVA table above is organized as follows.

• The first column is entitled "Source of Variation" and delineates the between treatment and error or residual variation. The total variation is the sum of the between treatment and error variation.
• The second column is entitled "Sums of Squares (SS)" . The between treatment sums of squares is

and is computed by summing the squared differences between each treatment (or group) mean and the overall mean. The squared differences are weighted by the sample sizes per group (n j ). The error sums of squares is:

and is computed by summing the squared differences between each observation and its group mean (i.e., the squared differences between each observation in group 1 and the group 1 mean, the squared differences between each observation in group 2 and the group 2 mean, and so on). The double summation ( SS ) indicates summation of the squared differences within each treatment and then summation of these totals across treatments to produce a single value. (This will be illustrated in the following examples). The total sums of squares is:

and is computed by summing the squared differences between each observation and the overall sample mean. In an ANOVA, data are organized by comparison or treatment groups. If all of the data were pooled into a single sample, SST would reflect the numerator of the sample variance computed on the pooled or total sample. SST does not figure into the F statistic directly. However, SST = SSB + SSE, thus if two sums of squares are known, the third can be computed from the other two.

• The third column contains degrees of freedom . The between treatment degrees of freedom is df 1 = k-1. The error degrees of freedom is df 2 = N - k. The total degrees of freedom is N-1 (and it is also true that (k-1) + (N-k) = N-1).
• The fourth column contains "Mean Squares (MS)" which are computed by dividing sums of squares (SS) by degrees of freedom (df), row by row. Specifically, MSB=SSB/(k-1) and MSE=SSE/(N-k). Dividing SST/(N-1) produces the variance of the total sample. The F statistic is in the rightmost column of the ANOVA table and is computed by taking the ratio of MSB/MSE.  

A clinical trial is run to compare weight loss programs and participants are randomly assigned to one of the comparison programs and are counseled on the details of the assigned program. Participants follow the assigned program for 8 weeks. The outcome of interest is weight loss, defined as the difference in weight measured at the start of the study (baseline) and weight measured at the end of the study (8 weeks), measured in pounds.  

Three popular weight loss programs are considered. The first is a low calorie diet. The second is a low fat diet and the third is a low carbohydrate diet. For comparison purposes, a fourth group is considered as a control group. Participants in the fourth group are told that they are participating in a study of healthy behaviors with weight loss only one component of interest. The control group is included here to assess the placebo effect (i.e., weight loss due to simply participating in the study). A total of twenty patients agree to participate in the study and are randomly assigned to one of the four diet groups. Weights are measured at baseline and patients are counseled on the proper implementation of the assigned diet (with the exception of the control group). After 8 weeks, each patient's weight is again measured and the difference in weights is computed by subtracting the 8 week weight from the baseline weight. Positive differences indicate weight losses and negative differences indicate weight gains. For interpretation purposes, we refer to the differences in weights as weight losses and the observed weight losses are shown below.

Is there a statistically significant difference in the mean weight loss among the four diets?  We will run the ANOVA using the five-step approach.

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ 1 = μ 2 = μ 3 = μ 4 H 1 : Means are not all equal              α=0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is the F statistic for ANOVA, F=MSB/MSE.

• Step 3. Set up decision rule.  

The appropriate critical value can be found in a table of probabilities for the F distribution(see "Other Resources"). In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k. In this example, df 1 =k-1=4-1=3 and df 2 =N-k=20-4=16. The critical value is 3.24 and the decision rule is as follows: Reject H 0 if F > 3.24.

• Step 4. Compute the test statistic.  

To organize our computations we complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean based on the total sample.  

We can now compute

So, in this case:

Next we compute,

SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants in the low calorie diet:  

For the participants in the low fat diet:  

For the participants in the low carbohydrate diet:  

For the participants in the control group:

We can now construct the ANOVA table .

• Step 5. Conclusion.  

We reject H 0 because 8.43 > 3.24. We have statistically significant evidence at α=0.05 to show that there is a difference in mean weight loss among the four diets.    

ANOVA is a test that provides a global assessment of a statistical difference in more than two independent means. In this example, we find that there is a statistically significant difference in mean weight loss among the four diets considered. In addition to reporting the results of the statistical test of hypothesis (i.e., that there is a statistically significant difference in mean weight losses at α=0.05), investigators should also report the observed sample means to facilitate interpretation of the results. In this example, participants in the low calorie diet lost an average of 6.6 pounds over 8 weeks, as compared to 3.0 and 3.4 pounds in the low fat and low carbohydrate groups, respectively. Participants in the control group lost an average of 1.2 pounds which could be called the placebo effect because these participants were not participating in an active arm of the trial specifically targeted for weight loss. Are the observed weight losses clinically meaningful?

Another ANOVA Example

Calcium is an essential mineral that regulates the heart, is important for blood clotting and for building healthy bones. The National Osteoporosis Foundation recommends a daily calcium intake of 1000-1200 mg/day for adult men and women. While calcium is contained in some foods, most adults do not get enough calcium in their diets and take supplements. Unfortunately some of the supplements have side effects such as gastric distress, making them difficult for some patients to take on a regular basis.  

 A study is designed to test whether there is a difference in mean daily calcium intake in adults with normal bone density, adults with osteopenia (a low bone density which may lead to osteoporosis) and adults with osteoporosis. Adults 60 years of age with normal bone density, osteopenia and osteoporosis are selected at random from hospital records and invited to participate in the study. Each participant's daily calcium intake is measured based on reported food intake and supplements. The data are shown below.   

Is there a statistically significant difference in mean calcium intake in patients with normal bone density as compared to patients with osteopenia and osteoporosis? We will run the ANOVA using the five-step approach.

H 0 : μ 1 = μ 2 = μ 3 H 1 : Means are not all equal                            α=0.05

In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k.   In this example, df 1 =k-1=3-1=2 and df 2 =N-k=18-3=15. The critical value is 3.68 and the decision rule is as follows: Reject H 0 if F > 3.68.

To organize our computations we will complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean.  

 If we pool all N=18 observations, the overall mean is 817.8.

We can now compute:

Substituting:

SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants with normal bone density:

For participants with osteopenia:

For participants with osteoporosis:

We do not reject H 0 because 1.395 < 3.68. We do not have statistically significant evidence at a =0.05 to show that there is a difference in mean calcium intake in patients with normal bone density as compared to osteopenia and osterporosis. Are the differences in mean calcium intake clinically meaningful? If so, what might account for the lack of statistical significance?

One-Way ANOVA in R

The video below by Mike Marin demonstrates how to perform analysis of variance in R. It also covers some other statistical issues, but the initial part of the video will be useful to you.

Two-Factor ANOVA

The ANOVA tests described above are called one-factor ANOVAs. There is one treatment or grouping factor with k > 2 levels and we wish to compare the means across the different categories of this factor. The factor might represent different diets, different classifications of risk for disease (e.g., osteoporosis), different medical treatments, different age groups, or different racial/ethnic groups. There are situations where it may be of interest to compare means of a continuous outcome across two or more factors. For example, suppose a clinical trial is designed to compare five different treatments for joint pain in patients with osteoarthritis. Investigators might also hypothesize that there are differences in the outcome by sex. This is an example of a two-factor ANOVA where the factors are treatment (with 5 levels) and sex (with 2 levels). In the two-factor ANOVA, investigators can assess whether there are differences in means due to the treatment, by sex or whether there is a difference in outcomes by the combination or interaction of treatment and sex. Higher order ANOVAs are conducted in the same way as one-factor ANOVAs presented here and the computations are again organized in ANOVA tables with more rows to distinguish the different sources of variation (e.g., between treatments, between men and women). The following example illustrates the approach.

Consider the clinical trial outlined above in which three competing treatments for joint pain are compared in terms of their mean time to pain relief in patients with osteoarthritis. Because investigators hypothesize that there may be a difference in time to pain relief in men versus women, they randomly assign 15 participating men to one of the three competing treatments and randomly assign 15 participating women to one of the three competing treatments (i.e., stratified randomization). Participating men and women do not know to which treatment they are assigned. They are instructed to take the assigned medication when they experience joint pain and to record the time, in minutes, until the pain subsides. The data (times to pain relief) are shown below and are organized by the assigned treatment and sex of the participant.

Table of Time to Pain Relief by Treatment and Sex

The analysis in two-factor ANOVA is similar to that illustrated above for one-factor ANOVA. The computations are again organized in an ANOVA table, but the total variation is partitioned into that due to the main effect of treatment, the main effect of sex and the interaction effect. The results of the analysis are shown below (and were generated with a statistical computing package - here we focus on interpretation). 

 ANOVA Table for Two-Factor ANOVA

There are 4 statistical tests in the ANOVA table above. The first test is an overall test to assess whether there is a difference among the 6 cell means (cells are defined by treatment and sex). The F statistic is 20.7 and is highly statistically significant with p=0.0001. When the overall test is significant, focus then turns to the factors that may be driving the significance (in this example, treatment, sex or the interaction between the two). The next three statistical tests assess the significance of the main effect of treatment, the main effect of sex and the interaction effect. In this example, there is a highly significant main effect of treatment (p=0.0001) and a highly significant main effect of sex (p=0.0001). The interaction between the two does not reach statistical significance (p=0.91). The table below contains the mean times to pain relief in each of the treatments for men and women (Note that each sample mean is computed on the 5 observations measured under that experimental condition).  

Mean Time to Pain Relief by Treatment and Gender

Treatment A appears to be the most efficacious treatment for both men and women. The mean times to relief are lower in Treatment A for both men and women and highest in Treatment C for both men and women. Across all treatments, women report longer times to pain relief (See below).  

Notice that there is the same pattern of time to pain relief across treatments in both men and women (treatment effect). There is also a sex effect - specifically, time to pain relief is longer in women in every treatment.  

Suppose that the same clinical trial is replicated in a second clinical site and the following data are observed.

Table - Time to Pain Relief by Treatment and Sex - Clinical Site 2

The ANOVA table for the data measured in clinical site 2 is shown below.

Table - Summary of Two-Factor ANOVA - Clinical Site 2

Notice that the overall test is significant (F=19.4, p=0.0001), there is a significant treatment effect, sex effect and a highly significant interaction effect. The table below contains the mean times to relief in each of the treatments for men and women.  

Table - Mean Time to Pain Relief by Treatment and Gender - Clinical Site 2

Notice that now the differences in mean time to pain relief among the treatments depend on sex. Among men, the mean time to pain relief is highest in Treatment A and lowest in Treatment C. Among women, the reverse is true. This is an interaction effect (see below).  

Notice above that the treatment effect varies depending on sex. Thus, we cannot summarize an overall treatment effect (in men, treatment C is best, in women, treatment A is best).    

When interaction effects are present, some investigators do not examine main effects (i.e., do not test for treatment effect because the effect of treatment depends on sex). This issue is complex and is discussed in more detail in a later module. 

• Privacy Policy

Home » ANOVA (Analysis of variance) – Formulas, Types, and Examples

ANOVA (Analysis of variance) – Formulas, Types, and Examples

Table of Contents

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It is similar to the t-test, but the t-test is generally used for comparing two means, while ANOVA is used when you have more than two means to compare.

ANOVA is based on comparing the variance (or variation) between the data samples to the variation within each particular sample. If the between-group variance is high and the within-group variance is low, this provides evidence that the means of the groups are significantly different.

ANOVA Terminology

When discussing ANOVA, there are several key terms to understand:

• Factor : This is another term for the independent variable in your analysis. In a one-way ANOVA, there is one factor, while in a two-way ANOVA, there are two factors.
• Levels : These are the different groups or categories within a factor. For example, if the factor is ‘diet’ the levels might be ‘low fat’, ‘medium fat’, and ‘high fat’.
• Response Variable : This is the dependent variable or the outcome that you are measuring.
• Within-group Variance : This is the variance or spread of scores within each level of your factor.
• Between-group Variance : This is the variance or spread of scores between the different levels of your factor.
• Grand Mean : This is the overall mean when you consider all the data together, regardless of the factor level.
• Treatment Sums of Squares (SS) : This represents the between-group variability. It is the sum of the squared differences between the group means and the grand mean.
• Error Sums of Squares (SS) : This represents the within-group variability. It’s the sum of the squared differences between each observation and its group mean.
• Total Sums of Squares (SS) : This is the sum of the Treatment SS and the Error SS. It represents the total variability in the data.
• Degrees of Freedom (df) : The degrees of freedom are the number of values that have the freedom to vary when computing a statistic. For example, if you have ‘n’ observations in one group, then the degrees of freedom for that group is ‘n-1’.
• Mean Square (MS) : Mean Square is the average squared deviation and is calculated by dividing the sum of squares by the corresponding degrees of freedom.
• F-Ratio : This is the test statistic for ANOVAs, and it’s the ratio of the between-group variance to the within-group variance. If the between-group variance is significantly larger than the within-group variance, the F-ratio will be large and likely significant.
• Null Hypothesis (H0) : This is the hypothesis that there is no difference between the group means.
• Alternative Hypothesis (H1) : This is the hypothesis that there is a difference between at least two of the group means.
• p-value : This is the probability of obtaining a test statistic as extreme as the one that was actually observed, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected in favor of the alternative hypothesis.
• Post-hoc tests : These are follow-up tests conducted after an ANOVA when the null hypothesis is rejected, to determine which specific groups’ means (levels) are different from each other. Examples include Tukey’s HSD, Scheffe, Bonferroni, among others.

Types of ANOVA

Types of ANOVA are as follows:

One-way (or one-factor) ANOVA

This is the simplest type of ANOVA, which involves one independent variable . For example, comparing the effect of different types of diet (vegetarian, pescatarian, omnivore) on cholesterol level.

Two-way (or two-factor) ANOVA

This involves two independent variables. This allows for testing the effect of each independent variable on the dependent variable , as well as testing if there’s an interaction effect between the independent variables on the dependent variable.

Repeated Measures ANOVA

This is used when the same subjects are measured multiple times under different conditions, or at different points in time. This type of ANOVA is often used in longitudinal studies.

Mixed Design ANOVA

This combines features of both between-subjects (independent groups) and within-subjects (repeated measures) designs. In this model, one factor is a between-subjects variable and the other is a within-subjects variable.

Multivariate Analysis of Variance (MANOVA)

This is used when there are two or more dependent variables. It tests whether changes in the independent variable(s) correspond to changes in the dependent variables.

Analysis of Covariance (ANCOVA)

This combines ANOVA and regression. ANCOVA tests whether certain factors have an effect on the outcome variable after removing the variance for which quantitative covariates (interval variables) account. This allows the comparison of one variable outcome between groups, while statistically controlling for the effect of other continuous variables that are not of primary interest.

Nested ANOVA

This model is used when the groups can be clustered into categories. For example, if you were comparing students’ performance from different classrooms and different schools, “classroom” could be nested within “school.”

ANOVA Formulas

ANOVA Formulas are as follows:

Sum of Squares Total (SST)

This represents the total variability in the data. It is the sum of the squared differences between each observation and the overall mean.

• yi represents each individual data point
• y_mean represents the grand mean (mean of all observations)

Sum of Squares Within (SSW)

This represents the variability within each group or factor level. It is the sum of the squared differences between each observation and its group mean.

• yij represents each individual data point within a group
• y_meani represents the mean of the ith group

Sum of Squares Between (SSB)

This represents the variability between the groups. It is the sum of the squared differences between the group means and the grand mean, multiplied by the number of observations in each group.

• ni represents the number of observations in each group
• y_mean represents the grand mean

Degrees of Freedom

The degrees of freedom are the number of values that have the freedom to vary when calculating a statistic.

For within groups (dfW):

For between groups (dfB):

For total (dfT):

• N represents the total number of observations
• k represents the number of groups

Mean Squares

Mean squares are the sum of squares divided by the respective degrees of freedom.

Mean Squares Between (MSB):

Mean Squares Within (MSW):

F-Statistic

The F-statistic is used to test whether the variability between the groups is significantly greater than the variability within the groups.

If the F-statistic is significantly higher than what would be expected by chance, we reject the null hypothesis that all group means are equal.

Examples of ANOVA

Examples 1:

Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be measured using a stress rating scale.

Here are hypothetical stress ratings for a group of participants after they followed each of the exercise regimes for a period:

• Yoga: [3, 2, 2, 1, 2, 2, 3, 2, 1, 2]
• Aerobic Exercise: [2, 3, 3, 2, 3, 2, 3, 3, 2, 2]
• Weight Training: [4, 4, 5, 5, 4, 5, 4, 5, 4, 5]

The psychologist wants to determine if there is a statistically significant difference in stress levels between these different types of exercise.

To conduct the ANOVA:

1. State the hypotheses:

• Null Hypothesis (H0): There is no difference in mean stress levels between the three types of exercise.
• Alternative Hypothesis (H1): There is a difference in mean stress levels between at least two of the types of exercise.

2. Calculate the ANOVA statistics:

• Compute the Sum of Squares Between (SSB), Sum of Squares Within (SSW), and Sum of Squares Total (SST).
• Calculate the Degrees of Freedom (dfB, dfW, dfT).
• Calculate the Mean Squares Between (MSB) and Mean Squares Within (MSW).
• Compute the F-statistic (F = MSB / MSW).

3. Check the p-value associated with the calculated F-statistic.

• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This suggests there is a statistically significant difference in mean stress levels between the three exercise types.

4. Post-hoc tests

• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (exercise types) are different from each other.

Examples 2:

Suppose an agricultural scientist wants to compare the yield of three varieties of wheat. The scientist randomly selects four fields for each variety and plants them. After harvest, the yield from each field is measured in bushels. Here are the hypothetical yields:

The scientist wants to know if the differences in yields are due to the different varieties or just random variation.

Here’s how to apply the one-way ANOVA to this situation:

• Null Hypothesis (H0): The means of the three populations are equal.
• Alternative Hypothesis (H1): At least one population mean is different.
• Calculate the Degrees of Freedom (dfB for between groups, dfW for within groups, dfT for total).
• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This would suggest there is a statistically significant difference in mean yields among the three varieties.
• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (wheat varieties) are different from each other.

How to Conduct ANOVA

Conducting an Analysis of Variance (ANOVA) involves several steps. Here’s a general guideline on how to perform it:

• Null Hypothesis (H0): The means of all groups are equal.
• Alternative Hypothesis (H1): At least one group mean is different from the others.
• The significance level (often denoted as α) is usually set at 0.05. This implies that you are willing to accept a 5% chance that you are wrong in rejecting the null hypothesis.
• Data should be collected for each group under study. Make sure that the data meet the assumptions of an ANOVA: normality, independence, and homogeneity of variances.
• Calculate the Degrees of Freedom (df) for each sum of squares (dfB, dfW, dfT).
• Compute the Mean Squares Between (MSB) and Mean Squares Within (MSW) by dividing the sum of squares by the corresponding degrees of freedom.
• Compute the F-statistic as the ratio of MSB to MSW.
• Determine the critical F-value from the F-distribution table using dfB and dfW.
• If the calculated F-statistic is greater than the critical F-value, reject the null hypothesis.
• If the p-value associated with the calculated F-statistic is smaller than the significance level (0.05 typically), you reject the null hypothesis.
• If you rejected the null hypothesis, you can conduct post-hoc tests (like Tukey’s HSD) to determine which specific groups’ means (if you have more than two groups) are different from each other.
• Regardless of the result, report your findings in a clear, understandable manner. This typically includes reporting the test statistic, p-value, and whether the null hypothesis was rejected.

When to use ANOVA

ANOVA (Analysis of Variance) is used when you have three or more groups and you want to compare their means to see if they are significantly different from each other. It is a statistical method that is used in a variety of research scenarios. Here are some examples of when you might use ANOVA:

• Comparing Groups : If you want to compare the performance of more than two groups, for example, testing the effectiveness of different teaching methods on student performance.
• Evaluating Interactions : In a two-way or factorial ANOVA, you can test for an interaction effect. This means you are not only interested in the effect of each individual factor, but also whether the effect of one factor depends on the level of another factor.
• Repeated Measures : If you have measured the same subjects under different conditions or at different time points, you can use repeated measures ANOVA to compare the means of these repeated measures while accounting for the correlation between measures from the same subject.
• Experimental Designs : ANOVA is often used in experimental research designs when subjects are randomly assigned to different conditions and the goal is to compare the means of the conditions.

Here are the assumptions that must be met to use ANOVA:

• Normality : The data should be approximately normally distributed.
• Homogeneity of Variances : The variances of the groups you are comparing should be roughly equal. This assumption can be tested using Levene’s test or Bartlett’s test.
• Independence : The observations should be independent of each other. This assumption is met if the data is collected appropriately with no related groups (e.g., twins, matched pairs, repeated measures).

Applications of ANOVA

The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications:

Agriculture

ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods. For example, an agricultural researcher could use ANOVA to determine if there are significant differences in the yields of several varieties of wheat under the same conditions.

Manufacturing and Quality Control

ANOVA is used to determine if different manufacturing processes or machines produce different levels of product quality. For instance, an engineer might use it to test whether there are differences in the strength of a product based on the machine that produced it.

Marketing Research

Marketers often use ANOVA to test the effectiveness of different advertising strategies. For example, a marketer could use ANOVA to determine whether different marketing messages have a significant impact on consumer purchase intentions.

Healthcare and Medicine

In medical research, ANOVA can be used to compare the effectiveness of different treatments or drugs. For example, a medical researcher could use ANOVA to test whether there are significant differences in recovery times for patients who receive different types of therapy.

ANOVA is used in educational research to compare the effectiveness of different teaching methods or educational interventions. For example, an educator could use it to test whether students perform significantly differently when taught with different teaching methods.

Psychology and Social Sciences

Psychologists and social scientists use ANOVA to compare group means on various psychological and social variables. For example, a psychologist could use it to determine if there are significant differences in stress levels among individuals in different occupations.

Biology and Environmental Sciences

Biologists and environmental scientists use ANOVA to compare different biological and environmental conditions. For example, an environmental scientist could use it to determine if there are significant differences in the levels of a pollutant in different bodies of water.

Advantages of ANOVA

Here are some advantages of using ANOVA:

Comparing Multiple Groups: One of the key advantages of ANOVA is the ability to compare the means of three or more groups. This makes it more powerful and flexible than the t-test, which is limited to comparing only two groups.

Control of Type I Error: When comparing multiple groups, the chances of making a Type I error (false positive) increases. One of the strengths of ANOVA is that it controls the Type I error rate across all comparisons. This is in contrast to performing multiple pairwise t-tests which can inflate the Type I error rate.

Testing Interactions: In factorial ANOVA, you can test not only the main effect of each factor, but also the interaction effect between factors. This can provide valuable insights into how different factors or variables interact with each other.

Handling Continuous and Categorical Variables: ANOVA can handle both continuous and categorical variables . The dependent variable is continuous and the independent variables are categorical.

Robustness: ANOVA is considered robust to violations of normality assumption when group sizes are equal. This means that even if your data do not perfectly meet the normality assumption, you might still get valid results.

Provides Detailed Analysis: ANOVA provides a detailed breakdown of variances and interactions between variables which can be useful in understanding the underlying factors affecting the outcome.

Capability to Handle Complex Experimental Designs: Advanced types of ANOVA (like repeated measures ANOVA, MANOVA, etc.) can handle more complex experimental designs, including those where measurements are taken on the same subjects over time, or when you want to analyze multiple dependent variables at once.

Disadvantages of ANOVA

Some limitations or disadvantages that are important to consider:

Assumptions: ANOVA relies on several assumptions including normality (the data follows a normal distribution), independence (the observations are independent of each other), and homogeneity of variances (the variances of the groups are roughly equal). If these assumptions are violated, the results of the ANOVA may not be valid.

Sensitivity to Outliers: ANOVA can be sensitive to outliers. A single extreme value in one group can affect the sum of squares and consequently influence the F-statistic and the overall result of the test.

Dichotomous Variables: ANOVA is not suitable for dichotomous variables (variables that can take only two values, like yes/no or male/female). It is used to compare the means of groups for a continuous dependent variable.

Lack of Specificity: Although ANOVA can tell you that there is a significant difference between groups, it doesn’t tell you which specific groups are significantly different from each other. You need to carry out further post-hoc tests (like Tukey’s HSD or Bonferroni) for these pairwise comparisons.

Complexity with Multiple Factors: When dealing with multiple factors and interactions in factorial ANOVA, interpretation can become complex. The presence of interaction effects can make main effects difficult to interpret.

Requires Larger Sample Sizes: To detect an effect of a certain size, ANOVA generally requires larger sample sizes than a t-test.

Equal Group Sizes: While not always a strict requirement, ANOVA is most powerful and its assumptions are most likely to be met when groups are of equal or similar sizes.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

Graphical Methods – Types, Examples and Guide

Substantive Framework – Types, Methods and...

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 16.

• ANOVA 1: Calculating SST (total sum of squares)
• ANOVA 2: Calculating SSW and SSB (total sum of squares within and between)

ANOVA 3: Hypothesis test with F-statistic

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Lesson 10: introduction to anova, overview section  .

In the previous lessons, we learned how to perform inference for a population mean from one sample and also how to compare population means from two samples (independent and paired). In this Lesson, we introduce Analysis of Variance or ANOVA. ANOVA is a statistical method that analyzes variances to determine if the means from more than two populations are the same. In other words, we have a quantitative response variable and a categorical explanatory variable with more than two levels. In ANOVA, the categorical explanatory is typically referred to as the factor.

• Describe the logic behind analysis of variance.
• Set up and perform one-way ANOVA.
• Identify the information in the ANOVA table.
• Interpret the results from ANOVA output.
• Perform multiple comparisons and interpret the results, when appropriate.

13.1 One-Way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups

H 0 : μ 1 = μ 2 = μ 3 = ... = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , ..., μ k are not equal. That is, μ i ≠ μ j for some i ≠ j .

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger, which is caused by the different means as shown in the second graph (green box plots).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/13-1-one-way-anova

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Statistics Made Easy

4 Examples of Using ANOVA in Real Life

Often when students learn about a certain topic in school, they’re inclined to ask:

“When is this ever used in real life?”

This is often the case in statistics, when certain techniques and methods seem so obscure that it’s hard to imagine them actually being applied in real-life situations.

However, the ANOVA (short for “analysis of variance”) is a technique that is actually used all the time in a variety of fields in real life.

In this post, we’ll share a quick refresher on what an ANOVA is along with four examples of how it is used in real life situations.

What is an ANOVA?

An  ANOVA  (“Analysis of Variance”) is a statistical technique that is used to determine whether or not there is a significant difference between the means of three or more independent groups. The two most common types of ANOVAs are the one-way ANOVA and two-way ANOVA.

A One-Way ANOVA  is used to determine how one factor impacts a response variable. For example, we might want to know if three different studying techniques lead to different mean exam scores. To see if there is a statistically significant difference in mean exam scores, we can conduct a one-way ANOVA.

A Two-Way ANOVA  is used to determine how two factors impact a response variable, and to determine whether or not there is an interaction between the two factors on the response variable. For example, we might want to know how gender and how different levels of exercise impact average weight loss. We would conduct a two-way ANOVA to find out.

It’s also possible to conduct a three-way ANOVA, four-way ANOVA, etc. but these are much more uncommon and it can be difficult to interpret ANOVA results if too many factors are used.

Now we will share four different examples of when ANOVA’s are actually used in real life.

ANOVA Real Life Example #1

A large scale farm is interested in understanding which of three different fertilizers leads to the highest crop yield. They sprinkle each fertilizer on ten different fields and measure the total yield at the end of the growing season.

To understand whether there is a statistically significant difference in the mean yield that results from these three fertilizers, researchers can conduct a one-way ANOVA, using “type of fertilizer” as the factor and “crop yield” as the response.

If the overall p-value of the ANOVA is lower than our significance level (typically chosen to be 0.10, 0.05, 0.01) then we can conclude that there is a statistically significant difference in mean crop yield between the three fertilizers. We can then conduct post hoc tests to determine exactly which fertilizer lead to the highest mean yield.

ANOVA Real Life Example #2

Medical researchers want to know if four different medications lead to different mean blood pressure reductions in patients. They randomly assign 20 patients to use each medication for one month, then measure the blood pressure both before and after the patient started using the medication to find the mean blood pressure reduction for each medication.

To understand whether there is a statistically significant difference in the mean blood pressure reduction that results from these medications, researchers can conduct a one-way ANOVA, using “type of medication” as the factor and “blood pressure reduction” as the response.

If the overall p-value of the ANOVA is lower than our significance level, then we can conclude that there is a statistically significant difference in mean blood pressure reduction between the four medications. We can then conduct post hoc tests to determine exactly which medications lead to significantly different results.

ANOVA Real Life Example #3

A grocery chain wants to know if three different types of advertisements affect mean sales differently. They use each type of advertisement at 10 different stores for one month and measure total sales for each store at the end of the month.

To see if there is a statistically significant difference in mean sales between these three types of advertisements, researchers can conduct a one-way ANOVA, using “type of advertisement” as the factor and “sales” as the response variable.

If the overall p-value of the ANOVA is lower than our significance level, then we can conclude that there is a statistically significant difference in mean sales between the three types of advertisements. We can then conduct post hoc tests to determine exactly which types of advertisements lead to significantly different results.

ANOVA Real Life Example #4

Biologists want to know how different levels of sunlight exposure (no sunlight, low sunlight, medium sunlight, high sunlight) and watering frequency (daily, weekly) impact the growth of a certain plant. In this case, two factors are involved (level of sunlight exposure and water frequency), so they will conduct a two-way ANOVA to see if either factor significantly impacts plant growth and whether or not the two factors are related to each other.

The results of the ANOVA will tell us whether each individual factor has a significant effect on plant growth. Using this information, the biologists can better understand which level of sunlight exposure and/or watering frequency leads to optimal growth.

ANOVA is used in a wide variety of real-life situations, but the most common include:

• Retail:  Store are often interested in understanding whether different types of promotions, store layouts, advertisement tactics, etc. lead to different sales. This is the exact type of analysis that ANOVA is built for.
• Medical:  Researchers are often interested in whether or not different medications affect patients differently, which is why they often use one-way or two-way ANOVA’s in these situations.
• Environmental Sciences:  Researchers are often interested in understanding how different levels of factors affect plants and wildlife. Because of the nature of these types of analyses, ANOVA’s are often used.

So, next time someone asks you when an ANOVA is actually used in real life, feel free to reference these examples!

Additional Resources

An Introduction to the One-Way ANOVA An Introduction to the Two-Way ANOVA The Differences Between ANOVA, ANCOVA, MANOVA, and MANCOVA

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “4 Examples of Using ANOVA in Real Life”

Those examples are the real labs exercises required for those topics, with them, I had no need for further explanation before I got good understanding of them. Well done!

Hello Zach, I hope I get a reply to this. I am a first year doctoral student who has had a rocky foundation with statistics. I am taking statistics course again years after my masters and I come to this website to read your write ups which make me understand my class materials better. I quote you in my assignments all the time but I think you deserve to know that I had an A. I would love to keep in touch but if I can’t, that is okay. I look forward to reading from you as I would be taking another stats course next semester. Enjoy your day. Thank you.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

ANOVA Test is used to analyze the differences among the means of various groups using certain estimation procedures. ANOVA means analysis of variance. ANOVA test is a statistical significance test that is used to check whether the null hypothesis can be rejected or not during hypothesis testing.

An ANOVA test can be either one-way or two-way depending upon the number of independent variables. In this article, we will learn more about an ANOVA test, the one-way ANOVA and two-way ANOVA, its formulas and see certain associated examples.

What is ANOVA Test?

ANOVA test, in its simplest form, is used to check whether the means of three or more populations are equal or not. The ANOVA test applies when there are more than two independent groups. The goal of the ANOVA test is to check for variability within the groups as well as the variability among the groups. The ANOVA test statistic is given by the f test .

ANOVA Test Definition

ANOVA test can be defined as a type of test used in hypothesis testing to compare whether the means of two or more groups are equal or not. This test is used to check if the null hypothesis can be rejected or not depending upon the statistical significance exhibited by the parameters. The decision is made by comparing the ANOVA test statistic with the critical value.

ANOVA Test Example

Suppose it needs to be determined if consumption of a certain type of tea will result in a mean weight loss. Let there be three groups using three types of tea - green tea, earl grey tea, and jasmine tea. Thus, to compare if there was any mean weight loss exhibited by a certain group, the ANOVA test (one way) will be used.

Suppose a survey was conducted to check if there is an interaction between income and gender with anxiety level at job interviews. To conduct such a test a two-way ANOVA will be used.

ANOVA Formula

There are several components to the ANOVA formula. The best way to solve a problem on an ANOVA test is by organizing the formulas into an ANOVA table. The ANOVA formulas are given below.

Sum of squares between groups, SSB = \(\sum n_{j}(\overline{X}_{j}-\overline{X})^{2}\). Here, \(\overline{X}_{j}\) is the mean of the j th group, \(\overline{X}\) is the overall mean and \(n_{j}\) is the sample size of the j th group.

\(\overline{X}\) = \(\frac{\overline{X}_{1} + \overline{X}_{2} + \overline{X}_{3} + ... + \overline{X}_{j}}{j}\)

Sum of squares of errors, SSE = \(\sum\sum(X-\overline{X}_{j})^{2}\). Here, X refers to each data point in the j th group.

Total sum of squares, SST = SSB + SSE

Degrees of freedom between groups, df 1 = k - 1. Here, k denotes the number of groups.

Degrees of freedom of errors, df 2 = N - k, where N denotes the total number of observations across k groups.

Total degrees of freedom, df 3 = N - 1.

Mean squares between groups, MSB = SSB / (k - 1)

Mean squares of errors, MSE = SSE / (N - k)

ANOVA test statistic, f = MSB / MSE

Critical Value at \(\alpha\) = F(\(\alpha\), k - 1, N - k)

ANOVA Table

The ANOVA formulas can be arranged systematically in the form of a table. This ANOVA table can be summarized as follows:

One Way ANOVA

The one way ANOVA test is used to determine whether there is any difference between the means of three or more groups. A one way ANOVA will have only one independent variable. The hypothesis for a one way ANOVA test can be set up as follows:

Null Hypothesis, \(H_{0}\): \(\mu_{1}\) = \(\mu_{2}\) = \(\mu_{3}\) = ... = \(\mu_{k}\)

Alternative Hypothesis, \(H_{1}\): The means are not equal

Decision Rule: If test statistic > critical value then reject the null hypothesis and conclude that the means of at least two groups are statistically significant.

The steps to perform the one way ANOVA test are given below:

• Step 1: Calculate the mean for each group.
• Step 2: Calculate the total mean. This is done by adding all the means and dividing it by the total number of means.
• Step 3: Calculate the SSB.
• Step 4: Calculate the between groups degrees of freedom.
• Step 5: Calculate the SSE.
• Step 6: Calculate the degrees of freedom of errors.
• Step 7: Determine the MSB and the MSE.
• Step 8: Find the f test statistic.
• Step 9: Using the f table for the specified level of significance, \(\alpha\), find the critical value. This is given by F(\(\alpha\), df 1 . df 2 ).
• Step 10: If f > F then reject the null hypothesis.

Limitations of One Way ANOVA Test

The one way ANOVA is an omnibus test statistic. This implies that the test will determine whether the means of the various groups are statistically significant or not. However, it cannot distinguish the specific groups that have a statistically significant mean. Thus, to find the specific group with a different mean, a post hoc test needs to be conducted.

Two Way ANOVA

The two way ANOVA has two independent variables. Thus, it can be thought of as an extension of a one way ANOVA where only one variable affects the dependent variable. A two way ANOVA test is used to check the main effect of each independent variable and to see if there is an interaction effect between them. To examine the main effect, each factor is considered separately as done in a one way ANOVA. Furthermore, to check the interaction effect, all factors are considered at the same time. There are certain assumptions made for a two way ANOVA test. These are given as follows:

• The samples drawn from the population must be independent.
• The population should be approximately normally distributed.
• The groups should have the same sample size.
• The population variances are equal

Suppose in the two way ANOVA example, as mentioned above, the income groups are low, middle, high. The gender groups are female, male, and transgender. Then there will be 9 treatment groups and the three hypotheses can be set up as follows:

\(H_{01}\): All income groups have equal mean anxiety.

\(H_{11}\): All income groups do not have equal mean anxiety.

\(H_{02}\): All gender groups have equal mean anxiety.

\(H_{12}\): All gender groups do not have equal mean anxiety.

\(H_{03}\): Interaction effect does not exist

\(H_{13}\): Interaction effect exists.

Related Articles:

• Probability and Statistics
• Data Handling
• Z Score Formula

Important Notes on ANOVA Test

• ANOVA test is used to check whether the means of three or more groups are different or not by using estimation parameters such as the variance.
• An ANOVA table is used to summarize the results of an ANOVA test.
• There are two types of ANOVA tests - one way ANOVA and two way ANOVA
• One way ANOVA has only one independent variable while a two way ANOVA has two independent variables.

Examples on ANOVA Test

Example 1: Three types of fertilizers are used on three groups of plants for 5 weeks. We want to check if there is a difference in the mean growth of each group. Using the data given below apply a one way ANOVA test at 0.05 significant level.

\(H_{0}\): \(\mu_{1}\) = \(\mu_{2}\) = \(\mu_{3}\)

\(H_{1}\): The means are not equal

Total mean, \(\overline{X}\) = 8

\(n_{1}\) = \(n_{2}\) = \(n_{3}\) = 6, k = 3

SSB = 6(5 - 8) 2 + 6(9 - 8) 2 + 6(10 - 8) 2

df 1 = k - 1 = 2

SSE = 16 + 24 + 28 = 68

df 2 = N - k = 18 - 3 = 15

MSB = SSB / df 1 = 84 / 2 = 42

MSE = SSE / df 2 = 68 / 15 = 4.53

ANOVA test statistic, f = MSB / MSE = 42 / 4.53 = 9.33

Using the f table at \(\alpha\) = 0.05 the critical value is given as F(0.05, 2, 15) = 3.68

As f > F, thus, the null hypothesis is rejected and it can be concluded that there is a difference in the mean growth of the plants.

Answer: Reject the null hypothesis

Example 2: A trial was run to check the effects of different diets. Positive numbers indicate weight loss and negative numbers indicate weight gain. Check if there is an average difference in the weight of people following different diets using an ANOVA Table.

\(H_{0}\): \(\mu_{1}\) = \(\mu_{2}\) = \(\mu_{3}\) = \(\mu_{4}\)

Total mean, \(\overline{X}\) = 3.6

\(n_{1}\) = \(n_{2}\) = \(n_{3}\) = \(n_{4}\) = 5, k = 4

SSB = \(n_{1}(\overline{X}_{1}-\overline{X})^{2}\) + \(n_{2}(\overline{X}_{2}-\overline{X})^{2}\) +& \(n_{3}(\overline{X}_{3}-\overline{X})^{2}\) +\(n_{4}(\overline{X}_{4}-\overline{X})^{2}\)

SSE = 21.4 + 10 + 5.4 + 10.6 = 47.4

The ANOVA Table can be constructed as follows:

As no significance level is specified, \(\alpha\) = 0.05 is chosen.

F(0.05, 3, 16) = 3.24

As 8.43 > 3.24, thus, the null hypothesis is rejected and it can be concluded that there is a mean weight loss in the diets.

Example 3: Determine if there is a difference in the mean daily calcium intake for people with normal bone density, osteopenia, and osteoporosis at a 0.05 alpha level. The data was recorded as follows:

Using the ANOVA test the hypothesis is set up as follows:

Total mean, \(\overline{X}\) = 817.8

SSB = \(n_{1}(\overline{X}_{1}-\overline{X})^{2}\) + \(n_{2}(\overline{X}_{2}-\overline{X})^{2}\) + \(n_{3}(\overline{X}_{3}-\overline{X})^{2}\)

= 152,477.7

SSE = 130,083.3 + 240,000 + 449,750 = 819,833.3

Using the F table the critical value is F(0.05, 2, 15) = 3.68

As 1.395 < 3.68, the null hypothesis cannot be rejected and it is concluded that there is not enough evidence to prove that the mean daily calcium intake of the three groups is different.

Answer: Do not reject the null hypothesis

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on ANOVA Test

What is an anova test in statistics.

ANOVA test in statistics refers to a hypothesis test that analyzes the variances of three or more populations to determine if the means are different or not.

How to Set Up the Hypothesis for an ANOVA Test?

In an ANOVA test the equality of the means of different groups has to be examined. Thus, the hypothesis is set up as follows:

What is the Formula for the ANOVA Test Statistic?

The ANOVA test uses the F statistic. The formula for the test statistic is given as F = mean squares between groups (MSB) / mean square between errors (MSE)

What is an ANOVA Table?

An ANOVA table is a table that is used to summarize the findings of an ANOVA test. There are 5 columns that consist of the source of variation, the sum of squares, degrees of freedom, mean squares, and the f statistic respectively.

How to Perform an ANOVA Test?

The steps to perform an ANOVA test are as follows:

• Set up the hypothesis.
• Find the means of each group and then determine the overall mean.
• Find the SSB and the corresponding degrees of freedom.
• Determine the SSE and the degrees of freedom.
• Find the MSB and the MSE.
• Divide the MSB by the MSE to find the test statistic.
• Compare the test statistic with the critical value to determine statistical significance.

What is a One Way ANOVA?

One way ANOVA is a type of ANOVA test that is conducted when there is only one independent variable. It is used to compare the means of the various test groups. Such a test can only give information on the statistical significance of the means however, it cannot determine which groups have the differing means.

What is a Two Way ANOVA?

A two way ANOVA is an extension of a one way ANOVA and is conducted when there are two independent variables. It is used to find the main effect as well as the interaction effect of the different factors.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.2: One-Way ANOVA

• Last updated
• Save as PDF
• Page ID 807

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are several basic assumptions to be fulfilled:

Five basic assumptions of one-way ANOVA to be fulfilled

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are \(k\) groups:

• \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \dotsc = \mu_{k}\)
• \(H_{a}: \text{At least two of the group means} \mu_{2} = \mu_{3} = \dotsc = \mu_{k} \text{are not equal}\)

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3}\) and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

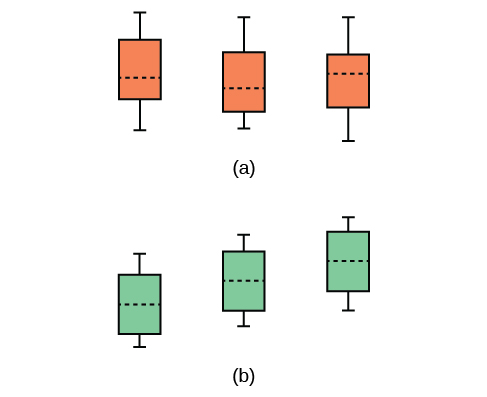
Analysis of variance extends the comparison of two groups to several, each a level of a categorical variable (factor). Samples from each group are independent, and must be randomly selected from normal populations with equal variances. We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the \(F\) distribution with two different degrees of freedom.

Assumptions:

• all populations of interest are normally distributed.
• the populations have equal standard deviations.
• samples (not necessarily of the same size) are randomly and independently selected from each population.

The test statistic for analysis of variance is the \(F\)-ratio.

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Get science-backed answers as you write with Paperpal's Research feature

How to Write a Hypothesis? Types and Examples 

All research studies involve the use of the scientific method, which is a mathematical and experimental technique used to conduct experiments by developing and testing a hypothesis or a prediction about an outcome. Simply put, a hypothesis is a suggested solution to a problem. It includes elements that are expressed in terms of relationships with each other to explain a condition or an assumption that hasn’t been verified using facts. 1 The typical steps in a scientific method include developing such a hypothesis, testing it through various methods, and then modifying it based on the outcomes of the experiments.  

A research hypothesis can be defined as a specific, testable prediction about the anticipated results of a study. 2 Hypotheses help guide the research process and supplement the aim of the study. After several rounds of testing, hypotheses can help develop scientific theories. 3 Hypotheses are often written as if-then statements. 

Here are two hypothesis examples: 

Dandelions growing in nitrogen-rich soils for two weeks develop larger leaves than those in nitrogen-poor soils because nitrogen stimulates vegetative growth. 4  

If a company offers flexible work hours, then their employees will be happier at work. 5  

Table of Contents

• What is a hypothesis? 
• Types of hypotheses 
• Characteristics of a hypothesis 
• Functions of a hypothesis 
• How to write a hypothesis 
• Hypothesis examples 
• Frequently asked questions 

What is a hypothesis?

A hypothesis expresses an expected relationship between variables in a study and is developed before conducting any research. Hypotheses are not opinions but rather are expected relationships based on facts and observations. They help support scientific research and expand existing knowledge. An incorrectly formulated hypothesis can affect the entire experiment leading to errors in the results so it’s important to know how to formulate a hypothesis and develop it carefully.

A few sources of a hypothesis include observations from prior studies, current research and experiences, competitors, scientific theories, and general conditions that can influence people. Figure 1 depicts the different steps in a research design and shows where exactly in the process a hypothesis is developed. 4  

There are seven different types of hypotheses—simple, complex, directional, nondirectional, associative and causal, null, and alternative. 

Types of hypotheses

The seven types of hypotheses are listed below: 5 , 6,7  

• Simple : Predicts the relationship between a single dependent variable and a single independent variable. 

Example: Exercising in the morning every day will increase your productivity.  

• Complex : Predicts the relationship between two or more variables. 

Example: Spending three hours or more on social media daily will negatively affect children’s mental health and productivity, more than that of adults.  

• Directional : Specifies the expected direction to be followed and uses terms like increase, decrease, positive, negative, more, or less. 

Example: The inclusion of intervention X decreases infant mortality compared to the original treatment.  

• Non-directional : Does not predict the exact direction, nature, or magnitude of the relationship between two variables but rather states the existence of a relationship. This hypothesis may be used when there is no underlying theory or if findings contradict prior research. 

Example: Cats and dogs differ in the amount of affection they express.  

• Associative and causal : An associative hypothesis suggests an interdependency between variables, that is, how a change in one variable changes the other.  

Example: There is a positive association between physical activity levels and overall health.  

A causal hypothesis, on the other hand, expresses a cause-and-effect association between variables. 

Example: Long-term alcohol use causes liver damage.  

• Null : Claims that the original hypothesis is false by showing that there is no relationship between the variables. 

Example: Sleep duration does not have any effect on productivity.  

• Alternative : States the opposite of the null hypothesis, that is, a relationship exists between two variables. 

Example: Sleep duration affects productivity.  

Characteristics of a hypothesis

So, what makes a good hypothesis? Here are some important characteristics of a hypothesis. 8,9  

• Testable : You must be able to test the hypothesis using scientific methods to either accept or reject the prediction. 
• Falsifiable : It should be possible to collect data that reject rather than support the hypothesis. 
• Logical : Hypotheses shouldn’t be a random guess but rather should be based on previous theories, observations, prior research, and logical reasoning. 
• Positive : The hypothesis statement about the existence of an association should be positive, that is, it should not suggest that an association does not exist. Therefore, the language used and knowing how to phrase a hypothesis is very important. 
• Clear and accurate : The language used should be easily comprehensible and use correct terminology. 
• Relevant : The hypothesis should be relevant and specific to the research question. 
• Structure : Should include all the elements that make a good hypothesis: variables, relationship, and outcome. 

Functions of a hypothesis

The following list mentions some important functions of a hypothesis: 1  

• Maintains the direction and progress of the research. 
• Expresses the important assumptions underlying the proposition in a single statement. 
• Establishes a suitable context for researchers to begin their investigation and for readers who are referring to the final report. 
• Provides an explanation for the occurrence of a specific phenomenon. 
• Ensures selection of appropriate and accurate facts necessary and relevant to the research subject. 

To summarize, a hypothesis provides the conceptual elements that complete the known data, conceptual relationships that systematize unordered elements, and conceptual meanings and interpretations that explain the unknown phenomena. 1  

How to write a hypothesis

Listed below are the main steps explaining how to write a hypothesis. 2,4,5  

• Make an observation and identify variables : Observe the subject in question and try to recognize a pattern or a relationship between the variables involved. This step provides essential background information to begin your research.  

For example, if you notice that an office’s vending machine frequently runs out of a specific snack, you may predict that more people in the office choose that snack over another. 

• Identify the main research question : After identifying a subject and recognizing a pattern, the next step is to ask a question that your hypothesis will answer.  

For example, after observing employees’ break times at work, you could ask “why do more employees take breaks in the morning rather than in the afternoon?” 

• Conduct some preliminary research to ensure originality and novelty : Your initial answer, which is your hypothesis, to the question is based on some pre-existing information about the subject. However, to ensure that your hypothesis has not been asked before or that it has been asked but rejected by other researchers you would need to gather additional information.  

For example, based on your observations you might state a hypothesis that employees work more efficiently when the air conditioning in the office is set at a lower temperature. However, during your preliminary research you find that this hypothesis was proven incorrect by a prior study. 

• Develop a general statement : After your preliminary research has confirmed the originality of your proposed answer, draft a general statement that includes all variables, subjects, and predicted outcome. The statement could be if/then or declarative.  
• Finalize the hypothesis statement : Use the PICOT model, which clarifies how to word a hypothesis effectively, when finalizing the statement. This model lists the important components required to write a hypothesis. 

P opulation: The specific group or individual who is the main subject of the research 

I nterest: The main concern of the study/research question 

C omparison: The main alternative group 

O utcome: The expected results  

T ime: Duration of the experiment 

Once you’ve finalized your hypothesis statement you would need to conduct experiments to test whether the hypothesis is true or false. 

Hypothesis examples

The following table provides examples of different types of hypotheses. 10 ,11  

Key takeaways  

Here’s a summary of all the key points discussed in this article about how to write a hypothesis. 

• A hypothesis is an assumption about an association between variables made based on limited evidence, which should be tested. 
• A hypothesis has four parts—the research question, independent variable, dependent variable, and the proposed relationship between the variables.   
• The statement should be clear, concise, testable, logical, and falsifiable. 
• There are seven types of hypotheses—simple, complex, directional, non-directional, associative and causal, null, and alternative. 
• A hypothesis provides a focus and direction for the research to progress. 
• A hypothesis plays an important role in the scientific method by helping to create an appropriate experimental design. 

Frequently asked questions

Hypotheses and research questions have different objectives and structure. The following table lists some major differences between the two. 9  

Here are a few examples to differentiate between a research question and hypothesis. 

Yes, here’s a simple checklist to help you gauge the effectiveness of your hypothesis. 9   1. When writing a hypothesis statement, check if it:  2. Predicts the relationship between the stated variables and the expected outcome.  3. Uses simple and concise language and is not wordy.  4. Does not assume readers’ knowledge about the subject.  5. Has observable, falsifiable, and testable results. 

As mentioned earlier in this article, a hypothesis is an assumption or prediction about an association between variables based on observations and simple evidence. These statements are usually generic. Research objectives, on the other hand, are more specific and dictated by hypotheses. The same hypothesis can be tested using different methods and the research objectives could be different in each case.     For example, Louis Pasteur observed that food lasts longer at higher altitudes, reasoned that it could be because the air at higher altitudes is cleaner (with fewer or no germs), and tested the hypothesis by exposing food to air cleaned in the laboratory. 12 Thus, a hypothesis is predictive—if the reasoning is correct, X will lead to Y—and research objectives are developed to test these predictions. 

Null hypothesis testing is a method to decide between two assumptions or predictions between variables (null and alternative hypotheses) in a statistical relationship in a sample. The null hypothesis, denoted as H 0 , claims that no relationship exists between variables in a population and any relationship in the sample reflects a sampling error or occurrence by chance. The alternative hypothesis, denoted as H 1 , claims that there is a relationship in the population. In every study, researchers need to decide whether the relationship in a sample occurred by chance or reflects a relationship in the population. This is done by hypothesis testing using the following steps: 13   1. Assume that the null hypothesis is true.  2. Determine how likely the sample relationship would be if the null hypothesis were true. This probability is called the p value.  3. If the sample relationship would be extremely unlikely, reject the null hypothesis and accept the alternative hypothesis. If the relationship would not be unlikely, accept the null hypothesis. 

To summarize, researchers should know how to write a good hypothesis to ensure that their research progresses in the required direction. A hypothesis is a testable prediction about any behavior or relationship between variables, usually based on facts and observation, and states an expected outcome.  

We hope this article has provided you with essential insight into the different types of hypotheses and their functions so that you can use them appropriately in your next research project. 

References  

• Dalen, DVV. The function of hypotheses in research. Proquest website. Accessed April 8, 2024. https://www.proquest.com/docview/1437933010?pq-origsite=gscholar&fromopenview=true&sourcetype=Scholarly%20Journals&imgSeq=1  
• McLeod S. Research hypothesis in psychology: Types & examples. SimplyPsychology website. Updated December 13, 2023. Accessed April 9, 2024. https://www.simplypsychology.org/what-is-a-hypotheses.html  
• Scientific method. Britannica website. Updated March 14, 2024. Accessed April 9, 2024. https://www.britannica.com/science/scientific-method  
• The hypothesis in science writing. Accessed April 10, 2024. https://berks.psu.edu/sites/berks/files/campus/HypothesisHandout_Final.pdf  
• How to develop a hypothesis (with elements, types, and examples). Indeed.com website. Updated February 3, 2023. Accessed April 10, 2024. https://www.indeed.com/career-advice/career-development/how-to-write-a-hypothesis  
• Types of research hypotheses. Excelsior online writing lab. Accessed April 11, 2024. https://owl.excelsior.edu/research/research-hypotheses/types-of-research-hypotheses/  
• What is a research hypothesis: how to write it, types, and examples. Researcher.life website. Published February 8, 2023. Accessed April 11, 2024. https://researcher.life/blog/article/how-to-write-a-research-hypothesis-definition-types-examples/  
• Developing a hypothesis. Pressbooks website. Accessed April 12, 2024. https://opentext.wsu.edu/carriecuttler/chapter/developing-a-hypothesis/  
• What is and how to write a good hypothesis in research. Elsevier author services website. Accessed April 12, 2024. https://scientific-publishing.webshop.elsevier.com/manuscript-preparation/what-how-write-good-hypothesis-research/  
• How to write a great hypothesis. Verywellmind website. Updated March 12, 2023. Accessed April 13, 2024. https://www.verywellmind.com/what-is-a-hypothesis-2795239  
• 15 Hypothesis examples. Helpfulprofessor.com Published September 8, 2023. Accessed March 14, 2024. https://helpfulprofessor.com/hypothesis-examples/ 
• Editage insights. What is the interconnectivity between research objectives and hypothesis? Published February 24, 2021. Accessed April 13, 2024. https://www.editage.com/insights/what-is-the-interconnectivity-between-research-objectives-and-hypothesis  
• Understanding null hypothesis testing. BCCampus open publishing. Accessed April 16, 2024. https://opentextbc.ca/researchmethods/chapter/understanding-null-hypothesis-testing/#:~:text=In%20null%20hypothesis%20testing%2C%20this,said%20to%20be%20statistically%20significant  

Paperpal is a comprehensive AI writing toolkit that helps students and researchers achieve 2x the writing in half the time. It leverages 21+ years of STM experience and insights from millions of research articles to provide in-depth academic writing, language editing, and submission readiness support to help you write better, faster.  

Get accurate academic translations, rewriting support, grammar checks, vocabulary suggestions, and generative AI assistance that delivers human precision at machine speed. Try for free or upgrade to Paperpal Prime starting at US$19 a month to access premium features, including consistency, plagiarism, and 30+ submission readiness checks to help you succeed.  

Experience the future of academic writing – Sign up to Paperpal and start writing for free!  

Related Reads:

• Empirical Research: A Comprehensive Guide for Academics 
• How to Write a Scientific Paper in 10 Steps 
• What is a Literature Review? How to Write It (with Examples)
• What are Journal Guidelines on Using Generative AI Tools

Measuring Academic Success: Definition & Strategies for Excellence

What are scholarly sources and where can you find them , you may also like, 4 ways paperpal encourages responsible writing with ai, what are scholarly sources and where can you..., what is academic writing: tips for students, why traditional editorial process needs an upgrade, paperpal’s new ai research finder empowers authors to..., what is hedging in academic writing  , how to use ai to enhance your college..., ai + human expertise – a paradigm shift..., how to use paperpal to generate emails &....