problem solving strategies in mathematics in modern world

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 9823

• Michelle Manes
• University of Hawaii

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

Problem Solving Strategy 2 (Try Something!).

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

Problem Solving Strategy 3 (Draw a Picture).

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

Problem Solving Strategy 4 (Make Up Numbers).

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”

Problem Solving Strategy 5 (Try a Simpler Problem).

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

Problem Solving Strategy 6 (Work Systematically).

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate).

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

Problem Solving Strategy 8 (Look for and Explain Patterns).

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table.
• Can you explain and justify any of the patterns you see? How can you be sure they will continue?
• What calculation would you do to find the total number of squares on a 100 × 100 chess board?

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

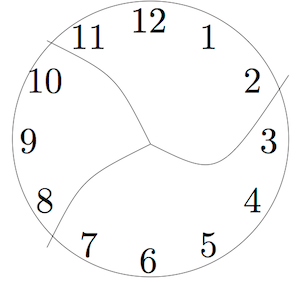
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?

Problem Solving Strategy 9 (Find the Math, Remove the Context).

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

Problem Solving Strategy 10 (Check Your Assumptions).

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

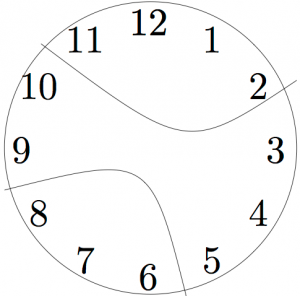
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

Problem-Solving in Mathematics Education

• Reference work entry
• First Online: 01 January 2020
• Cite this reference work entry

• Manuel Santos-Trigo 2  

1258 Accesses

8 Citations

Introduction

Problem-solving approaches appear in all human endeavors. In mathematics, activities such as posing or defining problems and looking for different ways to solve them are central to the development of the discipline. In mathematics education, the systematic study of what the process of formulating and solving problems entails and the ways to structure problem-solving approaches to learn mathematics has been part of the research agenda in mathematics education. How have research and practicing problem-solving approaches changed and evolved in mathematics education, and what themes are currently investigated? Two communities have significantly contributed to the characterization and development of the research and practicing agenda in mathematical problem-solving: mathematicians who recognize that the process of formulating, representing, and solving problems is essential in the development of mathematical knowledge (Polya 1945 ; Hadamard 1945 ; Halmos 1980 ) and mathematics...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Artigue M, Houdement C (2007) Problem solving in France: didactic and curricular perspectives. ZDM Int J Math Educ 39(5–6):365–382

Article   Google Scholar  

Cai J, Nie B (2007) Problem solving in Chinese mathematics education: research and practice. ZDM Int J Math Educ 39(5–6):459–473

Common Core State Standards for Mathematics (CCSS) (2010) Common Core State Standards initiative. http://www.corestandards.org/

Devlin K (2002) The millennium problems. The seven greatest unsolved mathematical puzzles of our time. Granta Publications, London

Google Scholar  

Dick TP, Hollebrands K (2011) Focus in high school mathematics: technology to support reasoning and sense making. The National Council of Teachers of Mathematics, Reston

Doorman M, Drijvers P, Dekker T, Van den Heuvel-Panhuizen M, de Lange J, Wijers M (2007) Problem solving as a challenge for mathematics education in the Netherlands. ZDM Int J Math Educ 39(5–6):405–418

English LD, Gainsburg J (2016) Problem solving in a 21st-century mathematics curriculum. In: English LD, Kirshner D (eds) Handbook of international research in mathematics education. Routledge, New York, pp 313–335

Hadamard J (1945) An essay on the psychology of invention in the mathematical field. Dover Publications, New York

Halmos PR (1980) The heart of mathematics. Am Math Mon 87(7):519–524

Halmos PR (1994) What is teaching. Am Math Mon 101(9):848–854

Hilbert D (1902) Mathematical problems. Bulletin of the American Mathematical Society, 8:437–479

Hoyles C, Lagrange J-B (eds) (2010) Mathematics education and technology: rethinking the terrain. The 17th ICMI study. Springer, New York

Krutestkii VA (1976) The psychology of mathematical abilities in school children. University of Chicago Press, Chicago

Lester FK, Kehle PE (1994) From problem solving to modeling: The evolution of thinking about research on complex mathematical activity. In: Lesh R, Doerr HM (ed) Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching. Mahawah: New Jersey, pp 501–517

Lesh R, Zawojewski JS (2007) Problem solving and modeling. In: Lester FK Jr (ed) The second handbook of research on mathematics teaching and learning. National Council of Teachers of Mathematics. Information Age Publishing, Charlotte, pp 763–804

Lester F, Kehle PE (2003) From problem solving to modeling: the evolution of thinking about research on complex mathematical activity. In: Lesh R, Doerr H (eds) Beyond constructivism: models and modeling perspectives on mathematics problem solving, learning and teaching. Lawrence Erlbaum, Mahwah, pp 501–518

Liljedahl P, Santos-Trigo M (2019) Mathematical problem solving. Current themes, trends and research, https://doi.org/10.1007/978-3-030-10472-6 Cham, Switzerland: Springer

NCTM (1989) Curriculum and evaluation standards for school mathematics. NCTM, Reston

NCTM (2000) Principles and standards for school mathematics. National Council of Teachers of Mathematics, Reston

NCTM (2009) Focus in high school mathematics. Reasoning and sense making. NCTM, Reston

Perkins DN, Simmons R (1988) Patterns of misunderstanding: An integrative model of science, math, and programming. Rev of Edu Res 58(3):303–326

Polya G (1945) How to solve it. Princeton University Press, Princeton

Book   Google Scholar  

Santos-Trigo M (2007) Mathematical problem solving: an evolving research and practice domain. ZDM Int J Math Educ 39(5, 6):523–536

Santos-Trigo M, Reyes-Martínez I (2018) High school prospective teachers’ problem-solving reasoning that involves the coordinated use of digital technologies. Int J Math Educ Sci Technol. https://doi.org/10.1080/0020739X.2018.1489075

Santos-Trigo M, Reyes-Rodriguez, A (2016) The use of digital technology in finding multiple paths to solve and extend an equilateral triangle task, International. Journal of Mathematical Education in Science and Technology 47:1:58–81. https://doi.org/10.1080/0020739X.2015.1049228

Schoenfeld AH (1985) Mathematical problem solving. Academic, New York

Schoenfeld AH (1992) Learning to think mathematically: problem solving, metacognition, and sense making in mathematics. In: Grows DA (ed) Handbook of research on mathematics teaching and learning. Macmillan, New York, pp 334–370

Schoenfeld AH (2015) How we think: a theory of human decision-making, with a focus on teaching. In: Cho SJ (ed) The proceedings of the 12th international congress on mathematical education. Springer, Cham, pp 229–243. https://doi.org/10.1007/978-3-319-12688-3_16

Chapter   Google Scholar  

Selden J, Mason A, Selden A (1989) Can average calculus students solve nonroutine problems? J Math Behav 8:45–50

Wertheimer M (1945) Productive thinking. Harper, New York

Download references

Author information

Authors and affiliations.

Centre for Research and Advanced Studies, Mathematics Education Department, Cinvestav-IPN, Mexico City, Mexico

Manuel Santos-Trigo

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Manuel Santos-Trigo .

Editor information

Editors and affiliations.

Department of Education, Centre for Mathematics Education, London South Bank University, London, UK

Stephen Lerman

Section Editor information

Department of Science Teaching, The Weizmann Institute of Science, Rehovot, Israel

Ruhama Even

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this entry

Cite this entry.

Santos-Trigo, M. (2020). Problem-Solving in Mathematics Education. In: Lerman, S. (eds) Encyclopedia of Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-030-15789-0_129

Download citation

DOI : https://doi.org/10.1007/978-3-030-15789-0_129

Published : 23 February 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-15788-3

Online ISBN : 978-3-030-15789-0

eBook Packages : Education Reference Module Humanities and Social Sciences Reference Module Education

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

The home of mathematics education in New Zealand.

• Forgot password ?
• Teaching material
• Problem solving activities
• Problem Solving Information
• Problem Solving Strategies

Problem solving strategies

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

What are problem solving strategies?

Strategies are things that Pólya would have us choose in his second stage of problem solving and use in his third stage ( What is Problem Solving? ). In actual fact he called them heuristics . They are a collection of general approaches that might work for a number of problems. 

There are a number of common strategies that students of primary age can use to help them solve problems. We discuss below several that will be of value for problems on this website and in books on problem solving. 

Common Problem Solving Strategies

• Guess (includes guess and check, guess and improve)
• Act It Out (act it out and use equipment)
• Draw (this includes drawing pictures and diagrams)
• Make a List (includes making a table)
• Think (includes using skills you know already)

We have provided a copymaster for these strategies so that you can make posters and display them in your classroom. It consists of a page per strategy with space provided to insert the name of any problem that you come across that uses that particular strategy (Act it out, Draw, Guess, Make a List). This kind of poster provides good revision for students. 

An in-depth look at strategies                 

We now look at each of the following strategies and discuss them in some depth. You will see that each strategy we have in our list includes two or more subcategories.

• Guess and check is one of the simplest strategies. Anyone can guess an answer. If they can also check that the guess fits the conditions of the problem, then they have mastered guess and check. This is a strategy that would certainly work on the Farmyard problem described below but it could take a lot of time and a lot of computation. Because it is so simple, you may have difficulty weaning some students away from guess and check. As problems get more difficult, other strategies become more important and more effective. However, sometimes when students are completely stuck, guessing and checking will provide a useful way to start to explore a problem. Hopefully that exploration will lead to a more efficient strategy and then to a solution.
• Guess and improve is slightly more sophisticated than guess and check. The idea is that you use your first incorrect guess to make an improved next guess. You can see it in action in the Farmyard problem. In relatively straightforward problems like that, it is often fairly easy to see how to improve the last guess. In some problems though, where there are more variables, it may not be clear at first which way to change the guessing.  
• Young students especially, enjoy using Act it Out . Students themselves take the role of things in the problem. In the Farmyard problem, the students might take the role of the animals though it is unlikely that you would have 87 students in your class! But if there are not enough students you might be able to include a teddy or two. This is an effective strategy for demonstration purposes in front of the whole class. On the other hand, it can also be cumbersome when used by groups, especially if a largish number of students is involved.  Sometimes the students acting out the problem may get less out of the exercise than the students watching. This is because the participants are so engrossed in the mechanics of what they are doing that they don’t see the underlying mathematics. 
• Use Equipment is a strategy related to Act it Out. Generally speaking, any object that can be used in some way to represent the situation the students are trying to solve, is equipment. One of the difficulties with using equipment is keeping track of the solution. The students need to be encouraged to keep track of their working as they manipulate the equipment. Some students need to be encouraged and helped to use equipment. Many students seem to prefer to draw. This may be because it gives them a better representation of the problem in hand. Since there are problems where using equipment is a better strategy than drawing, you should encourage students' use of equipment by modelling its use yourself from time to time.  
• It is fairly clear that a picture has to be used in the strategy Draw a Picture . But the picture need not be too elaborate. It should only contain enough detail to help solve the problem. Hence a rough circle with two marks is quite sufficient for chickens and a blob plus four marks will do a pig. All students should be encouraged to use this strategy at some point because it helps them ‘see’ the problem and it can develop into quite a sophisticated strategy later.
• It’s hard to know where Drawing a Picture ends and Drawing a Diagram begins. You might think of a diagram as anything that you can draw which isn’t a picture. But where do you draw the line between a picture and a diagram? As you can see with the chickens and pigs, discussed above, regular picture drawing develops into drawing a diagram. Venn diagrams and tree diagrams are particular types of diagrams that we use so often they have been given names in their own right.  
• There are a number of ways of using Make a Table . These range from tables of numbers to help solve problems like the Farmyard, to the sort of tables with ticks and crosses that are often used in logic problems. Tables can also be an efficient way of finding number patterns.
• When an Organised List is being used, it should be arranged in such a way that there is some natural order implicit in its construction. For example, shopping lists are generally not organised. They usually grow haphazardly as you think of each item. A little thought might make them organised. Putting all the meat together, all the vegetables together, and all the drinks together, could do this for you. Even more organisation could be forced by putting all the meat items in alphabetical order, and so on. Someone we know lists the items on her list in the order that they appear on her route through the supermarket.  
• Being systematic may mean making a table or an organised list but it can also mean keeping your working in some order so that it is easy to follow when you have to go back over it. It means that you should work logically as you go along and make sure you don’t miss any steps in an argument. And it also means following an idea for a while to see where it leads, rather than jumping about all over the place chasing lots of possible ideas.
• It is very important to keep track of your work. We have seen several groups of students acting out a problem and having trouble at the end simply because they had not kept track of what they were doing. So keeping track is particularly important with Act it Out and Using Equipment. But it is important in many other situations too. Students have to know where they have been and where they are going or they will get hopelessly muddled. This begins to be more significant as the problems get more difficult and involve more and more steps.
• In many ways looking for patterns is what mathematics is all about. We want to know how things are connected and how things work and this is made easier if we can find patterns. Patterns make things easier because they tell us how a group of objects acts in the same way. Once we see a pattern we have much more control over what we are doing.
• Using symmetry helps us to reduce the difficulty level of a problem. Playing Noughts and crosses, for instance, you will have realised that there are three and not nine ways to put the first symbol down. This immediately reduces the number of possibilities for the game and makes it easier to analyse. This sort of argument comes up all the time and should be grabbed with glee when you see it.
• Finally working backwards is a standard strategy that only seems to have restricted use. However, it’s a powerful tool when it can be used. In the kind of problems we will be using in this web-site, it will be most often of value when we are looking at games. It frequently turns out to be worth looking at what happens at the end of a game and then work backward to the beginning, in order to see what moves are best.
• Then we come to use known skills .  This isn't usually listed in most lists of problem solving strategies but as we have gone through the problems in this web site, we have found it to be quite common.  The trick here is to see which skills that you know can be applied to the problem in hand. One example of this type is Fertiliser (Measurement, level 4).  In this problem, the problem solver has to know the formula for the area of a rectangle to be able to use the data of the problem.  This strategy is related to the first step of problem solving when the problem solver thinks 'have I seen a problem like this before?'  Being able to relate a word problem to some previously acquired skill is not easy but it is extremely important.

Uses of strategies                                           

Different strategies have different uses. We’ll illustrate this by means of a problem.

The Farmyard Problem : In the farmyard there are some pigs and some chickens. In fact there are 87 animals and 266 legs. How many pigs are there in the farmyard?

Some strategies help you to understand a problem. Let’s kick off with one of those. Guess and check . Let’s guess that there are 80 pigs. If there are they will account for 320 legs. Clearly we’ve over-guessed the number of pigs. So maybe there are only 60 pigs. Now 60 pigs would have 240 legs. That would leave us with 16 legs to be found from the chickens. It takes 8 chickens to produce 16 legs. But 60 pigs plus 8 chickens is only 68 animals so we have landed nearly 20 animals short.

Obviously we haven’t solved the problem yet but we have now come to grips with some of the important aspects of the problem. We know that there are 87 animals and so the number of pigs plus the number of chickens must add up to 87. We also know that we have to use the fact that pigs have four legs and chickens two, and that there have to be 266 legs altogether.

Some strategies are methods of solution in themselves. For instance, take Guess and improve . Supposed we guessed 60 pigs for a total of 240 legs. Now 60 pigs imply 27 chickens, and that gives another 54 legs. Altogether then we’d have 294 legs at this point.

Unfortunately we know that there are only 266 legs. So we’ve guessed too high. As pigs have more legs than hens, we need to reduce the guess of 60 pigs. How about reducing the number of pigs to 50? That means 37 chickens and so 200 + 74 = 274 legs.

We’re still too high. Now 40 pigs and 47 hens gives 160 + 94 = 254 legs. We’ve now got too few legs so we need to guess more pigs.

You should be able to see now how to oscillate backwards and forwards until you hit on the right number of pigs. So guess and improve is a method of solution that you can use on a number of problems.

Some strategies can give you an idea of how you might tackle a problem. Making a table illustrates this point. We’ll put a few values in and see what happens.

From the table we can see that every time we change the number of pigs by one, we change the number of legs by two. This means that in our last guess in the table, we are five pigs away from the right answer. Then there have to be 46 pigs.

Some strategies help us to see general patterns so that we can make conjectures. Some strategies help us to see how to justify conjectures. And some strategies do other jobs. We’ll develop these ideas on the uses of strategies as this web-site grows.

What strategies can be used at what levels?

In the work we have done over the last few years, it seems that students are able to tackle and use more strategies as they continue with problem solving. They are also able to use them to a deeper level. We have observed the following strategies being used in the stated Levels.

Levels 1 and 2

• Draw a picture
• Use equipment
• Guess and check

Levels 3 and 4

• Draw a diagram
• Guess and improve
• Make a table
• Make an organised list

It is important to say here that the research has not been exhaustive. Possibly younger students can effectively use other strategies. However, we feel confident that most students at a given Curriculum Level can use the strategies listed at that Level above. As problem solving becomes more common in primary schools, we would expect some of the more difficult strategies to come into use at lower Levels.

Strategies can develop in at least two ways. First students' ability to use strategies develops with experience and practice. We mentioned that above. Second, strategies themselves can become more abstract and complex. It’s this development that we want to discuss here with a few examples.

Not all students may follow this development precisely. Some students may skip various stages. Further, when a completely novel problem presents itself, students may revert to an earlier stage of a strategy during the solution of the problem.

Draw: Earlier on we talked about drawing a picture and drawing a diagram. Students often start out by giving a very precise representation of the problem in hand. As they see that it is not necessary to add all the detail or colour, their pictures become more symbolic and only the essential features are retained. Hence we get a blob for a pig’s body and four short lines for its legs. Then students seem to realise that relationships between objects can be demonstrated by line drawings. The objects may be reduced to dots or letters. More precise diagrams may be required in geometrical problems but diagrams are useful in a great many problems with no geometrical content.

The simple "draw a picture" eventually develops into a wide variety of drawings that enable students, and adults, to solve a vast array of problems.

Guess: Moving from guess and check to guess and improve, is an obvious development of a simple strategy. Guess and check may work well in some problems but guess and improve is a simple development of guess and check.

But guess and check can develop into a sophisticated procedure that 5-year-old students couldn’t begin to recognise. At a higher level, but still in the primary school, students are able to guess patterns from data they have been given or they produce themselves. If they are to be sure that their guess is correct, then they have to justify the pattern in some way. This is just another way of checking.

All research mathematicians use guess and check. Their guesses are called "conjectures". Their checks are "proofs". A checked guess becomes a "theorem". Problem solving is very close to mathematical research. The way that research mathematicians work is precisely the Pólya four stage method ( What is Problem Solving? ). The only difference between problem solving and research is that in school, someone (the teacher) knows the solution to the problem. In research no one knows the solution, so checking solutions becomes more important.

So you see that a very simple strategy like guess and check can develop to a very deep level.

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India
• May 8, 2024   •   28:28 A Plan to Remake the Middle East
• May 7, 2024   •   27:43 How Changing Ocean Temperatures Could Upend Life on Earth
• May 6, 2024   •   29:23 R.F.K. Jr.’s Battle to Get on the Ballot
• May 3, 2024   •   25:33 The Protesters and the President
• May 2, 2024   •   29:13 Biden Loosens Up on Weed
• May 1, 2024   •   35:16 The New Abortion Fight Before the Supreme Court
• April 30, 2024   •   27:40 The Secret Push That Could Ban TikTok
• April 29, 2024   •   47:53 Trump 2.0: What a Second Trump Presidency Would Bring
• April 26, 2024   •   21:50 Harvey Weinstein Conviction Thrown Out
• April 25, 2024   •   40:33 The Crackdown on Student Protesters

Stormy Daniels Takes the Stand

The porn star testified for eight hours at donald trump’s hush-money trial. this is how it went..

Hosted by Michael Barbaro

Featuring Jonah E. Bromwich

Produced by Olivia Natt and Michael Simon Johnson

Edited by Lexie Diao

With Paige Cowett

Original music by Will Reid and Marion Lozano

Engineered by Alyssa Moxley

Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube

This episode contains descriptions of an alleged sexual liaison.

What happened when Stormy Daniels took the stand for eight hours in the first criminal trial of former President Donald J. Trump?

Jonah Bromwich, one of the lead reporters covering the trial for The Times, was in the room.

On today’s episode

Jonah E. Bromwich , who covers criminal justice in New York for The New York Times.

Background reading

In a second day of cross-examination, Stormy Daniels resisted the implication she had tried to shake down Donald J. Trump by selling her story of a sexual liaison.

Here are six takeaways from Ms. Daniels’s earlier testimony.

There are a lot of ways to listen to The Daily. Here’s how.

We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.

The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Dan Farrell, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.

Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Renan Borelli, Maddy Masiello, Isabella Anderson and Nina Lassam.

Jonah E. Bromwich covers criminal justice in New York, with a focus on the Manhattan district attorney’s office and state criminal courts in Manhattan. More about Jonah E. Bromwich

Advertisement