problem solving involving motion

Algebra Motion Problems

In these lessons, we will learn how to solve algebra word problems that involve motion.

Related Pages Rate, Time and Distance Word Problems Rate, Time and Distance More Algebra Word Problems More Algebra Lessons

What are Motion or Distance Word Problems? Motion problems are based on the formula

where d = distance, r = rate and t = time.

How to solve Motion or Distance Word Problems? Step 1: Draw a diagram to represent the relationship between the distances involved in the problem. Step 2: Set up a chart based on the formula: rate × time = distance. Step 3: Use the chart to set up one or more equations. Step 4: Solve the equations.

We will look at three types of Motion Word Problems:

• Two objects going in opposite directions.
• Both objects going in the same direction, but one goes further.
• One object going and returning at different rates.

Solve Motion Word Problems: Two objects going in opposite directions

Example: John and Philip who live 14 miles apart start at noon to walk toward each other at rates of 3 mph and 4 mph respectively. After how many hours will they meet?

Solution: Let x = time walked.

3x + 4x = 14 7x = 14 x = 2

They will meet in 2 hours.

How to solve motion word problems with objects traveling in opposite directions?

Example: Two cars leave from the same place at the same time and travel in opposite direction. One car travels at 55 mph and the other at 75 mph. After how many hours will there be 520 miles apart?

Example: Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?

Solve Motion Word Problems: Two objects going in the same direction

Example: Aaron left L.A. to drive at 55 mph towards Las Vegas. Mike left L.A. an hour after Aaron (also towards Las Vegas), driving at 70 mph. How long will it take Mike to overtake Aaron?

How to solve motion word problems with objects traveling in the same direction?

Example: John left his house at 3.00 pm to drive 60 mph to drive towards Michigan. Phoebe left the same house at 5.00 pm, driving 80 mph in the same direction as John. How long will it take Phoebe to overtake John?

Solve Motion Word Problems: One object going and returning at different rates

Example: In still water, Peter’s boat goes 4 times as fast as the current in the river. He takes a 15-mile trip up the river and returns in 4 hours. Find the rate of the current.

Solution: Let x = rate of the current.

The rate of the current is 2 mph.

Example: Gordon rode his bike at 15 mph to get his car. He then drove back at 45 mph. If the entire trip took him 8 hours, how far away was his car?

Motion Word Problems This is how to set up motion problems for Algebra. Three Types of Problems

• Both going the same direction but one going further
• Two going in opposite directions
• Going in one direction and then returning at a different rate.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Study Guides
• Motion Problems
• Preliminaries
• Quiz: Preliminaries
• Properties of Basic Mathematical Operations
• Quiz: Properties of Basic Mathematical Operations
• Multiplying and Dividing Using Zero
• Quiz: Multiplying and Dividing Using Zero
• Powers and Exponents
• Quiz: Powers and Exponents
• Square Roots and Cube Roots
• Quiz: Square Roots and Cube Roots
• Grouping Symbols
• Quiz: Grouping Symbols
• Divisibility Rules
• Quiz: Divisibility Rules
• Signed Numbers (Positive Numbers and Negative Numbers)
• Quiz: Signed Numbers (Positive Numbers and Negative Numbers)
• Quiz: Fractions
• Simplifying Fractions and Complex Fractions
• Quiz: Simplifying Fractions and Complex Fractions
• Quiz: Decimals
• Quiz: Percent
• Scientific Notation
• Quiz: Scientific Notation
• Quiz: Set Theory
• Variables and Algebraic Expressions
• Quiz: Variables and Algebraic Expressions
• Evaluating Expressions
• Quiz: Evaluating Expressions
• Quiz: Equations
• Ratios and Proportions
• Quiz: Ratios and Proportions
• Solving Systems of Equations (Simultaneous Equations)
• Quiz: Solving Systems of Equations (Simultaneous Equations)
• Quiz: Monomials
• Polynomials
• Quiz: Polynomials
• Quiz: Factoring
• What Are Algebraic Fractions?
• Operations with Algebraic Fractions
• Quiz: Operations with Algebraic Fractions
• Inequalities
• Quiz: Inequalities
• Graphing on a Number Line
• Quiz: Graphing on a Number Line
• Absolute Value
• Quiz: Absolute Value
• Solving Equations Containing Absolute Value
• Coordinate Graphs
• Quiz: Coordinate Graphs
• Linear Inequalities and Half-Planes
• Quiz: Linear Inequalities and Half-Planes
• Quiz: Functions
• Quiz: Variations
• Introduction to Roots and Radicals
• Simplifying Square Roots
• Quiz: Simplifying Square Roots
• Operations with Square Roots
• Quiz: Operations with Square Roots
• Solving Quadratic Equations
• Quiz: Solving Quadratic Equations
• Solving Technique
• Key Words and Phrases
• Simple Interest
• Compound Interest
• Ratio and Proportion
• Percent Change
• Number Problems
• Age Problems
• Coin Problems
• Mixture Problems
• Work Problems
• Number Problems with Two Variables
• Quiz: Word Problems

Here are some examples for solving motion problems.

How long will it take a bus traveling 72 km/hr to go 36 kms?

First circle what you're trying to find— how long will it take (time). Motion problems are solved by using the equation

Therefore, simply plug in: 72 km/hr is the rate (or speed) of the bus, and 36 km is the distance.

Therefore, it will take one‐half hour for the bus to travel 36 km at 72 km/hr.

How fast in miles per hour must a car travel to go 600 miles in 15 hours?

First, circle what you must find— how fast (rate). Now, using the equation d = rt , simply plug in 600 for distance and 15 for time.

So, the rate is 40 miles per hour.

Mrs. Benevides leaves Burbank at 9 a.m. and drives west on the Ventura Freeway at an average speed of 50 miles per hour. Ms. Twill leaves Burbank at 9:30 a.m. and drives west on the Ventura Freeway at an average speed of 60 miles per hour. At what time will Ms. Twill overtake Mrs. Benevides, and how many miles will they each have gone?

Because each travels the same distance,

Ms. Twill overtakes Mrs. Benevides after 2.5 hours of driving. The exact time can be figured out by using Ms. Twill's starting time: 9:30 + 2:30 = 12 noon. Since Ms. Twill has traveled for 2.5 hours at 60 mph, she has traveled 2.5 × 60, which is 150 miles. So, Mrs. Benevides is overtaken at 12 noon, and each has traveled 150 miles.

Previous Age Problems

Next Coin Problems

• Online Quizzes for CliffsNotes Algebra I Quick Review, 2nd Edition

5.3 Projectile Motion

Section learning objectives.

By the end of this section, you will be able to do the following:

• Describe the properties of projectile motion
• Apply kinematic equations and vectors to solve problems involving projectile motion

Teacher Support

The learning objectives in this section will help your students master the following standards:

• (C) analyze and describe accelerated motion in two dimensions using equations.

In addition, the High School Physics Laboratory Manual addresses content in this section in the lab titled: Motion in Two Dimensions, as well as the following standards:

• (C) analyze and describe accelerated motion in two dimensions using equations, including projectile and circular examples.

Section Key Terms

Properties of projectile motion.

Projectile motion is the motion of an object thrown (projected) into the air when, after the initial force that launches the object, air resistance is negligible and the only other force that object experiences is the force of gravity. The object is called a projectile , and its path is called its trajectory . Air resistance is a frictional force that slows its motion and can significantly alter the trajectory of the motion. Due to the difficulty in calculation, only situations in which the deviation from projectile motion is negligible and air resistance can be ignored are considered in introductory physics. That approximation is often quite accurate.

[BL] [OL] Review addition of vectors graphically and analytically.

[BL] [OL] [AL] Explain the term projectile motion. Ask students to guess what the motion of a projectile might depend on? Is the initial velocity important? Is the angle important? How will these things affect its height and the distance it covers? Introduce the concept of air resistance. Review kinematic equations.

The most important concept in projectile motion is that when air resistance is ignored, horizontal and vertical motions are independent , meaning that they don’t influence one another. Figure 5.27 compares a cannonball in free fall (in blue) to a cannonball launched horizontally in projectile motion (in red). You can see that the cannonball in free fall falls at the same rate as the cannonball in projectile motion. Keep in mind that if the cannon launched the ball with any vertical component to the velocity, the vertical displacements would not line up perfectly.

Since vertical and horizontal motions are independent, we can analyze them separately, along perpendicular axes. To do this, we separate projectile motion into the two components of its motion, one along the horizontal axis and the other along the vertical.

We’ll call the horizontal axis the x -axis and the vertical axis the y -axis. For notation, d is the total displacement, and x and y are its components along the horizontal and vertical axes. The magnitudes of these vectors are x and y , as illustrated in Figure 5.28 .

As usual, we use velocity, acceleration, and displacement to describe motion. We must also find the components of these variables along the x - and y -axes. The components of acceleration are then very simple a y = – g = –9.80 m/s 2 . Note that this definition defines the upwards direction as positive. Because gravity is vertical, a x = 0. Both accelerations are constant, so we can use the kinematic equations. For review, the kinematic equations from a previous chapter are summarized in Table 5.1 .

Where x is position, x 0 is initial position, v is velocity, v avg is average velocity, t is time and a is acceleration.

Solve Problems Involving Projectile Motion

The following steps are used to analyze projectile motion:

• Separate the motion into horizontal and vertical components along the x- and y-axes. These axes are perpendicular, so A x = A cos θ A x = A cos θ and A y = A sin θ A y = A sin θ are used. The magnitudes of the displacement s s along x- and y-axes are called x x and y . y . The magnitudes of the components of the velocity v v are v x = v ​ ​ ​ cos θ v x = v ​ ​ ​ cos θ and v y = v ​ ​ ​ sin θ v y = v ​ ​ ​ sin θ , where v v is the magnitude of the velocity and θ θ is its direction. Initial values are denoted with a subscript 0.
• Treat the motion as two independent one-dimensional motions, one horizontal and the other vertical. The kinematic equations for horizontal and vertical motion take the following forms Horizontal Motion ( a x = 0 ) x = x 0 + v x t v x = v 0 x = v x = velocity  is a constant. Horizontal Motion ( a x = 0 ) x = x 0 + v x t v x = v 0 x = v x = velocity  is a constant. Vertical motion (assuming positive is up a y = − g = − 9.80  m/s 2 a y = − g = − 9.80  m/s 2 ) y = y 0 + 1 2 ( v 0 y + v y ) t v y = v 0 y − g t y = y 0 + v 0 y t − 1 2 g t 2 v y 2 = v 0 y 2 − 2 g ( y − y 0 ) y = y 0 + 1 2 ( v 0 y + v y ) t v y = v 0 y − g t y = y 0 + v 0 y t − 1 2 g t 2 v y 2 = v 0 y 2 − 2 g ( y − y 0 )
• Solve for the unknowns in the two separate motions (one horizontal and one vertical). Note that the only common variable between the motions is time t t . The problem solving procedures here are the same as for one-dimensional kinematics.

Teacher Demonstration

Demonstrate the path of a projectile by doing a simple demonstration. Toss a dark beanbag in front of a white board so that students can get a good look at the projectile path. Vary the toss angles, so different paths can be displayed. This demonstration could be extended by using digital photography. Draw a reference grid on the whiteboard, then toss the bag at different angles while taking a video. Replay this in slow motion to observe and compare the altitudes and trajectories.

Tips For Success

For problems of projectile motion, it is important to set up a coordinate system. The first step is to choose an initial position for x x and y y . Usually, it is simplest to set the initial position of the object so that x 0 = 0 x 0 = 0 and y 0 = 0 y 0 = 0 .

Watch Physics

Projectile at an angle.

This video presents an example of finding the displacement (or range) of a projectile launched at an angle. It also reviews basic trigonometry for finding the sine, cosine and tangent of an angle.

• The time to reach the ground would remain the same since the vertical component is unchanged.
• The time to reach the ground would remain the same since the vertical component of the velocity also gets doubled.
• The time to reach the ground would be halved since the horizontal component of the velocity is doubled.
• The time to reach the ground would be doubled since the horizontal component of the velocity is doubled.

Worked Example

A fireworks projectile explodes high and away.

During a fireworks display like the one illustrated in Figure 5.30 , a shell is shot into the air with an initial speed of 70.0 m/s at an angle of 75° above the horizontal. The fuse is timed to ignite the shell just as it reaches its highest point above the ground. (a) Calculate the height at which the shell explodes. (b) How much time passed between the launch of the shell and the explosion? (c) What is the horizontal displacement of the shell when it explodes?

The motion can be broken into horizontal and vertical motions in which a x = 0 a x = 0 and   a y = g   a y = g . We can then define x 0 x 0 and y 0 y 0 to be zero and solve for the maximum height .

By height we mean the altitude or vertical position y y above the starting point. The highest point in any trajectory, the maximum height, is reached when   v y = 0   v y = 0 ; this is the moment when the vertical velocity switches from positive (upwards) to negative (downwards). Since we know the initial velocity, initial position, and the value of v y when the firework reaches its maximum height, we use the following equation to find y y

Because y 0 y 0 and v y v y are both zero, the equation simplifies to

Solving for y y gives

Now we must find v 0 y v 0 y , the component of the initial velocity in the y -direction. It is given by v 0 y = v 0 sin θ v 0 y = v 0 sin θ , where v 0 y v 0 y is the initial velocity of 70.0 m/s, and θ = 75 ∘ θ = 75 ∘ is the initial angle. Thus,

Since up is positive, the initial velocity and maximum height are positive, but the acceleration due to gravity is negative. The maximum height depends only on the vertical component of the initial velocity. The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding.

There is more than one way to solve for the time to the highest point. In this case, the easiest method is to use y = y 0 + 1 2 ( v 0 y + v y ) t y = y 0 + 1 2 ( v 0 y + v y ) t . Because y 0 y 0 is zero, this equation reduces to

Note that the final vertical velocity, v y v y , at the highest point is zero. Therefore,

This time is also reasonable for large fireworks. When you are able to see the launch of fireworks, you will notice several seconds pass before the shell explodes. Another way of finding the time is by using y = y 0 + v 0 y t − 1 2 g t 2 y = y 0 + v 0 y t − 1 2 g t 2 , and solving the quadratic equation for t t .

Because air resistance is negligible, a x = 0 a x = 0 and the horizontal velocity is constant. The horizontal displacement is horizontal velocity multiplied by time as given by x = x 0 + v x t x = x 0 + v x t , where x 0 x 0 is equal to zero

where v x v x is the x -component of the velocity, which is given by v x = v 0 cos θ 0 . v x = v 0 cos θ 0 . Now,

The time t t for both motions is the same, and so x x is

The horizontal motion is a constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping the fireworks fragments from falling on spectators. Once the shell explodes, air resistance has a major effect, and many fragments will land directly below, while some of the fragments may now have a velocity in the –x direction due to the forces of the explosion.

[BL] [OL] [AL] Talk about the sample problem. Discuss the variables or unknowns in each part of the problem Ask students which kinematic equations may be best suited to solve the different parts of the problem.

The expression we found for y y while solving part (a) of the previous problem works for any projectile motion problem where air resistance is negligible. Call the maximum height y = h y = h ; then,

This equation defines the maximum height of a projectile . The maximum height depends only on the vertical component of the initial velocity.

Calculating Projectile Motion: Hot Rock Projectile

Suppose a large rock is ejected from a volcano, as illustrated in Figure 5.31 , with a speed of 25.0   m / s 25.0   m / s and at an angle 3 5 ° 3 5 ° above the horizontal. The rock strikes the side of the volcano at an altitude 20.0 m lower than its starting point. (a) Calculate the time it takes the rock to follow this path.

Breaking this two-dimensional motion into two independent one-dimensional motions will allow us to solve for the time. The time a projectile is in the air depends only on its vertical motion.

While the rock is in the air, it rises and then falls to a final position 20.0 m lower than its starting altitude. We can find the time for this by using

If we take the initial position y 0 y 0 to be zero, then the final position is y = − 20.0  m . y = − 20.0  m . Now the initial vertical velocity is the vertical component of the initial velocity, found from

Substituting known values yields

Rearranging terms gives a quadratic equation in t t

This expression is a quadratic equation of the form a t 2 + b t + c = 0 a t 2 + b t + c = 0 , where the constants are a = 4.90, b = –14.3, and c = –20.0. Its solutions are given by the quadratic formula

This equation yields two solutions t = 3.96 and t = –1.03. You may verify these solutions as an exercise. The time is t = 3.96 s or –1.03 s. The negative value of time implies an event before the start of motion, so we discard it. Therefore,

The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 m / s 14.3 m / s and lands 20.0 m below its starting altitude will spend 3.96 s in the air.

Practice Problems

The fact that vertical and horizontal motions are independent of each other lets us predict the range of a projectile. The range is the horizontal distance R traveled by a projectile on level ground, as illustrated in Figure 5.32 . Throughout history, people have been interested in finding the range of projectiles for practical purposes, such as aiming cannons.

How does the initial velocity of a projectile affect its range? Obviously, the greater the initial speed v 0 v 0 , the greater the range, as shown in the figure above. The initial angle θ 0 θ 0 also has a dramatic effect on the range. When air resistance is negligible, the range R R of a projectile on level ground is

where v 0 v 0 is the initial speed and θ 0 θ 0 is the initial angle relative to the horizontal. It is important to note that the range doesn’t apply to problems where the initial and final y position are different, or to cases where the object is launched perfectly horizontally.

Virtual Physics

Projectile motion.

In this simulation you will learn about projectile motion by blasting objects out of a cannon. You can choose between objects such as a tank shell, a golf ball or even a Buick. Experiment with changing the angle, initial speed, and mass, and adding in air resistance. Make a game out of this simulation by trying to hit the target.

Check Your Understanding

• Projectile motion is the motion of an object projected into the air and moving under the influence of gravity.
• Projectile motion is the motion of an object projected into the air and moving independently of gravity.
• Projectile motion is the motion of an object projected vertically upward into the air and moving under the influence of gravity.
• Projectile motion is the motion of an object projected horizontally into the air and moving independently of gravity.

What is the force experienced by a projectile after the initial force that launched it into the air in the absence of air resistance?

• The nuclear force
• The gravitational force
• The electromagnetic force
• The contact force

Use the Check Your Understanding questions to assess whether students achieve the learning objectives for this section. If students are struggling with a specific objective, the Check Your Understanding will help identify which objective is causing the problem and direct students to the relevant content.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: Physics
• Publication date: Mar 26, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/physics/pages/1-introduction
• Section URL: https://openstax.org/books/physics/pages/5-3-projectile-motion

© Jan 19, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Physics Problems with Solutions

Motion problems, questions with solutions and tutorials.

Free questions and problems related to the SAT test and tutorials on rectilinear motion with either uniform velocity or uniform acceleration are included. The concepts of displacement, distance, velocity, speed, acceleration are thoroughly discussed. Problems, questions and examples are presented with solutions and detailed explanations. Graphical analysis of motion problems are also included.

Projectile Equations, Problems and Solutions

• Projectile Problems with Solutions and Explanations
• Solutions and Explanations to Projectile Problems
• Projectile Equations with Explanations

Distance and Displacement

• Displacement and Distance: Tutorials with Examples
• Displacement and Distance: Problems with Solutions

Velocity and Speed

• Velocity and Speed: Tutorials with Examples
• Velocity and Speed: Problems with Solutions

Uniform Acceleration

• Acceleration: Tutorials with Examples
• Uniform Acceleration Motion: Problems with Solutions
• Uniform Acceleration Motion: Equations with Explanations

Graphical Analysis of Motion

• Free SAT II Physics Practice Questions with Solutions on Graphical Analysis of Motion with detailed solutions

Formulas and Constants

• Physics Formulas Reference
• SI Prefixes Used with Units in Physics, Chemistry and Engineering
• Constants in Physics, Chemistry and Engineering

Popular Pages

• Privacy Policy

Dynamics: Force and Newton’s Laws of Motion

Problem-solving strategies, learning objective.

By the end of this section, you will be able to:

• Understand and apply a problem-solving procedure to solve problems using Newton’s laws of motion.

Success in problem solving is obviously necessary to understand and apply physical principles, not to mention the more immediate need of passing exams. The basics of problem solving, presented earlier in this text, are followed here, but specific strategies useful in applying Newton’s laws of motion are emphasized. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, and so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy for Newton’s Laws of Motion

Step 1. As usual, it is first necessary to identify the physical principles involved. Once it is determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation . Such a sketch is shown in Figure 1(a). Then, as in Figure 1(b), use arrows to represent all forces, label them carefully, and make their lengths and directions correspond to the forces they represent (whenever sufficient information exists).

Figure 1. (a) A sketch of Tarzan hanging from a vine. (b) Arrows are used to represent all forces. T is the tension in the vine above Tarzan, F T is the force he exerts on the vine, and w is his weight. All other forces, such as the nudge of a breeze, are assumed negligible. (c) Suppose we are given the ape man’s mass and asked to find the tension in the vine. We then define the system of interest as shown and draw a free-body diagram. F T is no longer shown, because it is not a force acting on the system of interest; rather, F T  acts on the outside world. (d) Showing only the arrows, the head-to-tail method of addition is used. It is apparent that T = –w , if Tarzan is stationary.

Step 2. Identify what needs to be determined and what is known or can be inferred from the problem as stated. That is, make a list of knowns and unknowns. Then carefully determine the system of interest . This decision is a crucial step, since Newton’s second law involves only external forces. Once the system of interest has been identified, it becomes possible to determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure 1(c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated earlier in this chapter, the system of interest depends on what question we need to answer. This choice becomes easier with practice, eventually developing into an almost unconscious process. Skill in clearly defining systems will be beneficial in later chapters as well.

A diagram showing the system of interest and all of the external forces is called a free-body diagram . Only forces are shown on free-body diagrams, not acceleration or velocity. We have drawn several of these in worked examples. Figure 1(c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Step 3. Once a free-body diagram is drawn, Newton’s second law can be applied to solve the problem . This is done in Figure 1(d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then they add like scalars. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. This is done by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known.

Applying Newton’s Second Law

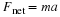
F net x  = ma ,

F net y = 0.

You will need this information in order to determine unknown forces acting in a system.

Step 4. As always, check the solution to see whether it is reasonable . In some cases, this is obvious. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving, and with experience it becomes progressively easier to judge whether an answer is reasonable. Another way to check your solution is to check the units. If you are solving for force and end up with units of m/s, then you have made a mistake.

Section Summary

To solve problems involving Newton’s laws of motion, follow the procedure described:

• Draw a sketch of the problem.
• Identify known and unknown quantities, and identify the system of interest. Draw a free-body diagram, which is a sketch showing all of the forces acting on an object. The object is represented by a dot, and the forces are represented by vectors extending in different directions from the dot. If vectors act in directions that are not horizontal or vertical, resolve the vectors into horizontal and vertical components and draw them on the free-body diagram.
• Write Newton’s second law in the horizontal and vertical directions and add the forces acting on the object. If the object does not accelerate in a particular direction (for example, the x-direction) then  F net x  = 0 . If the object does accelerate in that direction,  F net x  = ma .
• Check your answer. Is the answer reasonable? Are the units correct?

Problems & Exercises

1. A 5.00 × 10 5 -kg rocket is accelerating straight up. Its engines produce 1.250 × 10 7  of thrust, and air resistance is 4.50 × 10 6 N. What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

2. The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is 1.80 m/s 2 , what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.

3. Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

4. When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

5. A freight train consists of two 8.00 × 10 4   engines and 45 cars with average masses of 5.50 × 10 4 kg . (a) What force must each engine exert backward on the track to accelerate the train at a rate of 5.00 × 10 -2  if the force of friction is 7.50 × 10 5 , assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?

6. Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of 1.75 × 10 5  backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is 0.150 m/s 2 , what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.

7. A 1100-kg car pulls a boat on a trailer. (a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of 0.550 m/s 2 ? The mass of the boat plus trailer is 700 kg. (b) What is the force in the hitch between the car and the trailer if 80% of the resisting forces are experienced by the boat and trailer?

8. (a) Find the magnitudes of the forces F 1 and F 2  that add to give the total force F tot  shown in Figure 4. This may be done either graphically or by using trigonometry. (b) Show graphically that the same total force is obtained independent of the order of addition of   F 1 and F 2 . (c) Find the direction and magnitude of some other pair of vectors that add to give F tot . Draw these to scale on the same drawing used in part (b) or a similar picture.

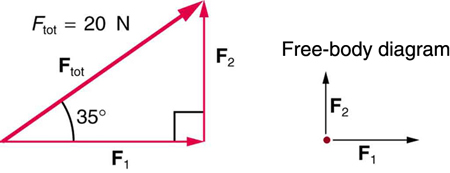
9. Two children pull a third child on a snow saucer sled exerting forces  F 1 and F 2 as shown from above in Figure 4 . Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of  F 1 and F 2 .

10. Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure 6 to pull it out. (a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is 2.00°? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. (b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to 7.00° and you still apply the force found in part (a) to its center?

11. What force is exerted on the tooth in Figure 7 if the tension in the wire is 25.0 N? Note that the force applied to the tooth is smaller than the tension in the wire, but this is necessitated by practical considerations of how force can be applied in the mouth. Explicitly show how you follow steps in the Problem-Solving Strategy for Newton’s laws of motion.

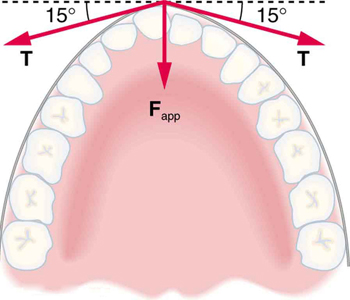
Figure 7. Braces are used to apply forces to teeth to realign them. Shown in this figure are the tensions applied by the wire to the protruding tooth. The total force applied to the tooth by the wire, F app , points straight toward the back of the mouth.

12. Figure 9 shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible. (a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope. (b) Find the tension in the rope above Superhero. (c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.

Figure 9. Superhero and Trusty Sidekick hang motionless on a rope as they try to figure out what to do next. Will the tension be the same everywhere in the rope?

13. A nurse pushes a cart by exerting a force on the handle at a downward angle 35.0º below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N. (a) Draw a free-body diagram for the system of interest. (b) What force must the nurse exert to move at a constant velocity?

14. Construct Your Own Problem Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.

15. Construct Your Own Problem Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children.

16. Unreasonable Results (a) Repeat Exercise 7, but assume an acceleration of 1.20 m/s 2  is produced. (b) What is unreasonable about the result? (c) Which premise is unreasonable, and why is it unreasonable?

17. Unreasonable Results (a) What is the initial acceleration of a rocket that has a mass of 1.50 × 10 6  at takeoff, the engines of which produce a thrust of 2.00 × 10 6 ? Do not neglect gravity. (b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.) (c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)

Selected Solutions to Problems & Exercises

1. Using the free-body diagram:

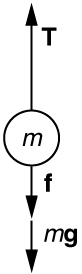
• [latex]{F}_{\text{net}}=T-f-mg=\text{ma}\\[/latex] ,

[latex]a=\frac{T-f-\text{mg}}{m}=\frac{1\text{.}\text{250}\times {\text{10}}^{7}\text{N}-4.50\times {\text{10}}^{\text{6}}N-\left(5.00\times {\text{10}}^{5}\text{kg}\right)\left(9.{\text{80 m/s}}^{2}\right)}{5.00\times {\text{10}}^{5}\text{kg}}=\text{6.20}{\text{m/s}}^{2}\\[/latex]

3. Use Newton’s laws of motion.

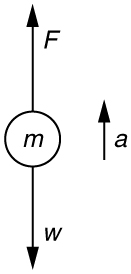
[latex]F=\left(\text{70.0 kg}\right)\left[\left(\text{39}\text{.}{\text{2 m/s}}^{2}\right)+\left(9\text{.}{\text{80 m/s}}^{2}\right)\right]\\[/latex] [latex]=3.\text{43}\times {\text{10}}^{3}\text{N}\\[/latex].  The force exerted by the high-jumper is actually down on the ground, but F is up from the ground and makes him jump.

• This result is reasonable, since it is quite possible for a person to exert a force of the magnitude of 10 3 N.

5. (a) 4.41 × 10 5 N (b) 1.50 × 10 5 N

7. (a) 910 N (b) 1.11 × 10 3

9. (a) a = 0.139 m/s, θ = 12.4º

11. Use Newton’s laws since we are looking for forces.

• Draw a free-body diagram:

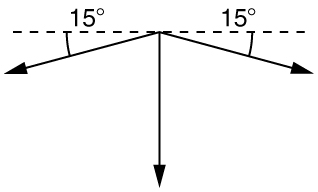
• The tension is given as T = 25.0 N. Find F app . Using Newton’s laws gives:[latex]\sigma{F}_{y}=0\\[/latex], so that applied force is due to the y -components of the two tensions: F app = 2 T  sin  θ  = 2(25.0 N) sin(15º) = 12.9 N The x -components of the tension cancel. [latex]\sum{F}_{x}=0\\[/latex].
• This seems reasonable, since the applied tensions should be greater than the force applied to the tooth.
• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.8: Applications and Variation

• Last updated
• Save as PDF
• Page ID 6442

Learning Objectives

• Solve applications involving uniform motion (distance problems).
• Solve work-rate applications.
• Set up and solve applications involving direct, inverse, and joint variation.

Solving Uniform Motion Problems

Uniform motion (or distance) 37 problems involve the formula \(D=rt\), where the distance \(D\) is given as the product of the average rate \(r\) and the time \(t\) traveled at that rate. If we divide both sides by the average rate \(r\), then we obtain the formula

\(t = \frac { D } { r }\)

For this reason, when the unknown quantity is time, the algebraic setup for distance problems often results in a rational equation. We begin any uniform motion problem by first organizing our data with a chart. Use this information to set up an algebraic equation that models the application.

Example \(\PageIndex{1}\):

Sally traveled \(15\) miles on the bus and then another \(72\) miles on a train. The train was \(18\) miles per hour faster than the bus, and the total trip took \(2\) hours. What was the average speed of the train?

First, identify the unknown quantity and organize the data.

Let \(x\) represent the average speed (in miles per hour) of the bus.

Let \(x+18\) represent the average speed of the train.

To avoid introducing two more variables for the time column, use the formula \(t=\frac{D}{r}\). The time for each leg of the trip is calculated as follows:

\(\begin{aligned} \color{Cerulean} { Time\: spent\: on\: the\: bus : }\color{black}{ t} = \frac { D } { r } & = \frac { 15 } { x } \\ \color{Cerulean} {Time\: spent\: on\: the\: train :}\color{black}{ t} = \frac { D } { r } & = \frac { 72 } { x + 18 } \end{aligned}\)

Use these expressions to complete the chart.

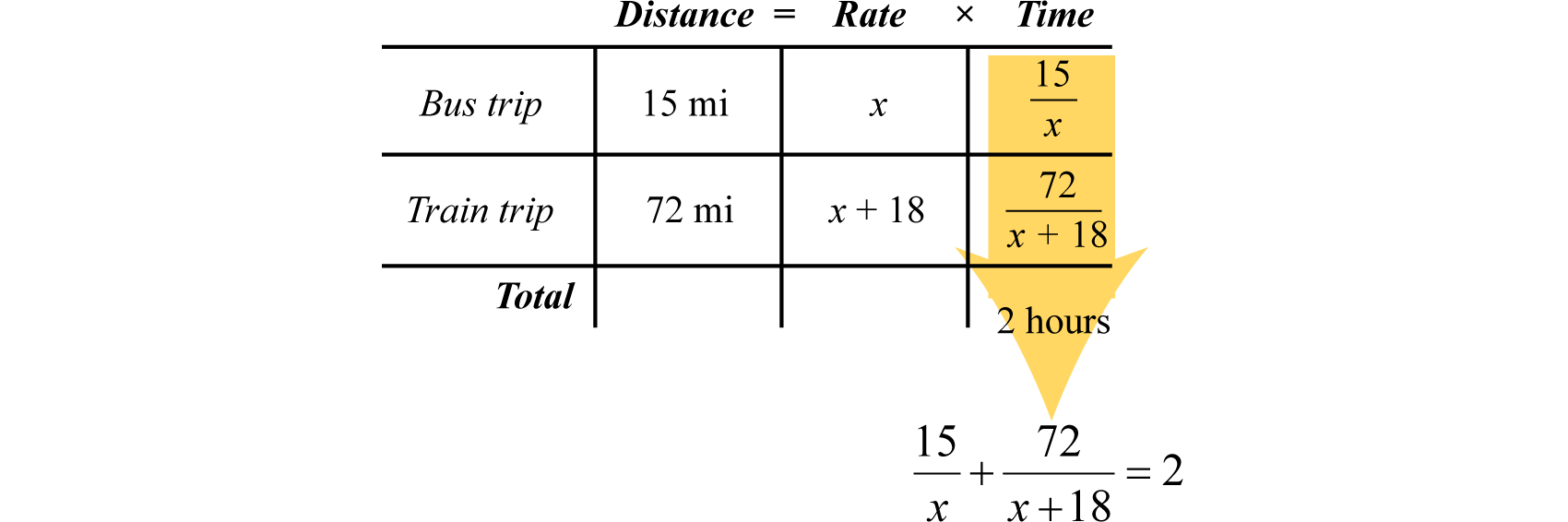
The algebraic setup is defined by the time column. Add the time spent on each leg of the trip to obtain a total of \(2\) hours:

We begin solving this equation by first multiplying both sides by the LCD, \(x(x+18)\).

\(\begin{aligned} \frac { 15 } { x } + \frac { 72 } { x + 18 } & = 2 \\ \color{Cerulean}{x ( x + 18 )}\color{black}{ \cdot} \left( \frac { 15 } { x } + \frac { 72 } { x + 18 } \right) & = \color{Cerulean}{x ( x + 18 )}\color{black}{ \cdot} 2 \\ \color{Cerulean}{x ( x + 18 )}\color{black}{ \cdot} \frac { 15 } { x } + \color{Cerulean}{x ( x + 18 )}\color{black}{ \cdot} \frac { 72 } { x + 18 } & = \color{Cerulean}{x ( x + 18 )}\color{black}{ \cdot} 2 \\ 15( x + 18 ) \cdot 72x & = 2x ( x + 18 ) \\ 15 x + 270 + 72 x & = 2 x ^ { 2 } + 36 x \\ 87 x + 270 & = 2 x ^ { 2 } + 36 x \\ 0 & = 2 x ^ { 2 } - 51 x - 270 \end{aligned}\)

Solve the resulting quadratic equation by factoring.

\(\begin{array} { l } { 0 = 2 x ^ { 2 } - 51 x - 270 } \\ { 0 = ( 2 x + 9 ) ( x - 30 ) } \end{array}\)

\(\begin{aligned} 2 x + 9 & = 0 \quad\quad \text { or } &x - 30 &= 0 \\ x &= - \frac { 9 } { 2 } & x& = 30 \end{aligned}\)

Since we are looking for an average speed we will disregard the negative answer and conclude the bus averaged \(30\) mph. Substitute \(x=30\) in the expression identified as the speed of the train.

\(x + 18 = 30 + 18 = 48\)

The speed of the train was \(48\) mph.

Example \(\PageIndex{2}\):

A boat can average \(12\) miles per hour in still water. On a trip downriver the boat was able to travel \(29\) miles with the current. On the return trip the boat was only able to travel \(19\) miles in the same amount of time against the current. What was the speed of the current?

First, identify the unknown quantities and organize the data.

Let \(c\) represent the speed of the river current.

Next, organize the given data in a chart. Traveling downstream, the current will increase the speed of the boat, so it adds to the average speed of the boat. Traveling upstream, the current slows the boat, so it will subtract from the average speed of the boat.

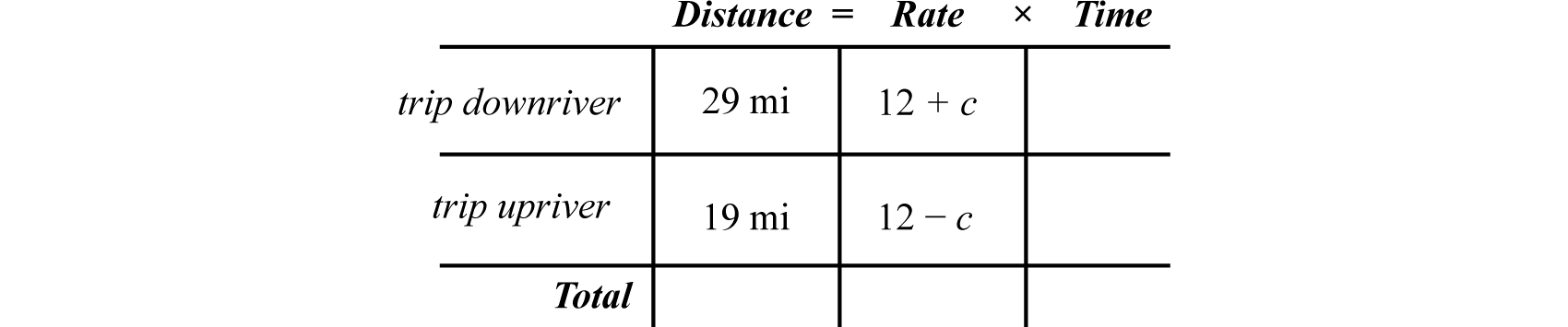
Use the formula \(t=\frac{D}{r}\) to fill in the time column.

\(\begin{aligned} \color{Cerulean} {trip\: downriver: } &\color{black}{ }t = \frac { D } { r } = \frac { 29 } { 12 + c } \\ \color{Cerulean} {trip\:upriver:} & \color{black}{t} = \frac { D } { r } = \frac { 19 } { 12 - c } \end{aligned}\)

Because the boat traveled the same amount of time downriver as it did upriver, finish the algebraic setup by setting the expressions that represent the times equal to each other.

\(\frac { 29 } { 12 + c } = \frac { 19 } { 12 - c }\)

Since there is a single algebraic fraction on each side, we can solve this equation using cross multiplication.

\(\begin{aligned} \frac { 29 } { 12 + c } & = \frac { 19 } { 12 - c } \\ 29 ( 12 - c ) & = 19 ( 12 + c ) \\ 348 - 29 c & = 228 + 19 c \\ 120 & = 48 c \\ \frac { 120 } { 48 } & = c \\ \frac { 5 } { 2 } & = c \end{aligned}\)

The speed of the current was \(2 \frac{1}{2}\) miles per hour.

Exercise \(\PageIndex{1}\)

A jet aircraft can average \(160\) miles per hour in calm air. On a trip, the aircraft traveled \(600\) miles with a tailwind and returned the \(600\) miles against a headwind of the same speed. If the total round trip took \(8\) hours, then what was the speed of the wind?

\(40\) miles per hour

www.youtube.com/v/0NglBthTwss

Solving Work-Rate Problems

The rate at which a task can be performed is called a work rate 38 . For example, if a painter can paint a room in \(6\) hours, then the task is to paint the room, and we can write

\(\frac { 1 \text { task } } { 6 \text { hours } } \quad \color{Cerulean}{work\:rate}\)

In other words, the painter can complete \(\frac{1}{6}\) of the task per hour. If he works for less than \(6\) hours, then he will perform a fraction of the task. If he works for more than \(6\) hours, then he can complete more than one task. For example,

\(\begin{aligned} \color{Cerulean}{work-rate \:\:\times\:\:time} &\color{black}{=} \color{Cerulean}{amount\:of\:task\:completed}\\ \frac { 1 } { 6 }\quad \times \quad3 h r s &= \:\frac { 1 } { 2 } \quad \color{Cerulean} { one-half\: of\: the\: room\: painted } \\ \frac { 1 } { 6 } \quad\times\quad 6 h r s &= \:1 \quad\color{Cerulean} { one\: whole\: room\: painted } \\ \frac { 1 } { 6 }\quad \times\:\: 12 \text { hrs } & = \:2\quad \color{Cerulean} { two\: whole\: rooms\: painted } \end{aligned}\)

Obtain the amount of the task completed by multiplying the work rate by the amount of time the painter works. Typically, work-rate problems involve people or machines working together to complete tasks. In general, if \(t\) represents the time two people work together, then we have the following work-rate formula 39 :

\(\frac { 1 } { t _ { 1 } } t + \frac { 1 } { t _ { 2 } } t =\color{Cerulean}{amount\:of\:task\:completed\:together}\)

Here \(\frac { 1 } { t _ { 1 } }\) and \(\frac { 1 } { t _ { 2 } }\) are the individual work rates.

Example \(\PageIndex{3}\):

Joe can paint a typical room in \(2\) hours less time than Mark. If Joe and Mark can paint \(5\) rooms working together in a \(12\) hour shift, how long does it take each to paint a single room?

Let \(x\) represent the time it takes Mark to paint a typical room.

Let \(x − 2\) represent the time it takes Joe to paint a typical room.

Therefore, Mark’s individual work-rate is \(\frac{1}{x}\) rooms per hour and Joe’s is \(\frac{1}{x−2}\) rooms per hour. Both men worked for \(12\) hours. We can organize the data in a chart, just as we did with distance problems.

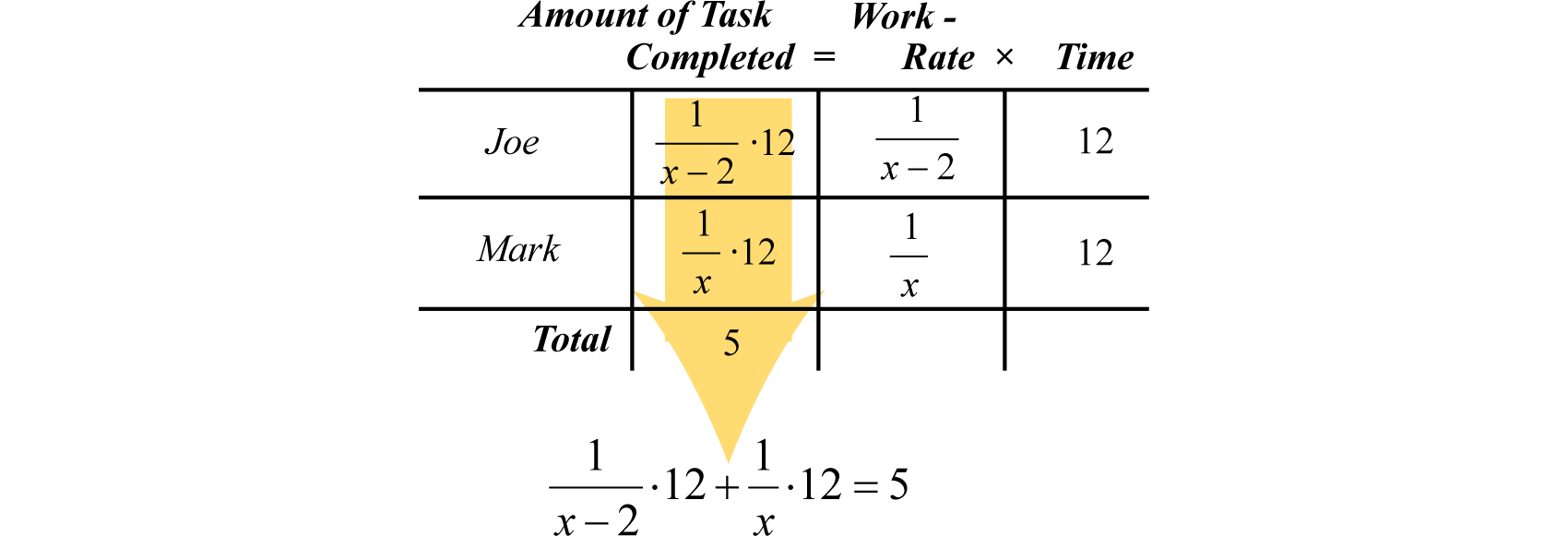
Working together, they can paint 5 total rooms in 12 hours. This leads us to the following algebraic setup:

\(\frac { 12 } { x - 2 } + \frac { 12 } { x } = 5\)

Multiply both sides by the LCD, \(x(x−2)\).

\(\begin{aligned} \color{Cerulean}{x ( x - 2 )}\color{black}{ \cdot} \left( \frac { 12 } { x - 2 } + \frac { 12 } { x } \right) & =\color{Cerulean}{ x ( x - 2 )}\color{black}{ \cdot} 5 \\ \color{Cerulean}{x ( x - 2 )}\color{black}{ \cdot} \frac { 12 } { x - 2 } + \color{Cerulean}{x ( x - 2 )}\color{black}{ \cdot} \frac { 12 } { x } & =\color{Cerulean}{ x ( x - 2 )}\color{black}{ \cdot} 5 \\ 12 x + 12 ( x - 2 ) & = 5 x ( x - 2 ) \\ 12 x + 12 x - 24 & = 5 x ^ { 2 } - 10 x \\ 0 & = 5 x ^ { 2 } - 34 x + 24 \end{aligned}\)

\(\begin{array} { l } { 0 = 5 x ^ { 2 } - 34 x + 24 } \\ { 0 = ( 5 x - 4 ) ( x - 6 ) } \end{array}\)

\(\begin{aligned} 5 x - 4 &= 0 \quad\quad \text { or } & x - 6& = 0 \\ 5 x &= 4 &x &= 6 \\ x& = \frac { 4 } { 5 } \end{aligned}\)

We can disregard \(\frac{4}{5}\) because back substituting into \(x − 2\) would yield a negative time to paint a room. Take \(x = 6\) to be the only solution and use it to find the time it takes Joe to paint a typical room.

\(x - 2 = 6 - 2 = 4\)

Joe can paint a typical room in \(4\) hours and Mark can paint a typical room in \(6\) hours. As a check we can multiply both work rates by \(12\) hours to see that together they can paint \(5\) rooms.

\(\left. \begin{array} { l } { \color{Cerulean} { Joe }\:\: \color{black}{\frac { 1 \text { room} } { 4 \text{hrs} }} \cdot 12 \text { hrs } = 3 \text { rooms } } \\ { \color{Cerulean} { Mark }\:\: \color{black}{\frac { 1 \text { room } } { 6 \text{hrs} }} \cdot 12 \text{hrs} = 2 \text { rooms } } \end{array} \right\} Total \:5\:rooms \:\color{Cerulean}{✓}\)

Example \(\PageIndex{4}\):

It takes Bill twice as long to lay a tile floor by himself as it does Manny. After working together with Bill for \(4\) hours, Manny was able to complete the job in \(2\) additional hours. How long would it have taken Manny working alone?

Let \(x\) represent the time it takes Manny to lay the floor alone.

Let \(2x\) represent the time it takes Bill to lay the floor alone.

Manny’s work rate is \(\frac{1}{x}\) of the floor per hour and Bill’s work rate is \(\frac{1}{2x}\). Bill worked on the job for \(4\) hours and Manny worked on the job for \(6\) hours.

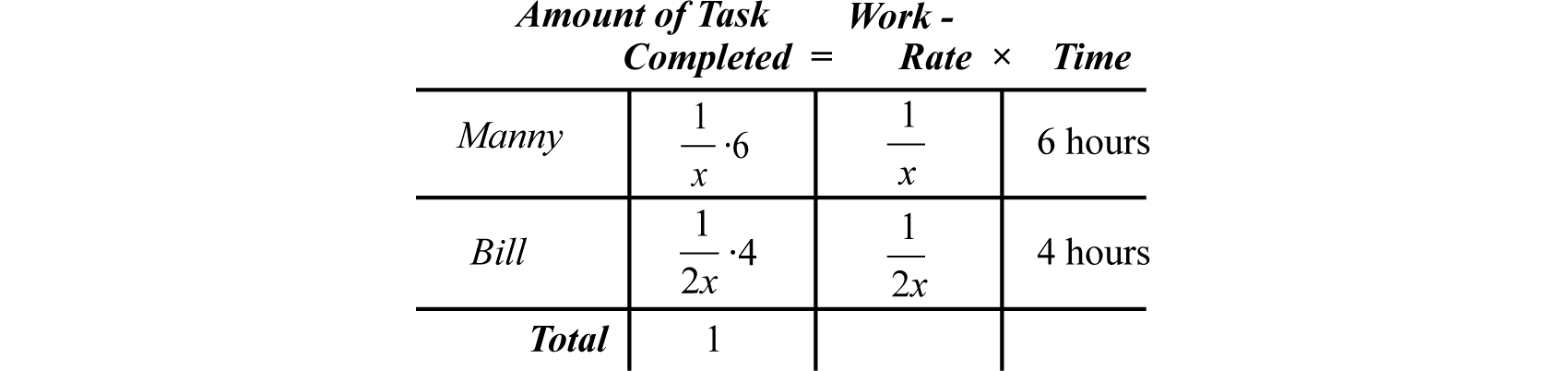
This leads us to the following algebraic setup:

\(\frac { 1 } { x } \cdot 6 + \frac { 1 } { 2 x } \cdot 4 = 1\)

\(\begin{aligned} \frac { 6 } { x } + \frac { 4 } { 2 x } & = 1 \\ \color{Cerulean}{x}\color{black}{ \cdot} \left( \frac { 6 } { x } + \frac { 2 } { x } \right) & = \color{Cerulean}{x}\color{black}{ \cdot} 1 \\ 6 + 2 & = x \\ 8 & = x \end{aligned}\)

It would have taken Manny \(8\) hours to complete the floor by himself.

Consider the work-rate formula where one task is to be completed.

\(\frac { 1 } { t _ { 1 } } t + \frac { 1 } { t _ { 2 } } t = 1\)

Factor out the time \(t\) and then divide both sides by \(t\). This will result in equivalent specialized work-rate formulas:

\(\begin{aligned} t \left( \frac { 1 } { t _ { 1 } } + \frac { 1 } { t _ { 2 } } \right) & = 1 \\ \frac { 1 } { t _ { 1 } } + \frac { 1 } { t _ { 2 } } & = \frac { 1 } { t } \end{aligned}\)

In summary, we have the following equivalent work-rate formulas:

\(\begin{array} { c } { \color{Cerulean} { Work \:rate\:formulas } } \\ { \frac { 1 } { t _ { 1 } } t + \frac { 1 } { t _ { 2 } } t = 1 \quad \text { or } \quad \frac { t } { t _ { 1 } } + \frac { t } { t _ { 2 } } = 1 \quad\text { or }\quad \frac { 1 } { t _ { 1 } } + \frac { 1 } { t _ { 2 } } = \frac { 1 } { t } } \end{array}\)

Exercise \(\PageIndex{2}\)

Matt can tile a countertop in \(2\) hours, and his assistant can do the same job in \(3\) hours. If Matt starts the job and his assistant joins him \(1\) hour later, then how long will it take to tile the countertop?

\(1 \frac{3}{5}\) hours

www.youtube.com/v/5g6sSFWGb7M

Solving Problems involving Direct, Inverse, and Joint variation

Many real-world problems encountered in the sciences involve two types of functional relationships. The first type can be explored using the fact that the distance \(s\) in feet an object falls from rest, without regard to air resistance, can be approximated using the following formula:

\(s=16t^{2}\)

Here \(t\) represents the time in seconds the object has been falling. For example, after \(2\) seconds the object will have fallen \(s = 16 ( 2 ) ^ { 2 } = 16 \cdot 4 = 64\) feet.

In this example, we can see that the distance varies over time as the product of a constant \(16\) and the square of the time \(t\). This relationship is described as direct variation 40 and \(16\) is called the constant of variation 41 . Furthermore, if we divide both sides of \(s=16t^{2}\) by \(t^{2}\) we have

\(\frac { s } { t ^ { 2 } } = 16\)

In this form, it is reasonable to say that \(s\) is proportional to \(t^{2}\), and \(16\) is called the constant of proportionality 42 . In general, we have

Here \(k\) is nonzero and is called the constant of variation or the constant of proportionality. Typically, we will be given information from which we can determine this constant.

Example \(\PageIndex{5}\):

An object’s weight on Earth varies directly to its weight on the Moon. If a man weighs \(180\) pounds on Earth, then he will weigh \(30\) pounds on the Moon. Set up an algebraic equation that expresses the weight on Earth in terms of the weight on the Moon and use it to determine the weight of a woman on the Moon if she weighs \(120\) pounds on Earth.

Let \(y\) represent weight on Earth.

Let \(x\) represent weight on the Moon.

We are given that the “weight on Earth varies directly to the weight on the Moon.”

To find the constant of variation \(k\), use the given information. A \(180\)-lb man on Earth weighs \(30\) pounds on the Moon, or \(y = 180\) when  \(x = 30\).

\(180 = k \cdot 30\)

Solve for \(k\).

\(\begin{array} { c } { \frac { 180 } { 30 } = k } \\ { 6 = k } \end{array}\)

Next, set up a formula that models the given information.

This implies that a person’s weight on Earth is \(6\) times his weight on the Moon. To answer the question, use the woman’s weight on Earth, \(y = 120\) lbs, and solve for \(x\).

\(\begin{array} { l } { 120 = 6 x } \\ { \frac { 120 } { 6 } = x } \\ { 20 = x } \end{array}\)

The woman weighs \(20\) pounds on the Moon.

The second functional relationship can be explored using the formula that relates the intensity of light \(I\) to the distance from its source \(d\).

\(I = \frac { k } { d ^ { 2 } }\)

Here \(k\) represents some constant. A foot-candle is a measurement of the intensity of light. One foot-candle is defined to be equal to the amount of illumination produced by a standard candle measured one foot away. For example, a \(125\)-Watt fluorescent growing light is advertised to produce \(525\) foot-candles of illumination. This means that at a distance \(d=1\) foot, \(I=525\) foot-candles and we have:

\(\begin{array} { l } { 525 = \frac { k } { ( 1 ) ^ { 2 } } } \\ { 525 = k } \end{array}\)

Using \(k=525\) we can construct a formula which gives the light intensity produced by the bulb:

\(I = \frac { 525 } { d ^ { 2 } }\)

Here \(d\) represents the distance the growing light is from the plants. In the following chart, we can see that the amount of illumination fades quickly as the distance from the plants increases.

This type of relationship is described as an inverse variation 44 . We say that I is inversely proportional 45 to the square of the distance \(d\) , where \(525\) is the constant of proportionality. In general, we have

Again, \(k\) is nonzero and is called the constant of variation or the constant of proportionality.

Example \(\PageIndex{6}\):

The weight of an object varies inversely as the square of its distance from the center of Earth. If an object weighs \(100\) pounds on the surface of Earth (approximately \(4,000\) miles from the center), how much will it weigh at \(1,000\) miles above Earth’s surface?

Let \(w\) represent the weight of the object.

Let \(d\) represent the object’s distance from the center of Earth.

Since “\(w\) varies inversely as the square of \(d\),” we can write

\(w = \frac { k } { d ^ { 2 } }\)

Use the given information to find \(k\). An object weighs \(100\) pounds on the surface of Earth, approximately \(4,000\) miles from the center. In other words, \(w = 100\) when \(d = 4,000\):

\(100 = \frac { k } { ( 4,000 ) ^ { 2 } }\)

\(\begin{aligned} \color{Cerulean}{( 4,000 ) ^ { 2 }}\color{black}{ \cdot} 100 & =\color{Cerulean}{ ( 4,000 ) ^ { 2 }}\color{black}{ \cdot} \frac { k } { ( 4,000 ) ^ { 2 } } \\ 1,600,000,000 &= k \\ 1.6 \times 10 ^ { 9 } &= k \end{aligned}\)

Therefore, we can model the problem with the following formula:

\(w = \frac { 1.6 \times 10 ^ { 9 } } { d ^ { 2 } }\)

To use the formula to find the weight, we need the distance from the center of Earth. Since the object is \(1,000\) miles above the surface, find the distance from the center of Earth by adding \(4,000\) miles:

\(d = 4,000 + 1,000 = 5,000 \:\:\text{miles}\)

To answer the question, use the formula with \(d = 5,000\).

\(\begin{aligned} y & = \frac { 1.6 \times 10 ^ { 9 } } { ( \color{OliveGreen}{5,000}\color{black}{ )} ^ { 2 } } \\ & = \frac { 1.6 \times 10 ^ { 9 } } { 25,000,000 } \\ & = \frac { 1.6 \times 10 ^ { 9 } } { 2.5 \times 10 ^ { 9 } } \\ & = 0.64 \times 10 ^ { 2 } \\ & = 64 \end{aligned}\)

The object will weigh \(64\) pounds at a distance \(1,000\) miles above the surface of Earth.

Lastly, we define relationships between multiple variables, described as joint variation 46 . In general, we have

Here \(k\) is nonzero and is called the constant of variation or the constant of proportionality.

Example \(\PageIndex{7}\):

The area of an ellipse varies jointly as \(a\), half of the ellipse’s major axis, and \(b\), half of the ellipse’s minor axis as pictured. If the area of an ellipse is \(300π cm^{2}\), where \(a=10\) cm and \(b=30\) cm, what is the constant of proportionality? Give a formula for the area of an ellipse.

If we let \(A\) represent the area of an ellipse, then we can use the statement “area varies jointly as \(a\) and \(b\)” to write

To find the constant of variation \(k\), use the fact that the area is \(300π\) when \(a=10\) and \(b=30\).

\(\begin{array} { c } { 300 \pi = k ( \color{OliveGreen}{10}\color{black}{ )} (\color{OliveGreen}{ 30}\color{black}{ )} } \\ { 300 \pi = 300 k } \\ { \pi = k } \end{array}\)

Therefore, the formula for the area of an ellipse is

\(A=πab\)

The constant of proportionality is \(π\) and the formula for the area of an ellipse is \(A=abπ\).

Exercise \(\PageIndex{3}\)

Given that \(y\) varies directly as the square of \(x\) and inversely with \(z\), where \(y=2\) when \(x=3\) and \(z=27\), find \(y\) when \(x=2\) and \(z=16\).

\(\frac{3}{2}\)

www.youtube.com/v/ee3AFf7b6Kg

Key Takeaways

• When solving distance problems where the time element is unknown, use the equivalent form of the uniform motion formula, \(t=\frac{D}{r}\), to avoid introducing more variables.
• When solving work-rate problems, multiply the individual work rate by the time to obtain the portion of the task completed. The sum of the portions of the task results in the total amount of work completed.
• The setup of variation problems usually requires multiple steps. First, identify the key words to set up an equation and then use the given information to find the constant of variation \(k\). After determining the constant of variation, write a formula that models the problem. Once a formula is found, use it to answer the question.

Exercise \(\PageIndex{4}\)

Use algebra to solve the following applications.

• Every morning Jim spends \(1\) hour exercising. He runs \(2\) miles and then he bikes \(16\) miles. If Jim can bike twice as fast as he can run, at what speed does he average on his bike?
• Sally runs \(3\) times as fast as she walks. She ran for \(\frac{3}{4}\) of a mile and then walked another \(3 \frac{1}{2}\) miles. The total workout took \(1 \frac{1}{2}\) hours. What was Sally’s average walking speed?
• On a business trip, an executive traveled \(720\) miles by jet and then another \(80\) miles by helicopter. If the jet averaged \(3\) times the speed of the helicopter, and the total trip took \(4\) hours, what was the average speed of the jet?
• A triathlete can run \(3\) times as fast as she can swim and bike \(6\) times as fast as she can swim. The race consists of a \(\frac{1}{4}\) mile swim, \(3\) mile run, and a \(12\) mile bike race. If she can complete all of these events in \(1 \frac{5}{8}\) hour, then how fast can she swim, run and bike?
• On a road trip, Marty was able to drive an average \(4\) miles per hour faster than George. If Marty was able to drive \(39\) miles in the same amount of time George drove \(36\) miles, what was Marty’s average speed?
• The bus is \(8\) miles per hour faster than the trolley. If the bus travels \(9\) miles in the same amount of time the trolley can travel \(7\) miles, what is the average speed of each?
• Terry decided to jog the \(5\) miles to town. On the return trip, she walked the \(5\) miles home at half of the speed that she was able to jog. If the total trip took \(3\) hours, what was her average jogging speed?
• James drove the \(24\) miles to town and back in \(1\) hour. On the return trip, he was able to average \(20\) miles per hour faster than he averaged on the trip to town. What was his average speed on the trip to town?
• A light aircraft was able to travel \(189\) miles with a \(14\) mile per hour tailwind in the same time it was able to travel \(147\) miles against it. What was the speed of the aircraft in calm air?
• A jet flew \(875\) miles with a \(30\) mile per hour tailwind. On the return trip, against a \(30\) mile per hour headwind, it was able to cover only \(725\) miles in the same amount of time. How fast was the jet in calm air?
• A helicopter averaged \(90\) miles per hour in calm air. Flying with the wind it was able to travel \(250\) miles in the same amount of time it took to travel \(200\) miles against it. What is the speed of the wind?
• Mary and Joe took a road-trip on separate motorcycles. Mary’s average speed was \(12\) miles per hour less than Joe’s average speed. If Mary drove \(115\) miles in the same time it took Joe to drive \(145\) miles, what was Mary’s average speed?
• A boat averaged \(12\) miles per hour in still water. On a trip downstream, with the current, the boat was able to travel \(26\) miles. The boat then turned around and returned upstream \(33\) miles. How fast was the current if the total trip took \(5\) hours?
• If the river current flows at an average \(3\) miles per hour, a tour boat can make an \(18\)-mile tour downstream with the current and back the \(18\) miles against the current in \(4 \frac{1}{2}\) hours. What is the average speed of the boat in still water?
• Jose drove \(10\) miles to his grandmother’s house for dinner and back that same evening. Because of traffic, he averaged \(20\) miles per hour less on the return trip. If it took \(\frac{1}{4}\) hour longer to get home, what was his average speed driving to his grandmother’s house?
• Jerry paddled his kayak, upstream against a \(1\) mph current, for \(12\) miles. The return trip, downstream with the \(1\) mph current, took one hour less time. How fast did Jerry paddle the kayak in still water?
• James and Mildred left the same location in separate cars and met in Los Angeles \(300\) miles away. James was able to average \(10\) miles an hour faster than Mildred on the trip. If James arrived \(1\) hour earlier than Mildred, what was Mildred’s average speed?
• A bus is \(20\) miles per hour faster than a bicycle. If Bill boards a bus at the same time and place that Mary departs on her bicycle, Bill will arrive downtown \(5\) miles away \(\frac{1}{3}\) hour earlier than Mary. What is the average speed of the bus?

1. \(20\) miles per hour

3. \(240\) miles per hour

5. \(52\) miles per hour

7. \(5\) miles per hour

9. \(112\) miles per hour

11. \(10\) miles per hour

13. \(1\) mile per hour

15. \(40\) miles per hour

17. \(50\) miles per hour

Exercise \(\PageIndex{5}\)

• Mike can paint the office by himself in \(4 \frac{1}{2}\) hours. Jordan can paint the office in \(6\) hours. How long will it take them to paint the office working together?
• Barry can lay a brick driveway by himself in \(3 \frac{1}{2}\) days. Robert does the same job in \(5\) days. How long will it take them to lay the brick driveway working together?
• A larger pipe fills a water tank twice as fast as a smaller pipe. When both pipes are used, they fill the tank in \(10\) hours. If the larger pipe is left off, how long would it take the smaller pipe to fill the tank?
• A newer printer can print twice as fast as an older printer. If both printers working together can print a batch of flyers in \(45\) minutes, then how long would it take the older printer to print the batch working alone?
• Mary can assemble a bicycle for display in \(2\) hours. It takes Jane \(3\) hours to assemble a bicycle. How long will it take Mary and Jane, working together, to assemble \(5\) bicycles?
• Working alone, James takes twice as long to assemble a computer as it takes Bill. In one \(8\)-hour shift, working together, James and Bill can assemble \(6\) computers. How long would it take James to assemble a computer if he were working alone?
• Working alone, it takes Harry one hour longer than Mike to install a fountain. Together they can install \(10\) fountains in \(12\) hours. How long would it take Mike to install \(10\) fountains by himself?
• Working alone, it takes Henry \(2\) hours longer than Bill to paint a room. Working together they painted \(2 \frac{1}{2}\) rooms in \(6\) hours. How long would it have taken Henry to paint the same amount if he were working alone?
• Manny, working alone, can install a custom cabinet in \(3\) hours less time than his assistant. Working together they can install the cabinet in \(2\) hours. How long would it take Manny to install the cabinet working alone?
• Working alone, Garret can assemble a garden shed in \(5\) hours less time than his brother. Working together, they need \(6\) hours to build the garden shed. How long would it take Garret to build the shed working alone?
• Working alone, the assistant-manager takes \(2\) more hours than the manager to record the inventory of the entire shop. After working together for \(2\) hours, it took the assistant-manager \(1\) additional hour to complete the inventory. How long would it have taken the manager to complete the inventory working alone?
• An older printer can print a batch of sales brochures in \(16\) minutes. A newer printer can print the same batch in \(10\) minutes. After working together for some time, the newer printer was shut down and it took the older printer \(3\) more minutes to complete the job. How long was the newer printer operating?

1. \(2 \frac{4}{7}\) hours

3. \(30\) hours

5. \(6\) hours

7. \(20\) hours

9. \(3\) hours

11. \(4\) hours

Exercise \(\PageIndex{6}\)

Translate each of the following sentences into a mathematical formula.

• The distance \(D\) an automobile can travel is directly proportional to the time \(t\) that it travels at a constant speed.
• The extension of a hanging spring \(d\) is directly proportional to the weight \(w\) attached to it.
• An automobile’s braking distance \(d\) is directly proportional to the square of the automobile’s speed \(v\).
• The volume \(V\) of a sphere varies directly as the cube of its radius \(r\).
• The volume \(V\) of a given mass of gas is inversely proportional to the pressure \(p\) exerted on it.
• Every particle of matter in the universe attracts every other particle with a force \(F\) that is directly proportional to the product of the masses \(m_{1}\) and \(m_{2}\) of the particles, and it is inversely proportional to the square of the distance d between them.
• Simple interest \(I\) is jointly proportional to the annual interest rate \(r\) and the time \(t\) in years a fixed amount of money is invested.
• The time \(t\) it takes an object to fall is directly proportional to the square root of the distance \(d\) it falls.

1. \(D=kt\)

3. \(d=kv^{2}\)

5. \(V = \frac{k}{p}\)

7. \(I=krt\)

Exercise \(\PageIndex{7}\)

Construct a mathematical model given the following:

• \(y\) varies directly as \(x\), and \(y=30\) when \(x=6\).
• \(y\) varies directly as \(x\), and \(y=52\) when \(x=4\).
• \(y\) is directly proportional to \(x\), and \(y=12\) when \(x=3\).
• \(y\) is directly proportional to \(x\), and \(y=120\) when \(x=20\).
• \(y\) is directly proportional to \(x\), and \(y=3\) when \(x=9\).
• \(y\) is directly proportional to \(x\), and \(y=21\) when \(x=3\).
• \(y\) varies inversely as \(x\), and \(y=2\) when \(x=\frac{1}{8}\).
• \(y\) varies inversely as \(x\), and \(y=\frac{3}{2}\) when \(x=\frac{1}{9}\).
• \(y\) is jointly proportional to \(x\) and \(z\), where \(y=2\) when \(x=1\) and \(z=3\).
• \(y\) is jointly proportional to \(x\) and \(z\), where \(y=15\) when \(x=3\) and \(z=7\).
• \(y\) varies jointly as \(x\) and \(z\), where \(y=\frac{2}{3}\) when \(x=\frac{1}{2}\) and \(z=12\).
• \(y\) varies jointly as \(x\) and \(z\), where \(y=5\) when \(x=\frac{3}{2}\) and \(z=\frac{2}{9}\).
• \(y\) varies directly as the square of \(x\), where \(y=45\) when \(x=3\).
• \(y\) varies directly as the square of \(x\), where \(y=3\) when \(x=\frac{1}{2}\).
• \(y\) is inversely proportional to the square of \(x\), where \(y=27\) when \(x=\frac{1}{3}\).
• \(y\) is inversely proportional to the square of \(x\), where \(y=9\) when \(x=\frac{2}{3}\).
• \(y\) varies jointly as \(x\) and the square of \(z\), where \(y=6\) when \(x=\frac{1}{4}\) and \(z=\frac{2}{3}\).
• \(y\) varies jointly as \(x\) and \(z\) and inversely as the square of \(w\), where \(y=5\) when \(z=1, z=3\), and \(w=\frac{1}{2}\).
• \(y\) varies directly as the square root of \(x\) and inversely as the square of \(z\), where \(y=15\) when \(x=25\) and \(z=2\).
• \(y\) varies directly as the square of \(x\) and inversely as \(z\) and the square of \(w\), where \(y=14\) when \(x=4, w=2\) and \(z=2\).

1. \(y=5x\)

3. \(y=4x\)

5. \(y=\frac{27}{x}\)

7. \(y=\frac{1}{4x}\)

9. \(y=\frac{2}{3}xz\)

11. \(y=\frac{1}{9}xz\)

13. \(y=5x^{2}\)

15. \(y = \frac { 3 } { x ^ { 2 } }\)

17. \(y = 54 x z ^ { 2 }\)

19. \(y = \frac { 12 \sqrt { x } } { z ^ { 2 } }\)

Exercise \(\PageIndex{8}\)

Solve applications involving variation.

• Revenue in dollars is directly proportional to the number of branded sweatshirts sold. The revenue earned from selling \(25\) sweatshirts is \($318.75\). Determine the revenue if \(30\) sweatshirts are sold.
• The sales tax on the purchase of a new car varies directly as the price of the car. If an \($18,000\) new car is purchased, then the sales tax is \($1,350\). How much sales tax is charged if the new car is priced at \($22,000\)?
• The price of a share of common stock in a company is directly proportional to the earnings per share (EPS) of the previous \(12\) months. If the price of a share of common stock in a company is $22.55, and the EPS is published to be \($1.10\), determine the value of the stock if the EPS increases by \($0.20\).
• The distance traveled on a road trip varies directly with the time spent on the road. If a \(126\)-mile trip can be made in \(3\) hours, then what distance can be traveled in \(4\) hours?
• The circumference of a circle is directly proportional to its radius. The circumference of a circle with radius \(7\) centimeters is measured as \(14π\) centimeters. What is the constant of proportionality?
• The area of circle varies directly as the square of its radius. The area of a circle with radius \(7\) centimeters is determined to be \(49π\) square centimeters. What is the constant of proportionality?
• The surface area of a sphere varies directly as the square of its radius. When the radius of a sphere measures \(2\) meters, the surface area measures \(16π\) square meters. Find the surface area of a sphere with radius \(3\) meters.
• The volume of a sphere varies directly as the cube of its radius. When the radius of a sphere measures \(3\) meters, the volume is \(36π\) cubic meters. Find the volume of a sphere with radius \(1\) meter.
• With a fixed height, the volume of a cone is directly proportional to the square of the radius at the base. When the radius at the base measures \(10\) centimeters, the volume is \(200\) cubic centimeters. Determine the volume of the cone if the radius of the base is halved.
• The distance \(d\) an object in free fall drops varies directly with the square of the time \(t\) that it has been falling. If an object in free fall drops \(36\) feet in \(1.5\) seconds, then how far will it have fallen in \(3\) seconds?

1. \($382.50\)

3. \($26.65\)

5. \(2π\)

7. \(36π\) square meters

9. \(50\) cubic centimeters

Exercise \(\PageIndex{9}\)

Hooke’s law suggests that the extension of a hanging spring is directly proportional to the weight attached to it. The constant of variation is called the spring constant.

• A hanging spring is stretched \(5\) inches when a \(20\)-pound weight is attached to it. Determine its spring constant.
• A hanging spring is stretched \(3\) centimeters when a \(2\)-kilogram weight is attached to it. Determine the spring constant.
• If a hanging spring is stretched \(3\) inches when a \(2\)-pound weight is attached, how far will it stretch with a \(5\)-pound weight attached?
• If a hanging spring is stretched \(6\) centimeters when a \(4\)-kilogram weight is attached to it, how far will it stretch with a \(2\)-kilogram weight attached?

1. \(\frac{1}{4}\)

3. \(7.5\) inches

Exercise \(\PageIndex{10}\)

The braking distance of an automobile is directly proportional to the square of its speed.

• It takes \(36\) feet to stop a particular automobile moving at a speed of \(30\) miles per hour. How much breaking distance is required if the speed is \(35\) miles per hour?
• After an accident, it was determined that it took a driver \(80\) feet to stop his car. In an experiment under similar conditions, it takes \(45\) feet to stop the car moving at a speed of \(30\) miles per hour. Estimate how fast the driver was moving before the accident.

1. \(49\) feet

Exercise \(\PageIndex{11}\)

Boyle’s law states that if the temperature remains constant, the volume \(V\) of a given mass of gas is inversely proportional to the pressure \(p\) exerted on it.

• A balloon is filled to a volume of \(216\) cubic inches on a diving boat under \(1\) atmosphere of pressure. If the balloon is taken underwater approximately \(33\) feet, where the pressure measures \(2\) atmospheres, then what is the volume of the balloon?
• A balloon is filled to \(216\) cubic inches under a pressure of \(3\) atmospheres at a depth of \(66\) feet. What would the volume be at the surface, where the pressure is \(1\) atmosphere?
• To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a \(72\)-pound boy is sitting \(3\) feet from the fulcrum, how far from the fulcrum must a \(54\)-pound boy sit to balance the seesaw?
• The current \(I\) in an electrical conductor is inversely proportional to its resistance \(R\). If the current is \(\frac{1}{4}\) ampere when the resistance is \(100\) ohms, what is the current when the resistance is \(150\) ohms?
• The amount of illumination \(I\) is inversely proportional to the square of the distance \(d\) from a light source. If \(70\) foot-candles of illumination is measured \(2\) feet away from a lamp, what level of illumination might we expect \(\frac{1}{2}\) foot away from the lamp?
• The amount of illumination \(I\) is inversely proportional to the square of the distance \(d\) from a light source. If \(40\) foot-candles of illumination is measured \(3\) feet away from a lamp, at what distance can we expect \(10\) foot-candles of illumination?
• The number of men, represented by \(y\), needed to lay a cobblestone driveway is directly proportional to the area \(A\) of the driveway and inversely proportional to the amount of time \(t\) allowed to complete the job. Typically, \(3\) men can lay \(1,200\) square feet of cobblestone in \(4\) hours. How many men will be required to lay \(2,400\) square feet of cobblestone in \(6\) hours?
• The volume of a right circular cylinder varies jointly as the square of its radius and its height. A right circular cylinder with a \(3\)-centimeter radius and a height of \(4\) centimeters has a volume of \(36π\) cubic centimeters. Find a formula for the volume of a right circular cylinder in terms of its radius and height.
• The period \(T\) of a pendulum is directly proportional to the square root of its length \(L\). If the length of a pendulum is \(1\) meter, then the period is approximately \(2\) seconds. Approximate the period of a pendulum that is \(0.5\) meter in length.
• The time \(t\) it takes an object to fall is directly proportional to the square root of the distance \(d\) it falls. An object dropped from \(4\) feet will take \(\frac{1}{2}\) second to hit the ground. How long will it take an object dropped from \(16\) feet to hit the ground?

1. \(108\) cubic inches

3. \(4\) feet

5. \(1,120\) foot-candles

7. \(4\) men

9. \(1.4\) seconds

Exercise \(\PageIndex{12}\)

Newton’s universal law of gravitation states that every particle of matter in the universe attracts every other particle with a force \(F\) that is directly proportional to the product of the masses \(m_{1}\) and \(m_{2}\) of the particles and inversely proportional to the square of the distance \(d\) between them. The constant of proportionality is called the gravitational constant.

• If two objects with masses \(50\) kilograms and \(100\) kilograms are \(\frac{1}{2}\) meter apart, then they produce approximately \(1.34 × 10^{−6}\) newtons (N) of force. Calculate the gravitational constant.
• Use the gravitational constant from the previous exercise to write a formula that approximates the force \(F\) in newtons between two masses \(m_{1}\) and \(m_{2}\), expressed in kilograms, given the distance \(d\) between them in meters.
• Calculate the force in newtons between Earth and the Moon, given that the mass of the Moon is approximately \(7.3 × 10^{22}\) kilograms, the mass of Earth is approximately \(6.0 × 10^{24}\) kilograms, and the distance between them is on average \(1.5 × 10^{11}\) meters.
• Calculate the force in newtons between Earth and the Sun, given that the mass of the Sun is approximately \(2.0 × 10^{30}\) kilograms, the mass of Earth is approximately \(6.0 × 10^{24}\) kilograms, and the distance between them is on average \(3.85 × 10^{8}\) meters.
• If \(y\) varies directly as the square of \(x\), then how does \(y\) change if \(x\) is doubled?
• If \(y\) varies inversely as square of \(t\), then how does \(y\) change if \(t\) is doubled?
• If \(y\) varies directly as the square of \(x\) and inversely as the square of \(t\), then how does \(y\) change if both \(x\) and \(t\) are doubled?

1. \(6.7 \times 10 ^ { - 11 } \mathrm { Nm } ^ { 2 } / \mathrm { kg } ^ { 2 }\)

3. \(1.98 \times 10 ^ { 20 } \mathrm { N }\)

5. \(y\) changes by a factor of \(4\)

7. \(y\) remains unchanged

37 Described by the formula \(D = rt\), where the distance \(D\) is given as the product of the average rate \(r\) and the time \(t\) traveled at that rate.

38 The rate at which a task can be performed.

39 \(\frac { 1 } { t _ { 1 } } \cdot t + \frac { 1 } { t _ { 2 } } \cdot t = 1\), where \(\frac { 1 } { t _ { 1 } }\) and \(\frac { 1 } { t _ { 2 } }\) are the individual work rates and t is the time it takes to complete the task working together.

40 Describes two quantities \(x\) and \(y\) that are constant multiples of each other: \(y = kx\).

41 The nonzero multiple \(k\), when quantities vary directly or inversely.

42 Used when referring to the constant of variation.

43 Used when referring to direct variation.

44 Describes two quantities \(x\) and \(y\), where one variable is directly proportional to the reciprocal of the other: \(y = \frac{k}{x}\).

45 Used when referring to inverse variation.

46 Describes a quantity \(y\) that varies directly as the product of two other quantities \(x\) and \(z: y = kxz\).

47 Used when referring to joint variation.

Chapter 4 Dynamics: Force and Newton’s Laws of Motion

4.6 Problem-Solving Strategies

• Understand and apply a problem-solving procedure to solve problems using Newton’s laws of motion.

Success in problem solving is obviously necessary to understand and apply physical principles, not to mention the more immediate need of passing exams. The basics of problem solving, presented earlier in this text, are followed here, but specific strategies useful in applying Newton’s laws of motion are emphasized. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, and so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy for Newton’s Laws of Motion

Step 1. As usual, it is first necessary to identify the physical principles involved. Once it is determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation . Such a sketch is shown in Figure 1 (a). Then, as in Figure 1 (b), use arrows to represent all forces, label them carefully, and make their lengths and directions correspond to the forces they represent (whenever sufficient information exists).

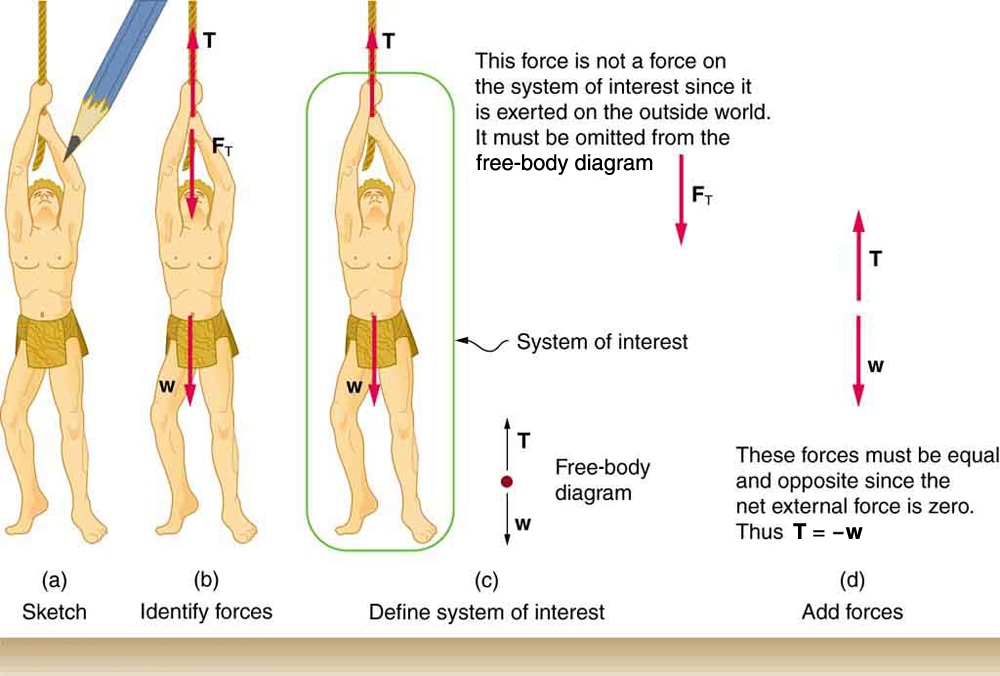
Step 2. Identify what needs to be determined and what is known or can be inferred from the problem as stated. That is, make a list of knowns and unknowns. Then carefully determine the system of interest . This decision is a crucial step, since Newton’s second law involves only external forces. Once the system of interest has been identified, it becomes possible to determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure 1 (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated earlier in this chapter, the system of interest depends on what question we need to answer. This choice becomes easier with practice, eventually developing into an almost unconscious process. Skill in clearly defining systems will be beneficial in later chapters as well.

A diagram showing the system of interest and all of the external forces is called a free-body diagram . Only forces are shown on free-body diagrams, not acceleration or velocity. We have drawn several of these in worked examples. Figure 1 (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Step 3. Once a free-body diagram is drawn, Newton’s second law can be applied to solve the problem . This is done in Figure 1 (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then they add like scalars. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. This is done by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known.

Applying Newton’s Second Law

Before you write net force equations, it is critical to determine whether the system is accelerating in a particular direction. If the acceleration is zero in a particular direction, then the net force is zero in that direction. Similarly, if the acceleration is nonzero in a particular direction, then the net force is described by the equation: [latex]{F_{\text{net}}=ma}.[/latex]

For example, if the system is accelerating in the horizontal direction, but it is not accelerating in the vertical direction, then you will have the following conclusions:

You will need this information in order to determine unknown forces acting in a system.

Step 4. As always, check the solution to see whether it is reasonable . In some cases, this is obvious. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving, and with experience it becomes progressively easier to judge whether an answer is reasonable. Another way to check your solution is to check the units. If you are solving for force and end up with units of m/s, then you have made a mistake.

Section Summary

• Draw a sketch of the problem.
• Identify known and unknown quantities, and identify the system of interest. Draw a free-body diagram, which is a sketch showing all of the forces acting on an object. The object is represented by a dot, and the forces are represented by vectors extending in different directions from the dot. If vectors act in directions that are not horizontal or vertical, resolve the vectors into horizontal and vertical components and draw them on the free-body diagram.
• Write Newton’s second law in the horizontal and vertical directions and add the forces acting on the object. If the object does not accelerate in a particular direction (for example, the [latex]{x}[/latex] -direction) then [latex]{F_{\text{net} \; x}=0}.[/latex] If the object does accelerate in that direction, [latex]{F_{\text{net} \; x}=ma}.[/latex]
• Check your answer. Is the answer reasonable? Are the units correct?

Problems & Exercises

1: A [latex]{5.00\times10^5\text{-kg}}[/latex] rocket is accelerating straight up. Its engines produce [latex]{1.250\times10^7\text{ N}}[/latex] of thrust, and air resistance is [latex]{4.50\times10^6\text{ N}}.[/latex] What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

2: The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is [latex]{1.80\text{ m/s}^2},[/latex] what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.

3: Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

4: When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

5: A freight train consists of two [latex]{8.00\times10^4\text{-kg}}[/latex] engines and 45 cars with average masses of [latex]{5.50\times10^4\text{ kg}}.[/latex] (a) What force must each engine exert backward on the track to accelerate the train at a rate of [latex]{5.00\times10^{-2}\text{ m/s}^2}[/latex] if the force of friction is [latex]{7.50\times10^5\text{ N}},[/latex] assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?

6: Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of [latex]{1.75\times10^4\text{ N}}[/latex] backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is [latex]{0.150\text{ m/s}^2},[/latex] what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.

7: A 1100-kg car pulls a boat on a trailer. (a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of [latex]{0.550\text{ m/s}^2}?[/latex] The mass of the boat plus trailer is 700 kg. (b) What is the force in the hitch between the car and the trailer if 80% of the resisting forces are experienced by the boat and trailer?

8: (a) Find the magnitudes of the forces [latex]{\textbf{F}_1}[/latex] and [latex]{\textbf{F}_2}[/latex] that add to give the total force [latex]{\textbf{F}_{\text{tot}}}[/latex] shown in Figure 2 . This may be done either graphically or by using trigonometry. (b) Show graphically that the same total force is obtained independent of the order of addition of [latex]{\textbf{F}_1}[/latex] and [latex]{\textbf{F}_2}.[/latex] (c) Find the direction and magnitude of some other pair of vectors that add to give [latex]{\textbf{F}_{\text{tot}}}.[/latex] Draw these to scale on the same drawing used in part (b) or a similar picture.

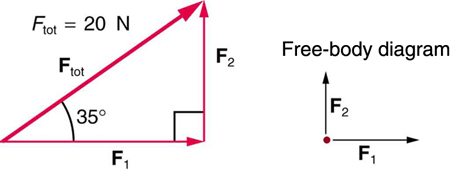
9: Two children pull a third child on a snow saucer sled exerting forces [latex]{\textbf{F}_1}[/latex] and [latex]{\textbf{F}_2}[/latex] as shown from above in Figure 3 . Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of [latex]{\textbf{F}_1}[/latex] and [latex]{\textbf{F}_2}.[/latex]

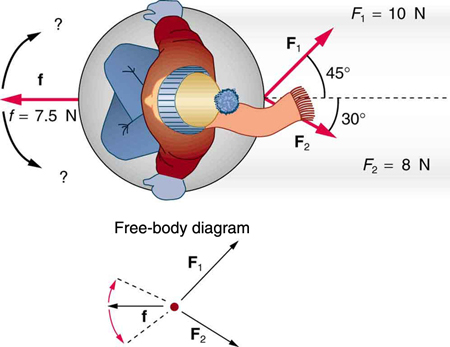
10: Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure 4 to pull it out. (a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is 2.00°? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. (b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to 7.00° and you still apply the force found in part (a) to its center?

11: What force is exerted on the tooth in Figure 5 if the tension in the wire is 25.0 N? Note that the force applied to the tooth is smaller than the tension in the wire, but this is necessitated by practical considerations of how force can be applied in the mouth. Explicitly show how you follow steps in the Problem-Solving Strategy for Newton’s laws of motion.

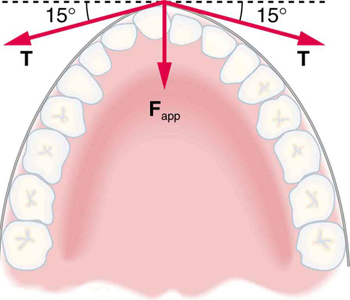
12: Figure 6 shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible. (a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope. (b) Find the tension in the rope above Superhero. (c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.

13: A nurse pushes a cart by exerting a force on the handle at a downward angle [latex]{35.0^{\circ}}[/latex] below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N. (a) Draw a free-body diagram for the system of interest. (b) What force must the nurse exert to move at a constant velocity?

14: Construct Your Own Problem Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.

15: Construct Your Own Problem Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children.

16: Unreasonable Results (a) Repeat Exercise 7 , but assume an acceleration of [latex]{1.20\text{ m/s}^2}[/latex] is produced. (b) What is unreasonable about the result? (c) Which premise is unreasonable, and why is it unreasonable?

17: Unreasonable Results (a) What is the initial acceleration of a rocket that has a mass of [latex]{1.50\times10^6\text{ kg}}[/latex] at takeoff, the engines of which produce a thrust of [latex]{2.00\times10^6\text{ N}}?[/latex] Do not neglect gravity. (b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.) (c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)

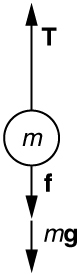
Using the free-body diagram:

[latex]{F_{\text{net}}=T-f-mg=ma},[/latex]

[latex]{ a = \frac{T - f - mg}{m} = \frac{1.250 \times 10^7 \; \textbf{N} - 4.50 \times 10^6 \; N - (5.00 \times 10^5 \;\text{kg})(9.80 \;\text{m/s}^2)}{5.00 \times 10^5 \;\text{kg}} = 6.20 \;\text{m/s}^2}[/latex]

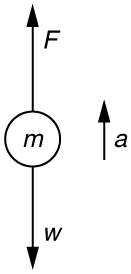
• Use Newton’s laws of motion

Find: [latex]{F}.[/latex]

[latex]{F=(70.0\text{ kg})[(39.2\text{ m/s}^2)+(9.80\text{ m/s}^2)]=3.43\times10^3\text{ N}}.[/latex] The force exerted by the high-jumper is actually down on the ground, but [latex]{F}[/latex] is up from the ground and makes him jump.

• This result is reasonable, since it is quite possible for a person to exert a force of the magnitude of [latex]{10^3\text{ N}}.[/latex]

(a) [latex]{4.41\times10^5\text{ N}}[/latex]

(b) [latex]{1.50\times10^5\text{ N}}[/latex]

(a) [latex]{910\text{ N}}[/latex]

(b) [latex]{1.11\times10^3\text{ N}}[/latex]

[latex]{a=0.139\text{ m/s}},{\theta=12.4^{\circ}}[/latex] north of east

• Use Newton’s laws since we are looking for forces.

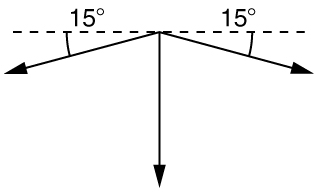
The x -components of the tension cancel. [latex]{\sum{F}_x=0}.[/latex]

• This seems reasonable, since the applied tensions should be greater than the force applied to the tooth.

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• TPC and eLearning
• Read Watch Interact
• What's NEW at TPC?
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Horizontally Launched Projectile Problems
• What is a Projectile?
• Motion Characteristics of a Projectile
• Horizontal and Vertical Velocity
• Horizontal and Vertical Displacement
• Initial Velocity Components
• Non-Horizontally Launched Projectile Problems

There are two basic types of projectile problems that we will discuss in this course. While the general principles are the same for each type of problem, the approach will vary due to the fact the problems differ in terms of their initial conditions. The two types of problems are:

A projectile is launched with an initial horizontal velocity from an elevated position and follows a parabolic path to the ground. Predictable unknowns include the initial speed of the projectile, the initial height of the projectile, the time of flight, and the horizontal distance of the projectile.

Examples of this type of problem are

• A pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

A projectile is launched at an angle to the horizontal and rises upwards to a peak while moving horizontally. Upon reaching the peak, the projectile falls with a motion that is symmetrical to its path upwards to the peak. Predictable unknowns include the time of flight, the horizontal range, and the height of the projectile when it is at its peak.

• A football is kicked with an initial velocity of 25 m/s at an angle of 45-degrees with the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the football.
• A long jumper leaves the ground with an initial velocity of 12 m/s at an angle of 28-degrees above the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the long-jumper.

The second problem type will be the subject of the next part of Lesson 2 . In this part of Lesson 2, we will focus on the first type of problem - sometimes referred to as horizontally launched projectile problems. Three common kinematic equations that will be used for both type of problems include the following:

d = v i •t + 0.5*a*t 2 v f = v i + a•t v f 2  = v i 2  + 2*a•d  

Equations for the Horizontal Motion of a Projectile

The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions - both horizontally and vertically. Since these two components of motion are independent of each other, two distinctly separate sets of equations are needed - one for the projectile's horizontal motion and one for its vertical motion. Thus, the three equations above are transformed into two sets of three equations. For the horizontal components of motion, the equations are

x = v i x •t + 0.5*a x *t 2

v f x  = v i x  + a x •t

v f x 2  = v i x 2  + 2*a x •x

Of these three equations, the top equation is the most commonly used. An application of projectile concepts to each of these equations would also lead one to conclude that any term with a x in it would cancel out of the equation since a x = 0 m/s/s . Once this cancellation of ax terms is performed, the only equation of usefulness is:

x = v i x •t

Equations for the Vertical Motion of a Projectile

For the vertical components of motion, the three equations are

y = v iy •t + 0.5*a y *t 2

v fy  = v iy  + a y •t

v fy 2  = v iy 2  + 2*a y •y

In each of the above equations, the vertical acceleration of a projectile is known to be -9.8 m/s/s (the acceleration of gravity). Furthermore, for the special case of the first type of problem (horizontally launched projectile problems), v iy = 0 m/s. Thus, any term with v iy in it will cancel out of the equation.

The two sets of three equations above are the kinematic equations that will be used to solve projectile motion problems.

Solving Projectile Problems

To illustrate the usefulness of the above equations in making predictions about the motion of a projectile, consider the solution to the following problem.

The solution of this problem begins by equating the known or given values with the symbols of the kinematic equations - x, y, v ix , v iy , a x , a y , and t. Because horizontal and vertical information is used separately, it is a wise idea to organized the given information in two columns - one column for horizontal information and one column for vertical information. In this case, the following information is either given or implied in the problem statement:

As indicated in the table, the unknown quantity is the horizontal displacement (and the time of flight) of the pool ball. The solution of the problem now requires the selection of an appropriate strategy for using the kinematic equations and the known information to solve for the unknown quantities. It will almost always be the case that such a strategy demands that one of the vertical equations be used to determine the time of flight of the projectile and then one of the horizontal equations be used to find the other unknown quantities (or vice versa - first use the horizontal and then the vertical equation). An organized listing of known quantities (as in the table above) provides cues for the selection of the strategy. For example, the table above reveals that there are three quantities known about the vertical motion of the pool ball. Since each equation has four variables in it, knowledge of three of the variables allows one to calculate a fourth variable. Thus, it would be reasonable that a vertical equation is used with the vertical values to determine time and then the horizontal equations be used to determine the horizontal displacement (x). The first vertical equation (y = v iy •t +0.5•a y •t 2 ) will allow for the determination of the time. Once the appropriate equation has been selected, the physics problem becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

Since the first term on the right side of the equation reduces to 0, the equation can be simplified to

If both sides of the equation are divided by -5.0 m/s/s, the equation becomes

By taking the square root of both sides of the equation, the time of flight can then be determined .

Once the time has been determined, a horizontal equation can be used to determine the horizontal displacement of the pool ball. Recall from the given information , v ix = 2.4 m/s and a x = 0 m/s/s. The first horizontal equation (x = v ix •t + 0.5•a x •t 2 ) can then be used to solve for "x." With the equation selected, the physics problem once more becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

Since the second term on the right side of the equation reduces to 0, the equation can then be simplified to

The answer to the stated problem is that the pool ball is in the air for 0.35 seconds and lands a horizontal distance of 0.84 m from the edge of the pool table.

The following procedure summarizes the above problem-solving approach.

• Carefully read the problem and list known and unknown information in terms of the symbols of the kinematic equations. For convenience sake, make a table with horizontal information on one side and vertical information on the other side.
• Identify the unknown quantity that the problem requests you to solve for.
• Select either a horizontal or vertical equation to solve for the time of flight of the projectile.
• With the time determined, use one of the other equations to solve for the unknown. (Usually, if a horizontal equation is used to solve for time, then a vertical equation can be used to solve for the final unknown quantity.)

One caution is in order. The sole reliance upon 4- and 5-step procedures to solve physics problems is always a dangerous approach. Physics problems are usually just that - problems! While problems can often be simplified by the use of short procedures as the one above, not all problems can be solved with the above procedure. While steps 1 and 2 above are critical to your success in solving horizontally launched projectile problems, there will always be a problem that doesn't fit the mold . Problem solving is not like cooking; it is not a mere matter of following a recipe. Rather, problem solving requires careful reading, a firm grasp of conceptual physics, critical thought and analysis, and lots of disciplined practice. Never divorce conceptual understanding and critical thinking from your approach to solving problems.

Check Your Understanding

Use y = v iy • t + 0.5 • a y • t 2 to solve for time; the time of flight is 2.12 seconds.

Now use x = v ix • t + 0.5 • a x • t 2 to solve for v ix

Note that a x is 0 m/s/s so the last term on the right side of the equation cancels. By substituting 35.0 m for x and 2.12 s for t, the v ix can be found to be 16.5 m/s.

We Would Like to Suggest ...

• Addition of Forces

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Mechanics (Essentials) - Class 11th

Course: mechanics (essentials) - class 11th   >   unit 5, how to solve a projectile motion problem.

• What is 2D projectile motion?
• Projectile at an angle
• Angled launch projectile vectors
• Comparing projectile trajectories
• Projectiles launched at an angle review
• Horizontally launched projectile
• Solving kinematic equations for horizontal projectiles
• Projectile motion graphs
• 2D projectile motion: Identifying graphs for projectiles
• 2D projectile motion: Vectors and comparing multiple trajectories

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Problem-Solving

• Last updated
• Save as PDF
• Page ID 16943

A General Approach

Basic problem-solving techniques can aid in the solution of problems involving motion (i.e., the laws of motion).

learning objectives

• Assess the laws of motion through practiced problem solving techniques

When dealing with the laws of motion, although knowledge of concepts and equations is important, understanding basic problem solving techniques can simplify the process of solving problems that may appear difficult. Your approach to problem solving can involve several key steps.

Free body diagram : An example of a drawing to help identify forces and directions.

First, gather all relevant information from the problem. Identify all quantities that are given (the knowns ), then do the same for all quantities needed (the unknowns ). Also, identify the physical principles involved (e.g., force, gravity, friction, etc. ).

Next, a drawing may be helpful. Sometimes a drawing can even help determine the known and unknown quantities. It need not be a work of art, but it should be clear enough to illustrate proper dimension, (meaning one, two, or three dimensions). You can then use this drawing to determine which direction is positive and which is negative (making note of this on the drawing).

A next step is to use what is known to find the appropriate equation to find what is unknown. While it is easiest to find an equation that leaves only one unknown, sometimes this is not possible. In these situations, you can solve multiple equations to find the right answer. Remember that equations represent physical principles and relationships, so use the equations and drawings in tandem.

You may then substitute the knowns into the appropriate equations and find a numerical solution.

Check the answer to see if it is reasonable and makes sense. Your judgment will improve and fine tune as you solve more problems of this nature. This “judgement” step helps intuit the problem in terms of its conceptual meaning. If you can judge whether the answer is reasonable, you have a deeper understanding of physics than simply the mechanics of problem solving.

When solving problems, we tend to perform these steps in different order, as well as do several steps simultaneously. There is no rigid procedure that will work every time. Creativity and insight grow with experience. In time, the basics of problem solving can become relatively automatic.

• Gathering all relevant information and identifying knowns and unknowns is an important first step.
• Always make a drawing to help identify directions of forces and to establish \(\mathrm{x, y}\), and \(\mathrm{z}\) axes.
• Choose the correct equations, solve the problem, and check that the answer fits expectations numerically.
• equation : An assertion that two expressions are equal, expressed by writing the two expressions separated by an equal sign; from which one is to determine a particular quantity.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• OpenStax College, College Physics. September 17, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42125/latest/?collection=col11406/latest . License : CC BY: Attribution
• equation. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/equation . License : CC BY-SA: Attribution-ShareAlike
• Free body diagram. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Free_body_diagram . License : Public Domain: No Known Copyright

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

24 Projectile Motion

So far we have only discussed objects in free fall that are going up and down.  However, objects in free fall can also have motion along the horizontal direction. This is often referred to as  projectile motion .  Let’s look at one such example.

Exercise 24.1: Kicking a Ball

Since this is our first problem in 2D problem involving forces, we will go through it step by step.

Now our picture.  I find it helpful to trace out the path of the ball, which we know goes up and down in an arc.  If you’re not sure how I got my picture, I also added a video in which I go through the whole process.

Now find relations. Since this is a problem involving motion in 2D,  we will need to write Newton’s laws for each object and for each axis!

Use the relations we just derived to determine how far the ball travels.

Use your to determine at what angle you should kick the ball to achieve the longest possible kick.  You could do this with calculus, but I think it is much more gratifying if you just reason it out in English.

I want to emphasize two things about our solution above:

• When solving force problems, we always need to write Newton’s law for each object, for each axis.
• Once we have our forces set, we can treat the two axis independently of each other .

Let’s do another projectile motion problem.

Exercise 24.2: Cannon Shot

Follow the 4 steps of problem solving.  You can peak at my solution if you get stuck, but then try to finish up the problem on your own.

To end, let’s try a more conceptual question (no math needed!).

Exercise 24.3: Bullet Fired vs Bullet Dropped

A bullet is fired from a gun that is pointed perfectly horizontally.  At the exact same time, a second bullet is dropped from the exact same height.

Fortunately for us, the Myth Busters performed this exact experiment.

This problem highlights a point we raised earlier: the kinematic equations for one axis are completely independent of what is happening in other axis .  The “dropping” motion of the bullet is along the y-axis, so whatever is going on along the x-axis (i.e. the bullet being fired) is completely irrelevant .

Key Takeaways

Introductory Physics: Classical Mechanics Copyright © by . All Rights Reserved.

Share This Book

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 20 March 2024
• Correction 21 March 2024

Mathematician who tamed randomness wins Abel Prize

• Davide Castelvecchi

You can also search for this author in PubMed   Google Scholar

Michel Talagrand studies stochastic processes, mathematical models of phenomena that are governed by randomness. Credit: Peter Bagde/Typos1/Abel Prize 2024

A mathematician who developed formulas to make random processes more predictable and helped to solve an iconic model of complex phenomena has won the 2024 Abel Prize, one of the field’s most coveted awards. Michel Talagrand received the prize for his “contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics”, the Norwegian Academy of Science and Letters in Oslo announced on 20 March.

Assaf Naor, a mathematician at Princeton University in New Jersey, says it is difficult to overestimate the impact of Talagrand’s work. “There are papers posted maybe on a daily basis where the punchline is ‘now we use Talagrand’s inequalities’,” he says.

Talagrand’s reaction on hearing the news was incredulity. “There was a total blank in my mind for at least four seconds,” he says. “If I had been told an alien ship had landed in front of the White House, I would not have been more surprised.”

The Abel Prize was modelled after the Nobel Prizes — which do not include mathematics — and was first awarded in 2003. The recipient wins a sum of 7.5 million Norwegian kroner (US$700,000).

‘Like a piece of art’

Talagrand specializes in the theory of probability and stochastic processes, which are mathematical models of phenomena governed by randomness. A typical example is a river’s water level, which is highly variable and is affected by many independent factors, including rain, wind and temperature, Talagrand says. His proudest achievement was his inequalities 1 , a set of formulas that poses limits to the swings in stochastic processes. His formulas express how the contributions of many factors often cancel each other out — making the overall result less variable, not more.

“It’s like a piece of art,” says Abel-committee chair Helge Holden, a mathematician at the Norwegian University of Science and Technology in Trondheim. “The magic here is to find a good estimate, not just a rough estimate.”

Abel Prize: pioneer of ‘smooth’ physics wins top maths award

Thanks to Talagrand’s techniques, “many things that seem complicated and random turn out to be not so random”, says Naor. His estimates are extremely powerful, for example for studying problems such as optimizing the route of a delivery truck. Finding a perfect solution would require an exorbitant amount of computation, so computer scientists can instead calculate the lengths of a limited number of random candidate routes and then take the average — and Talagrand’s inequalities ensure that the result is close to optimal.

Talagrand also completed the solution to a problem posed by theoretical physicist Giorgio Parisi — work that ultimately helped Parisi to earn a Nobel Prize in Physics in 2021. In 1979, Parisi, now at the University of Rome, proposed a complete solution for the structure of a spin glass — an abstracted model of a material in which the magnetization of each atom tends to flip up or down depending on those of its neighbours.

Parisi’s arguments were rooted in his powerful intuition in physics, and followed steps that “mathematicians would consider as sorcery”, Talagrand says, such as taking n copies of a system — with n being a negative number. Many researchers doubted that Parisi’s proof could be made mathematically rigorous. But in the early 2000s, the problem was completely solved in two separate works, one by Talagrand 2 and an earlier one by Francesco Guerra 3 , a mathematical physicist who is also at the University of Rome.

Finding motivation

Talagrand’s journey to becoming a top researcher was unconventional. Born in Béziers, France, in 1952, he lost vision in his right eye at age five because of a genetic predisposition to detachment of the retina. Although while growing up in Lyon he was a voracious reader of popular science magazines, he struggled at school, particularly with the complex rules of French spelling. “I never really made peace with orthography,” he told an interviewer in 2019 .

His turning point came at age 15, when he received emergency treatment for another retinal detachment, this time in his left eye. He had to miss almost an entire year of school. The terrifying experience of nearly losing his sight — and his father’s efforts to keep his mind busy while his eyes were bandaged — gave Talagrand a renewed focus. He became a highly motivated student after his recovery, and began to excel in national maths competitions.

Just 5 women have won a top maths prize in the past 90 years

Still, Talagrand did not follow the typical path of gifted French students, which includes two years of preparatory school followed by a national admission competition for highly selective grandes écoles such as the École Normale Supérieure in Paris. Instead, he studied at the University of Lyon, France, and then went on to work as a full-time researcher at the national research agency CNRS, first in Lyon and later in Paris, where he spent more than a decade in an entry-level job. Apart from a brief stint in Canada, followed by a trip to the United States where he met his wife, he worked at the CNRS until his retirement.

Talagrand loves to challenge other mathematicians to solve problems that he has come up with — offering cash to those who do — and he keeps a list of those problems on his website. Some have been solved, leading to publications in major maths journals . The prizes come with some conditions: “I will award the prizes below as long as I am not too senile to understand the proofs I receive. If I can’t understand them, I will not pay.”

doi: https://doi.org/10.1038/d41586-024-00839-6

Updates & Corrections

Correction 21 March 2024 : An earlier version of this article stated that Giorgio Parisi won the Nobel Prize in Physics in 2001. He in fact won in 2021.

Talagrand, M. Publ. Math. IHES 81 , 73–205, (1995).

Article   Google Scholar  

Talagrand, M. Ann. Math. 163 , 221–263 (2006).

Guerra, F. Commun. Math. Phys. 233 , 1–12 (2003).

Download references

Reprints and permissions

Related Articles

Fermat's last theorem earns Andrew Wiles the Abel Prize

'Beautiful mind' John Nash adds Abel Prize to his Nobel

• Mathematics and computing

Persistent interaction patterns across social media platforms and over time

Article 20 MAR 24

So … you’ve been hacked

Technology Feature 19 MAR 24

Three reasons why AI doesn’t model human language

Correspondence 19 MAR 24

Postdoctoral Associate- Cellular Neuroscience

Houston, Texas (US)

Baylor College of Medicine (BCM)

Postdoctoral Associate- Cancer Biology

Recruitment of talent positions at shengjing hospital of china medical university.

Call for top experts and scholars in the field of science and technology.

Shenyang, Liaoning, China

Shengjing Hospital of China Medical University

Assistant Professor in Plant Biology

The Plant Science Program in the Biological and Environmental Science and Engineering (BESE) Division at King Abdullah University of Science and Te...

Saudi Arabia (SA)

King Abdullah University of Science and Technology

Postdoctoral Associate

Our laboratory at the Washington University in St. Louis is seeking a postdoctoral experimental biologist to study urogenital diseases and cancer.

Saint Louis, Missouri

Washington University School of Medicine Department of Medicine

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies