distance formula problem solving

Distance Formula Questions

Distance formula questions with solutions are provided here for students to practice and understand how to find the distance between the two points in a Cartesian plane .

In coordinate geometry, the distance between two points A(x 1 , y 1 ) and B(x 2 , y 2 ) is given by

\(\begin{array}{l}AB = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\end{array} \)

This formula is used to find the distance between two points in a two-dimensional plane.

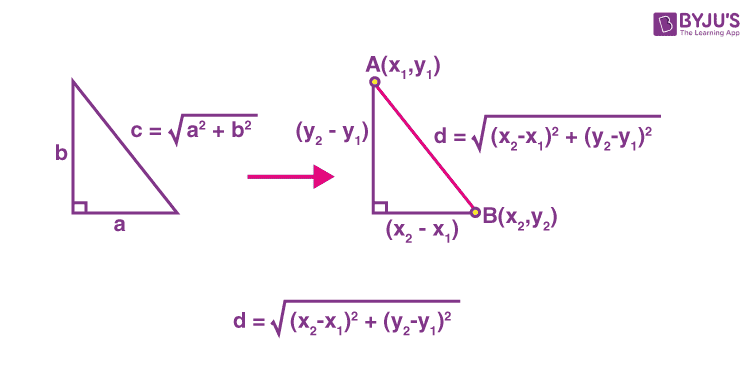
The distance between two points A(x 1 , y 2 , z 1 ) and B(x 2 , y 2 , z 2 ) in three dimensional plane is given by –

\(\begin{array}{l}AB = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}\end{array} \)

To see the derivation of the distance formula, click here .

Distance Formula Questions with Solutions

Let us apply the distance formula by solving some questions.

Question 1:

Find the distance between the following points:

(I) (-1, 2) and (2, 3)

(II) (0, 1) and (6, –1)

(III) (1, 0, –1) and (2, 0, 7)

(I) Let the distance between the points (-1, 2) and (2, 3) be d, then

d = √[(2 – ( –1)) 2 + (3 – 2) 2 ] = √[9 + 1] = √10 units.

(II) Let the distance between the points (0, 1) and (6, –1) be d, then

d = √[(6 – 0) 2 + ( –1 – 1) 2 ] = √[36 + 4] = √40 = 2√10 units.

(III) Let the distance between the points (1, 0, –1) and (2, 0, 7) be d, then

d = √[(2 – 1) 2 + (0 – 0) 2 + (7 – ( –1)) 2 ] = √[1 + 0 + 64] = √65 units.

Question 2:

Find a point on the x-axis which is equidistant from the points ( –5, 2) and (9, –2).

Let the points be P( –5, 2) and Q(9, –2) and let R(x , 0) be the point on x-axis which is equidistant from P and Q.

Now, PR = QR ⇒ PR 2 = QR 2

⇒ [(x – ( –5)) 2 + (0 – 2) 2 ] = [(x – 9) 2 + (0 – ( –2)) 2 ]

⇒ (x + 5) 2 + 4 = (x – 9) 2 + 4

⇒ x 2 + 10x + 25 = x 2 – 18x + 81

⇒ 10x + 18x = 81 – 25

⇒ x = 56/28 = 2

Therefore, the point is R(2, 0).

Question 3:

Show that the points P( –1, 6, 6), Q(0, 7, 10) and R( –4, 9, 6) form an isosceles right triangle.

Now, PQ = √[(0 +1) 2 + (7 – 6) 2 + (10 – 6) 2 ]

= √[1 + 1 + 16] = √18 = 3√2 units.

QR = √[( –4 – 0) 2 + (9 – 7) 2 + (6 – 10) 2 ]

= √[16 + 4 + 16] = √36 = 6 units.

PR = √[( –4 – ( –1)) 2 + (9 – 6) 2 + (6 – 6) 2 ]

= √[9 + 9 + 0] = √18 = 3√2 units.

Also, PQ 2 + PR 2 = QR 2 . Hence, PQR is a right isosceles triangle.

Question 4:

Show that the points A(2, 3), B(3, 4) and C(4, 5) are collinear.

Now, AB = √[(3 – 2) 2 + (4 – 3) 2 ]

= √[1 + 1] =√2 units

BC = √[(4 – 3) 2 + (5 – 4) 2 ]

= √[1 + 1] = √2 units

AC = √[(4 –2) 2 + (5 – 3) 2 ]

= √[2 2. + 2 2 ] = √8 = 2√2 units.

Clearly, AB + BC = AC

∴ the points are collinear.

Question 5:

The vertices of a triangle ABC are A(1, 2), B(3, –4), and C(5, –6). Find its circumcentre and circum-radius.

The circumcentre of a triangle is an interior point of a triangle equidistant from the vertices of the triangle, and the circum-radius is that equal distance.

Let O(x, y) be the circumcentre of the triangle ABC. the

AO = BO = CO ⇒ AO 2 = BO 2 = CO 2

AO 2 = BO 2

⇒ (x – 1) 2 + (y – 2) 2 = (x – 3) 2 + (y + 4) 2

⇒ x 2 – 2x + 1 + y 2 – 4y + 4 = x 2 – 6x + 9 + y 2 + 8y + 16

⇒ 4x – 12y = 25 – 5

⇒ x – 3y = 5 ….(i)

Again taking BO 2 = CO 2.

⇒ (x – 3) 2 + (y + 4) 2 = (x – 5) 2 + (y + 6) 2

⇒ –6x + 8y + 10x – 12y = 25 + 36 – 9 – 16

⇒ 4x – 4y = 36

⇒ x – y = 9 ….(ii)

Subtracting (ii) from (i) we get, y = 2 and x = 11

∴ the circumcentre is O(11, 2)

And the circum-radius is AO = √[(11 – 1) 2 + (2 – 2) 2 ] = 10 units.

• Centroid of a Triangle
• Orthocentre of a Triangle
• Section Formula

Question 6:

Find the area of the square whose one pair of opposite vertices are (3, 4) and (5, 6).

Let ABCD be the square and let A(3, 4) and C(5, 6) be the pair of opposite vertices of the square.

Now, AC makes the diagonal of the square and the area of a square is also given by (diagonal) 2 /2/

AC =√[(5 – 3) 2 + (6 – 4) 2 ] = √[2 2 + 2 2 ] = 2√2 units

Area of the square ABCD = AC 2 /2 = 8/2 = 4 square units.

Question 7:

Find the orthocentre of the triangle ABC such that A(2, 2), B(6, 3) and C(4, 11).

Let us find the length of each side of the triangle

AB = √[(6 – 2) 2 + (3 – 2) 2 ] = √[16 + 1] = √17 units.

BC = √[(4 – 6) 2 + (11 – 3) 2 ] = √4 + 64 = √68 units

AC = √[(4 – 2) 2 + (11 – 2) 2 ] = √[4 + 81] = √85 units

We see that AB 2 + BC 2 = AC 2

∴ triangle ABC is a right-angled triangle at B

Thus, the ortho-centre of the triangle ABC is at B(6, 3).

Question 8:

Find the center of the circle passing through points A(0, 5), B(3, 8), and C(6, 5).

Let O(x, y) be the center of the circle.

Then AO 2 = BO 2 = CO 2

Taking AO 2 = BO 2

⇒ (x – 0) 2 + (y – 5) 2 = (x – 3) 2 + (y – 8) 2

⇒ –10y + 6x + 16y = 9 + 64 – 25

⇒ 6x + 6y = 48

⇒ x + y = 8 ….(i)

Again taking BO 2 = CO 2

⇒ (x – 3) 2 + (y – 8) 2 = (x – 6) + (y – 5) 2

⇒ –6x –16y + 12x + 10y = 36 + 25 – 9 – 64

⇒ 6x – 6y = – 12

⇒ x – y = –2 ….(ii)

Adding (i) and (ii), we get

2x = 6 ⇒ x = 3 and y = 5

∴ O(3, 5) is the centre of the circle passing through points A(0, 5), B(3, 8) and C(6, 5).

Question 9:

If the point P(2, 1) lies on the line segment joining the points A(4, 2) and B(8, 4), then prove that AP = ½ AB.

Let us find the length of AP and AB,

AP = √[(2 – 4) 2 + (1 – 2) 2 ] = √[4 + 1] = √5 units.

AB = √[(8 – 4) 2 + (4 – 2) 2 ] = √[16 + 4] = 2√5 units.

Clearly, 2AP = AB

⇒ AP = ½ AB.

Question 10:

Find the coordinates of a point that is equidistant from the three vertices of a triangle (0, 0), (0, 2y), and (2x, 0).

Let the triangle be ABC such that A(0, 0), B(2x, 0), and C(0, 2y), and let P(h, k) be the point equidistant from all the points.

Then, PA 2 = PB 2 = PC 2

Taking, PA 2 = PB 2

⇒ (h – 0) 2 + (k – 0) 2 = (h – 2x) 2 + (k – 0) 2.

⇒ h 2 + k 2 = h 2 + 4x 2 – 4hx + k 2

⇒ 4hx = 4x 2.

Again taking, PB 2 = PC 2

⇒ (h – 2x) 2 + (k – 0) 2 = (h – 0) 2 + (k – 2y) 2

⇒ h 2 + 4x 2 – 4hx + k 2 = h 2 + k 2 – 4ky + 4y 2

⇒ 4x 2 – 4x 2 = –4ky + 4y 2 { ∵ h = x}

∴ the coordinates of the point are P(x, y).

Check your answers with the distance formula calculator .

<h2>Related Video Lesson</h2>

<div class=”youtube-video” data-video-thumbnail=””><img class=”tumbnailYT” src=” https://cdn1.byjus.com/wp-content/uploads/2020/01/section-formula-in-coordinate-geometry.jpg ” data-video=” https://www.youtube.com/embed/KowWdT5IcaQ ” /></div>

Practice Questions on Distance Formula

1. Find the distance between the following points:

(I) (2, 5) and (3, 6)

(II) ( –9, 3) and (3, 2)

(III) (4, 5, –2) and (0, –2, 3)

2. Find a point on the y-axis which is equidistant from the points ( –5, 2) and (9, –2).

3. Find the area of the square whose one pair of opposite vertices are (2, 6) and (6, 2).

4. Find the orthocentre of the triangle PQR such that P( –1, 6, 6), Q(0, 7, 10) and R( –4, 9, 6).

5. Find the coordinates of the fourth vertex of the parallelogram whose rest of the three vertices are ( –2, 3), (6, 7) and (8, 3).

Learn about various mathematical concepts in a simple manner with detailed information, along with step-by-step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalized videos.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Distance Problems with Solutions

The concept of the distance between two points is an important one in mathematics. A set of distance problems with detailed solutions (at the bottom of this page) are presented.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Distance and Midpoint Formulas and Circles

• Last updated
• Save as PDF
• Page ID 5188

Learning Objectives

By the end of this section, you will be able to:

Use the Distance Formula

Use the midpoint formula.

• Write the equation of a circle in standard form
• Graph a circle

Before you get started, take this readiness quiz.

• Find the length of the hypotenuse of a right triangle whose legs are \(12\) and \(16\) inches. If you missed this problem, review Example 2.34.
• Factor: \(x^{2}-18 x+81\). If you missed this problem, review Example 6.24.
• Solve by completing the square: \(x^{2}-12 x-12=0\). If you missed this problem, review Example 9.22.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,4)\) and \((2,1)\).

Exercise \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,1)\) and \((2,-2)\).

Exercise \(\PageIndex{2}\)

Use the rectangular coordinate system to find the distance between the points \((5,3)\) and \((-3,-3)\).

The method we used in the last example leads us to the formula to find the distance between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\).

When we found the length of the horizontal leg we subtracted \(6−2\) which is \(x_{2}-x_{1}\).

When we found the length of the vertical leg we subtracted \(4−1\) which is \(y_{2}-y_{1}\).

If the triangle had been in a different position, we may have subtracted \(x_{1}-x_{2}\) or \(y_{1}-y_{2}\). The expressions \(x_{2}-x_{1}\) and \(x_{1}-x_{2}\) vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\).

In the Pythagorean Theorem, we substitute the general expressions \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\) rather than the numbers.

\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)

This is the Distance Formula we use to find the distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\).

Definition \(\PageIndex{1}\)

Distance Formula

The distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\) is

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Example \(\PageIndex{2}\)

Use the Distance Formula to find the distance between the points \((-5,-3)\) and \((7,2)\).

Write the Distance Formula.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\), \(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) and substitute.

\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)

\(d=\sqrt{12^{2}+5^{2}}\) \(d=\sqrt{144+25}\) \(d=\sqrt{169}\) \(d=13\)

Exercise \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((-4,-5)\) and \((5,7)\).

Exercise \(\PageIndex{4}\)

Use the Distance Formula to find the distance between the points \((-2,-5)\) and \((-14,-10)\).

Example \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((10,−4)\) and \((−1,5)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\), \(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) and substitute.

\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)

\(d=\sqrt{(-11)^{2}+9^{2}}\) \(d=\sqrt{121+81}\) \(d=\sqrt{202}\)

Since \(202\) is not a perfect square, we can leave the answer in exact form or find a decimal approximation.

\(d=\sqrt{202}\) or \(d \approx 14.2\)

Exercise \(\PageIndex{5}\)

Use the Distance Formula to find the distance between the points \((−4,−5)\) and \((3,4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{130}, d \approx 11.4\)

Exercise \(\PageIndex{6}\)

Use the Distance Formula to find the distance between the points \((−2,−5)\) and \((−3,−4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{2}, d \approx 1.4\)

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Definition \(\PageIndex{2}\)

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is

\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Example \(\PageIndex{4}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−5,−4)\) and \((7,2)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Exercise \(\PageIndex{7}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−3,−5)\) and \((5,7)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Exercise \(\PageIndex{8}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−2,−5)\) and \((6,−1)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\). It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, is may be easier to remember the formulas.

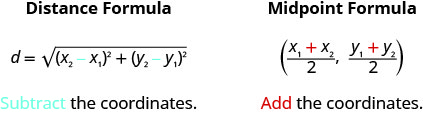
Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

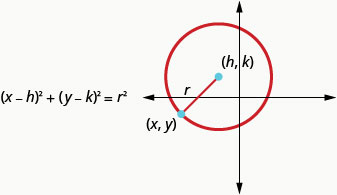
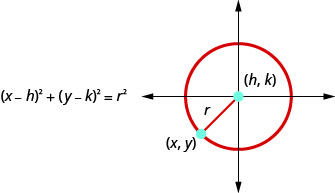
We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

Definition \(\PageIndex{3}\)

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

This is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\).

Definition \(\PageIndex{4}\)

The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is

Example \(\PageIndex{5}\)

Write the standard form of the equation of the circle with radius \(3\) and center \((0,0)\).

Exercise \(\PageIndex{9}\)

Write the standard form of the equation of the circle with a radius of \(6\) and center \((0,0)\).

\(x^{2}+y^{2}=36\)

Exercise \(\PageIndex{10}\)

Write the standard form of the equation of the circle with a radius of \(8\) and center \((0,0)\).

\(x^{2}+y^{2}=64\)

In the last example, the center was \((0,0)\). Notice what happened to the equation. Whenever the center is \((0,0)\), the standard form becomes \(x^{2}+y^{2}=r^{2}\).

Example \(\PageIndex{6}\)

Write the standard form of the equation of the circle with radius \(2\) and center \((−1,3)\).

Exercise \(\PageIndex{11}\)

Write the standard form of the equation of the circle with a radius of \(7\) and center \((2,−4)\).

\((x-2)^{2}+(y+4)^{2}=49\)

Exercise \(\PageIndex{12}\)

Write the standard form of the equation of the circle with a radius of \(9\) and center \((−3,−5)\).

\((x+3)^{2}+(y+5)^{2}=81\)

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example \(\PageIndex{7}\)

Write the standard form of the equation of the circle with center \((2,4)\) that also contains the point \((−2,1)\).

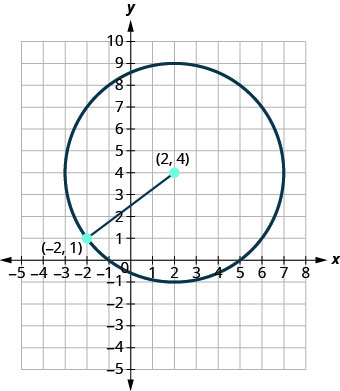
The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center \((2,4)\) and point \((−2,1)\)

Use the Distance Formula to find the radius.

\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Substitute the values. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)

\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)

\(r=\sqrt{(-4)^{2}+(-3)^{2}}\) \(r=\sqrt{16+9}\) \(r=\sqrt{25}\) \(r=5\)

Now that we know the radius, \(r=5\), and the center, \((2,4)\), we can use the standard form of the equation of a circle to find the equation.

Use the standard form of the equation of a circle.

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

Substitute in the values.

\((x-2)^{2}+(y-4)^{2}=5^{2}\)

\((x-2)^{2}+(y-4)^{2}=25\)

Exercise \(\PageIndex{13}\)

Write the standard form of the equation of the circle with center \((2,1)\) that also contains the point \((−2,−2)\).

\((x-2)^{2}+(y-1)^{2}=25\)

Exercise \(\PageIndex{14}\)

Write the standard form of the equation of the circle with center \((7,1)\) that also contains the point \((−1,−5)\).

\((x-7)^{2}+(y-1)^{2}=100\)

Graph a Circle

Any equation of the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) . We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from \(x\) and \(y\). In the next example, the equation has \(x+2\), so we need to rewrite the addition as subtraction of a negative.

Example \(\PageIndex{8}\)

Find the center and radius, then graph the circle: \((x+2)^{2}+(y-1)^{2}=9\).

Exercise \(\PageIndex{15}\)

• Find the center and radius, then
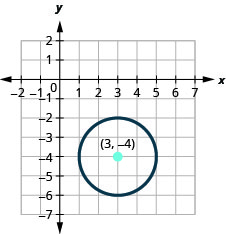
• Graph the circle: \((x-3)^{2}+(y+4)^{2}=4\).
• The circle is centered at \((3,-4)\) with a radius of \(2\).

Exercise \(\PageIndex{16}\)

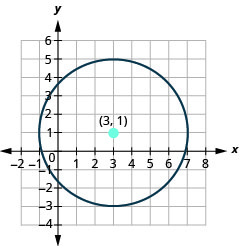
• Graph the circle: \((x-3)^{2}+(y-1)^{2}=16\).
• The circle is centered at \((3,1)\) with a radius of \(4\).

To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of \(x^{2}, y^{2}\) to be one.

Example \(\PageIndex{9}\)

Find the center and radius and then graph the circle, \(4 x^{2}+4 y^{2}=64\).

Exercise \(\PageIndex{17}\)

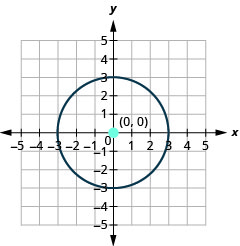
• Graph the circle: \(3 x^{2}+3 y^{2}=27\)
• The circle is centered at \((0,0)\) with a radius of \(3\).

Exercise \(\PageIndex{18}\)

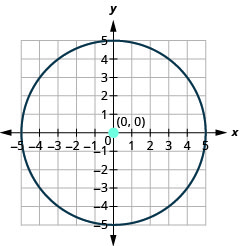
• Graph the circle: \(5 x^{2}+5 y^{2}=125\)
• The circle is centered at \((0,0)\) with a radius of \(5\).

If we expand the equation from Example 11.1.8, \((x+2)^{2}+(y-1)^{2}=9\), the equation of the circle looks very different.

\((x+2)^{2}+(y-1)^{2}=9\)

Square the binomials.

\(x^{2}+4 x+4+y^{2}-2 y+1=9\)

Arrange the terms in descending degree order, and get zero on the right

\(x^{2}+y^{2}+4 x-2 y-4=0\)

This form of the equation is called the general form of the equation of the circle .

Definition \(\PageIndex{5}\)

The general form of the equation of a circle is

\(x^{2}+y^{2}+a x+b y+c=0\)

If we are given an equation in general form, we can change it to standard form by completing the squares in both \(x\) and \(y\). Then we can graph the circle using its center and radius.

Example \(\PageIndex{10}\)

• Graph the circle: \(x^{2}+y^{2}-4 x-6 y+4=0\)

We need to rewrite this general form into standard form in order to find the center and radius.

Exercise \(\PageIndex{19}\)

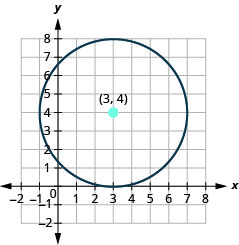
• Graph the circle: \(x^{2}+y^{2}-6 x-8 y+9=0\).
• The circle is centered at \((3,4)\) with a radius of \(4\).

Exercise \(\PageIndex{20}\)

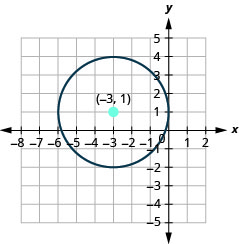
• Graph the circle: \(x^{2}+y^{2}+6 x-2 y+1=0\)
• The circle is centered at \((-3,1)\) with a radius of \(3\).

In the next example, there is a \(y\)-term and a \(y^{2}\)-term. But notice that there is no \(x\)-term, only an \(x^{2}\)-term. We have seen this before and know that it means \(h\) is \(0\). We will need to complete the square for the \(y\) terms, but not for the \(x\) terms.

Example \(\PageIndex{11}\)

• Graph the circle: \(x^{2}+y^{2}+8 y=0\)

Exercise \(\PageIndex{21}\)

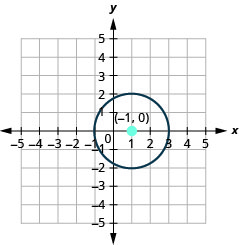
• Graph the circle: \(x^{2}+y^{2}-2 x-3=0\).
• The circle is centered at \((-1,0)\) with a radius of \(2\).

Exercise \(\PageIndex{22}\)

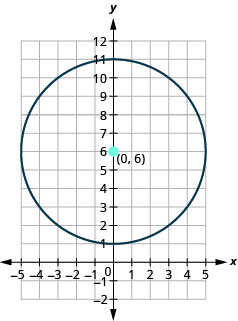
• Graph the circle: \(x^{2}+y^{2}-12 y+11=0\).
• The circle is centered at \((0,6)\) with a radius of \(5\).

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Key Concepts

• Circle: A circle is all points in a plane that are a fixed distance from a fixed point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
• Standard Form of the Equation a Circle: The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) , is

Distance Formula

Learn about the distance formula., distance formula lesson, what is the distance formula.

The distance formula is a way of finding the distance between two points. It does this by creating a virtual right triangle and using the Pythagorean theorem. The distance formula has a 2D (two-dimensional) variation and a 3D (three-dimensional) variation.

The 2D distance formula is given as:

$$\begin{align}& d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{align}$$

The 3D distance formula is given as:

$$\begin{align}& d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + (z_{2} - z_{1})^{2}} \end{align}$$

Where d is the distance between the points, ( x 1 , y 1 , z 1 ) is point 1, and ( x 2 , y 2 , z 2 ) is point 2.

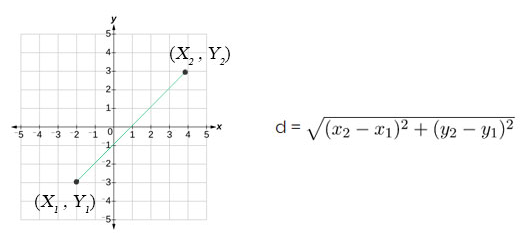
How the Distance Formula Works

The 2D distance formula is the Pythagorean formula applied to two points in the x-y coordinate plane. The first component inside of the square root is (x 2 - x 1 ) 2 . This is the horizontal leg of the right triangle. The second component inside the square root is (y 2 - y 1 ) 2 . This is the vertical leg of the right triangle.

We can visualize the 3D distance formula as a right triangle that happens to reside in the x-y-z 3D coordinate system. Because the two points we are measuring between do not sit flat on a 2D plane, we add in the third term with the variable z . The third term inside of the square root is (z 2 - z 1 ) 2 . It allows the distance between the points to be accurately calculated when they are in 3D space.

2D Distance Formula Example Problem

Find the distance between the points (2, 5) and (7, 3).

$$\begin{align}& \text{1.) The points lie in a 2D system/plane. So, we will use the 2D formula.} \\ \\ & \text{2.) Let's substitute the points into the equation and then simplify.} \\ \\ & \text{3.) } d = \sqrt{(7 - 2)^{2} + (3 - 5)^{2}} \\ \\ & \text{4.) } d = \sqrt{(5)^{2} + (-2)^{2}} \\ \\ & \text{5.) } d = \sqrt{25 + 4} \\ \\ & \text{6.) The distance between the points is: } \; \boxed{d = \sqrt{29}} \end{align}$$

3D Distance Formula Example Problem

Find the distance between the points (1, 4, 11) and (2, 6, 18).

$$\begin{align}& \text{1.) The points are in 3D space, so we will use the 3D distance formula..} \\ \\ & \text{2.) Let's substitute the points into the equation and then simplify.} \\ \\ & \text{3.) } d = \sqrt{(2 - 1)^{2} + (6 - 4)^{2} + (18 - 11)^{2}} \\ \\ & \text{4.) } d = \sqrt{(1)^{2} + (2)^{2} + (7)^{2}} \\ \\ & \text{5.) } d = \sqrt{1 + 4 + 49} \\ \\ & \text{6.) The distance between the points is: } \; \boxed{d = \sqrt{54}} \end{align}$$

Learning math has never been easier. Get unlimited access to more than 168 personalized lessons and 73 interactive calculators. Join Voovers+ Today 100% risk free. Cancel anytime.

Insert/edit link

Enter the destination URL

Or link to existing content

Distance Calculator

What is distance, the distance formula for euclidean distance, distance to any continuous structure, distance to a line and between 2 lines, how to find the distance using our distance calculator, driving distance between cities: a real-world example, distance from earth to moon and sun - astronomical distances, distance beyond length.

Have you ever wanted to calculate the distance from one point to another, or the distance between cities? Have you ever wondered what the distance definition is? We have all these answers and more, including a detailed explanation of how to calculate the distance between any two objects in 2D space. As a bonus, we have a fascinating topic on how we perceive distances (for example as a percentage difference ); we're sure you'll love it!

Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you :

Before we get into how to calculate distances, we should probably clarify what a distance is . The most common meaning is the 1D space between two points. This definition is one way to say what almost all of us think of distance intuitively, but it is not the only way we could talk about distance. You will see in the following sections how the concept of distance can be extended beyond length, in more than one sense that is the breakthrough behind Einstein's theory of relativity.

If we stick with the geometrical definition of distance we still have to define what kind of space we are working in . In most cases, you're probably talking about three dimensions or less, since that's all we can imagine without our brains exploding. For this calculator, we focus only on the 2D distance (with the 1D included as a special case). If you are looking for the 3D distance between 2 points we encourage you to use our 3D distance calculator made specifically for that purpose.

To find the distance between two points, the first thing you need is two points, obviously . These points are described by their coordinates in space. For each point in 2D space, we need two coordinates that are unique to that point. If you wish to find the distance between two points in 1D space you can still use this calculator by simply setting one of the coordinates to be the same for both points . Since this is a very special case, from now on we will talk only about distance in two dimensions.

The next step, if you want to be mathematical, accurate, and precise , is to define the type of space you're working in. No, wait, don't run away! It is easier than you think. If you don't know what space you're working in or if you didn't even know there is more than one type of space, you're most likely working in Euclidean space . Since this is the "default" space in which we do almost every geometrical operation, and it's the one we have set for the calculator to operate on. Let's dive a bit deeper into Euclidean space , what is it, what properties does it have and why is it so important?

The Euclidean space or Euclidean geometry is what we all usually think of 2D space is before we receive any deep mathematical training in any of these aspects. In Euclidean space, the sum of the angles of a triangle equals 180º and squares have all their angles equal to 90º; always. This is something we all take for granted, but this is not true in all spaces . Let's also not confuse Euclidean space with multidimensional spaces. Euclidean space can have as many dimensions as you want, as long as there is a finite number of them, and they still obey Euclidean rules .

We do not want to bore you with mathematical definitions of what is a space and what makes the Euclidean space unique, since that would be too complicated to explain in a simple distance calculator. However, we can try to give you some examples of other spaces that are commonly used and that might help you understand why Euclidean space is not the only space. Also, you will hopefully understand why we are not going to bother calculating distances in other spaces .

The first example we present to you is a bit obscure, but we hope you can excuse us, as we're physicists , for starting with this very important type of space: Minkowski space . The reason we've selected this is because it's very common in physics , in particular it is used in relativity theory, general relativity and even in relativistic quantum field theory. This space is very similar to Euclidean space, but differs from it in a very crucial feature: the addition of the dot product, also called the inner product (not to be confused with the cross product).

Both the Euclidean and Minkowski space are what mathematicians call flat space . This means that space itself has flat properties; for example, the shortest distance between any two points is always a straight line between them (check the linear interpolation calculator). There are, however, other types of mathematical spaces called curved spaces in which space is intrinsically curved and the shortest distance between two points is no a straight line.

This curved space is hard to imagine in 3D, but for 2D we can imagine that instead of having a flat plane area, we have a 2D space, for example, curved in the shape of the surface of a sphere. In this case, very strange things happen . The shortest distance from one point to another is not a straight line, because any line in this space is curved due to the intrinsic curvature of the space. Another very strange feature of this space is that some parallel lines do actually meet at some point . You can try to understand it by thinking of the so-called lines of longitude that divide the Earth into many time zones and cross each other at the poles.

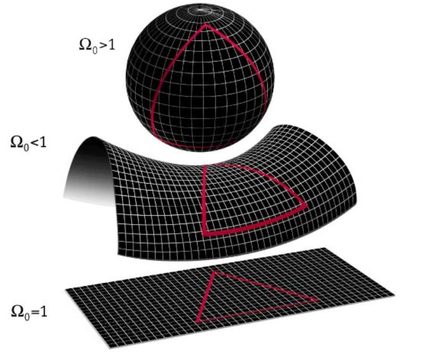
It is important to note that this is conceptually VERY different from a change of coordinates . When we take the standard x , y , z x, y, z x , y , z coordinates and convert into polar, cylindrical, or even spherical coordinates, but we will still be in Euclidean space. When we talk about curved space, we are talking about a very different space in terms of its intrinsic properties . In spherical coordinates, you can still have a straight line and distance is still measured in a straight line, even if that would be very hard to express in numbers.

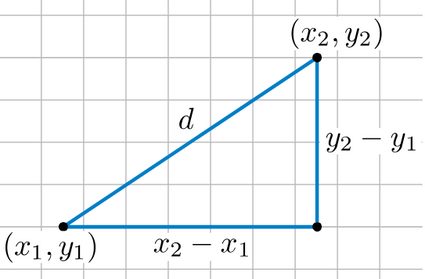
Coming back to the Euclidean space, we can now present you with the distance formula that we promised at the beginning . The distance formula is

which relates to the Pythagorean Theorem, which states that a 2 + b 2 = c 2 a^2+b^2=c^2 a 2 + b 2 = c 2 . Here, a a a and b b b are legs of a right triangle and c c c is the hypotenuse. Suppose that two points, ( x 1 , y 1 ) (x_1, y_1) ( x 1 ​ , y 1 ​ ) and ( x 2 , y 2 ) (x_2, y_2) ( x 2 ​ , y 2 ​ ) , are coordinates of the endpoints of the hypotenuse . Then ( x 2 − x 1 ) 2 (x_2 - x_1)^2 ( x 2 ​ − x 1 ​ ) 2 in the distance equation corresponds to a 2 a^2 a 2 and ( y 2 − y 1 ) 2 (y_2 - y_1)^2 ( y 2 ​ − y 1 ​ ) 2 corresponds to b 2 b^2 b 2 . Since c = a 2 + b 2 c = \sqrt{a^2 + b^2} c = a 2 + b 2 ​ , you can see why this is just an extension of the Pythagorean theorem .

The distance formula we have just seen is the standard Euclidean distance formula , but if you think about it, it can seem a bit limited. We often don't want to find just the distance between two points. Sometimes we want to calculate the distance from a point to a line or to a circle. In these cases, we first need to define what point on this line or circumference we will use for the distance calculation, and then use the distance formula that we have seen just above.

Here is when the concept of perpendicular line becomes crucial. The distance between a point and a continuous object is defined via perpendicularity. From a geometrical point of view, the first step to measure the distance from one point to another, is to create a straight line between both points, and then measure the length of that segment . When we measure the distance from a point to a line, the question becomes "Which of the many possible lines should I draw?". In this case the answer is: the line from the point that is perpendicular to the first line . This distance will be zero in the case in which the point is a part of the line. For these 1D cases, we can only consider the distance between points, since the line represents the whole 1D space .

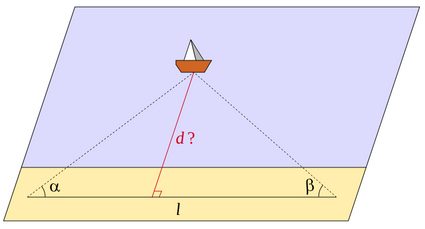
This imposes restrictions on how to compute distances in some interesting geometrical instances. For example, we could redefine the concept of height of a triangle to be simply the distance from one vertex to the opposing side of the triangle. In this case, the triangle area is also redefined in terms of distance, since the area is a function of the height of the triangle.

Let's look at couple examples in 2D space. To calculate the distance between a point and a straight line we could go step by step (calculate the segment perpendicular to the line from the line to the point and the compute its length) or we could simply use this 'handy-dandy' equation :

where the line is given by A x + B y + C = 0 Ax+By+C = 0 A x + B y + C = 0 and the point is defined by ( x 1 , y 1 ) (x_1, y_1) ( x 1 ​ , y 1 ​ ) .

The only problem here is that a straight line is generally given as y = m x + b y=mx+b y = m x + b , so we would need to convert this equation to the previously show form:

so we can see that A = m A=m A = m , B = − 1 B=-1 B = − 1 and C = b C=b C = b . This leaves the previous equation with the following values:

For the distance between 2 lines, we just need to compute the length of the segment that goes from one to the other and is perpendicular to both. Once again, there is a simple formula to help us :

if the lines are A 1 x + B 1 y + C 1 = 0 A_1x+B_1y+C_1=0 A 1 ​ x + B 1 ​ y + C 1 ​ = 0 and A 2 x + B 2 y + C 2 = 0 A_2x+B_2y+C_2=0 A 2 ​ x + B 2 ​ y + C 2 ​ = 0 . We can also convert to slope intercept form and obtain:

for lines y = m 1 x + b 1 y=m_1x+b_1 y = m 1 ​ x + b 1 ​ and y = m 2 x + b 2 y=m_2x+b_2 y = m 2 ​ x + b 2 ​ .

Notice that both line needs to be parallel since otherwise the would touch at some point and their distance would then be d = 0 d=0 d = 0 . That's the reason the formulas omit most of the subscripts since for parallel lines: A 1 = A 2 = A A_1=A_2=A A 1 ​ = A 2 ​ = A and B 1 = B 2 = B B_1=B_2=B B 1 ​ = B 2 ​ = B while in slope intercept form parallel lines are those for which m 1 = m 2 = m m_1=m_2=m m 1 ​ = m 2 ​ = m .

As we have mentioned before, distance can mean many things , which is why we have provided a few different options for you in this calculator. You can calculate the distance between a point and a straight line, the distance between two straight lines (they always have to be parallel), or the distance between points in space. When it comes to calculating the distances between two point, you have the option of doing so in 1, 2, 3, or 4 dimensions. We know, we know, 4 dimensions sounds scary , but you don't need to use that option. And you can always learn more about it by reading some nice resources and playing around with the calculator. We promise it won't break the Internet or the universe.

We have also added the possibility for you to define 3 different points in space, from which you will obtain the 3 pairs of distances between them, so, if you have more than two points, this will save you time. The number of dimensions you are working in will determine the number of coordinates that describe a point, which is why, as you increase the number of dimensions, the calculator will ask for more input values.

Even though using the calculator is very straightforward, we still decided to include a step-by-step solution. This way you can get acquainted with the distance formula and how to use it (as if this was the 1950's and the Internet was still not a thing). Now let's take a look at a practical example: How to find the distance between two points in 2-D.

Suppose you have two coordinates, ( 3 , 5 ) (3, 5) ( 3 , 5 ) and ( 9 , 15 ) (9, 15) ( 9 , 15 ) , and you want to calculate the distance between them. To calculate the 2-D distance between these two points, follow these steps:

• Input the values into the formula: ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} ( x 2 ​ − x 1 ​ ) 2 + ( y 2 ​ − y 1 ​ ) 2 ​ .
• In the formula, subtract the values in the parentheses.
• Square both quantities in the parentheses.
• Add the results.
• Take the square root.
• Use the distance calculator to check your results.

Working out the example by hand, you get:

which is equal to approximately 11.66 11.66 11.66 . Note, that when you take the square root, you will get a positive and negative result, but since you are dealing with distance, you are only concerned with the positive result . The calculator will go through this calculations step by step to give you the result in exact and approximate formats.

Let's take a look of one of the applications of the distance calculator. Suppose you are traveling between cities A and B, and the only stop is in city C, with a route A to B perpendicular to route B to C. We can determine the distance from A to B, and then, knowing the gas price, determine fuel cost , fuel used and cost per person while traveling. The gas calculator, that you can find on our site, can ease that for you.

The difficulty here is to calculate the distances between cities accurately . A straight line (like what we use in this calculator) can be a good approximation, but it can be quite off if the route you're taking is not direct but takes some detour, maybe to avoid mountains or to pass by another city. In that case, just use Google maps or any other tool that calculates the distance along a path not just the distance from one point to another as the crow flies.

Our calculator can give proper measurements and predictions for distances between objects, not the length of a path . With this in mind, there are still multiple scenarios in which you might actually be interested in the distance between objects, regardless of the path you would have to take. One such example is the distance between astronomical objects .

When we look at a distance within our Earth, it is hard to go far without bumping into some problems , from the intrinsic curvature of this space (due to the Earth curvature being non-zero) to the limited maximum distance between two points on the Earth. It is because of this, and also because there is a whole universe beyond our Earth , that distances in the universe are of big interest for many people. Since we have no proper means of interplanetary traveling, let alone interstellar travels, let's focus for now on the actual Euclidean distance to some celestial objects. For example the distance from the Earth to the Sun, or the distance from the Earth to the Moon.

These distances are beyond imaginable for our ape-like brains. We struggle to comprehend the size of our planet, never mind the vast, infinite universe. This is so difficult that we need to use either scientific notation or light years, as a unit of distance for such long lengths . The longest trips you can do on Earth are barely a couple thousand kilometers, while the distance from Earth to the Moon, the closest astronomical object to us, is 384,000 km . On top of that, the distance to our closest star, that is the distance from Earth to the Sun , is 150,000,000 km or a little over 8 light minutes .

When you compare these distances with the distance to our second nearest star (Alpha Centauri) , which is 4 light years , suddenly they start to look much smaller. If we want to go even more ridiculous in comparison we can always think about a flight from New York to Sydney, which typically takes more than 20 h and it's merely over 16,000 km , and compare it with the size of the observable universe, which is about 46,600,000,000 light years !

Here, we have inadvertently risen a fascinating point , which is that we measure distances not in length but in time. Thus, we extend the notion of distance beyond its geometrical sense. We will explore this possibility in the next section as we speak about the importance and usefulness of distance beyond the purely geometrical sense . This is a very interesting path to take and is mostly inspired by the philosophical need to extend every concept to have a universal meaning, as well as from the obvious physical theory to mention, when talking about permutations of the space and time, or any other variable that can be measured .

Typically, the concept of distance refers to the geometric Euclidean distance and is linked to length. However, you can extend the definition of distance to mean just the difference between two things , and then a world of possibilities opens up. Suddenly one can decide what is the best way to measure the distance between two things and put it in terms of the most useful quantity. A very simple step to take is to think about the distance between two numbers, which is nothing more than the 1D difference between these numbers . To obtain it, we simply subtract one from the other and the result would be the difference, a.k.a. the distance.

We could jump from this numerical distance to, for example, difference or distance in terms of the percentage difference, which in some cases might provide a better way of comparison . This is still just one level of abstraction in which we simply remove the units of measurement. But what if we were to use different units altogether?

By extending the concept of distance to mean something closer to difference , we can calculate the difference between two temperatures, or other related quantity like pressure. But we don't need to get really extreme, let's see how two points can be separated by a different distance, depending on the assumptions made . Coming back to the driving distance example, we could measure the distance of the journey in time, instead of length. In this case, we need an assumption to allow such translation; namely the way of transport.

There is a big difference in the time taken to travel 10 km by plane versus the time it takes by car . Sometimes, however, the assumption is clear and implicitly agreed on, like when we measure the lightning distance in time which we then convert to length. This brings up an interesting point, that the conversion factor between distances in time and length is what we call "speed" or "velocity" (remember they are not exactly the same thing). Truth be told, this speed doesn't have to be constant as exemplified by accelerated motions such as that of a free fall under gravitational force, or the one that links stopping time and stopping distance via the breaking force and drag or, in very extreme cases, via the force of a car crash.

Another place where you can find weird units of distance are in solid state physics, where the distance a particle travels inside of a material is often expressed as an average of interactions or collisions. This distance is linked to length by using the mean free path, which is the mean distance (in length) a particle travels between interactions. If we want to get even more exotic we can think about the distance from the present value to the future value of something like a car.

We don't want to, however, make anyone's brain explode, so please don't think too hard about this . Just take this calculator and use it for length-based distance in 2D space. You can always return to this philosophical view on distances if you ever find yourself bored!

How to find the distance between two points?

To find the distance between two points we will use the distance formula: √[(x₂ - x₁)² + (y₂ - y₁)²]:

• Get the coordinates of both points in space.
• Subtract the x-coordinates of one point from the other, same for the y components.
• Square both results separately.
• Sum the values you got in the previous step.
• Find the square root of the result above.

If you think this is too much effort, you can simply use the Distance Calculator from Omni

Is distance a vector?

Distance is not a vector . The distance between points is a scalar quantity, meaning it is only defined by its value. However, the displacement is a vector with value and direction. So the distance between A and B is the same as the distance from B to A, but the displacement is different depending on their order.

What is a klick in distance?

Click is slang for a kilometer which is 0.62 miles. It is actually written with "k" (Klick) as it is derived from the word kilometer. It is commonly used in the military and motorcyclists.

What is the distance formula?

The distance formula is: √[(x₂ - x₁)² + (y₂ - y₁)²] . This works for any two points in 2D space with coordinates (x₁, y₁) for the first point and (x₂, y₂) for the second point. You can memorize it easily if you notice that it is Pythagoras theorem and the distance is the hypothenuse, and the lengths of the catheti are the difference between the x and y components of the points.

How to find the distance of a vector?

The distance of a vector is its magnitude . If you know its components:

• Take each of the components of the vector and square them.
• Sum them up.
• Find the square root of the previous result.
• Enjoy the good work!

If you know its polar representation , it will be a number and an angle. That number is the magnitude of the vector, which is its distance.

What is the SI unit of distance?

The SI unit of distance is the meter , abbreviated to "m". A meter is approximately 3.28 feet. Other common units in the International System of units are the centimeter (one one-hundredth of a meter, or 0.39 inches) and the kilometer (one thousand meters or 0.62 miles), among others.

What is the distance from A to B?

The distance from A to B is the length of the straight line going from A to B. The distance from B to A is the same as the distance from A to B because distance is a scalar

What is the dimension of distance?

Distance is a measure of one-dimensional space. The distance between two points is the shortest length of 1D space between them. If you divide distance over time you will get speed, which has dimensions of space over time.

Is light-year time or distance?

A light-year is a measurement of distance. It is 9.461×10 12 kilometers or 5.879×10 12 miles, which is the distance traveled by a ray of light in a perfect vacuum over the span of a year.

How to solve for distance with velocity and time?

The velocity and the moving time of an object you can calculate the distance:

• Make sure the speed and time have compatible units (miles per hour and hours, meter per second, and seconds…).
• If they aren't, convert them to the necessary units.
• Multiply the velocity by the time .
• The result should be the distance traveled in whichever length units your speed was using!

Harmonic number

Ideal egg boiling, surface area of a rectangle.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

Algebra: Distance Problems

In these lessons, we will learn to solve word problems involving distance, rate (speed) and time.

Related Pages Rate Distance Time Word Problems Distance Word Problems Average Speed Problems

What Are Distance Word Problems Or Distance Rate Time Problems?

Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time .

The formula for distance problems is: distance = rate × time or d = r × t

Things to watch out for: Make sure that you change the units when necessary. For example, if the rate is given in miles per hour and the time is given in minutes then change the units appropriately.

It would be helpful to use a table to organize the information for distance problems. A table helps you to think about one number at a time instead being confused by the question.

The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page for examples and solutions.

We will show you how to solve distance problems by the following examples:

• Traveling At Different Rates
• Traveling In Different Directions
• Given Total Time
• Wind and Current Problems

How To Solve Distance Problems: Traveling At Different Rates

Example: A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Solution: Step 1: Set up a rtd table.

Step 2: Fill in the table with information given in the question.

A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Let t = time to make the trip in Case 2.

Step 3: Fill in the values for d using the formula d = rt

Step 4: Since the distances traveled in both cases are the same, we get the equation:

Step 5: Beware - the question asked for “how many more minutes would it have taken to make the trip”, so we need to deduct the original 6 hours taken.

Answer: The time taken would have been 40 minutes longer.

How To Solve Distance Problems: Two Objects Traveling In The Same Direction

Example: This motion problem (or distance rate time problem or uniform rate problem) involves traveling in the same direction, solving for “how long” one moving object traveling until it meets up with the second moving object.

It uses d = rt (distance equals rate times time).

Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the same point A and heads for point B at 75 mph. How long before car 2 overtakes car 1?

How To Solve Distance Problems: Two Objects Traveling In The Opposite Directions

Example: A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

Let t = time when they are 210 miles apart.

Step 4: Since the total distance is 210, we get the equation:

50t + 55t = 210 105t = 210

Answer: They will be 210 miles apart in 2 hours.

Objects Traveling At Opposite Directions, Calculate How Long It Takes For Them To Be A Given Distance Apart

This motion problem (or distance rate time problem or uniform rate problem) involves one object traveling in one direction and the other in the opposite direction, solving for “how long” (or the amount of time) two moving objects traveling until they are certain distance apart.

Example: Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?

How To Solve Distance Problems: Given The Total Time

Example: John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?

John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?

Let t = time to travel to town.

7 – t = time to return from town.

40t = 30(7 – t) Use distributive property 40t = 210 – 30t

Step 5: The distance traveled by John to town is

40t = 120 The distance traveled by John to go back is also 120 So, the total distance traveled by John is 240

Answer: The distance traveled by John is 240 miles.

How To Find The Total Distance Given Total Time And Two Rates?

Example: Roy took 5 hours to complete a journey. For the first 2 hours, he traveled at an average speed of 65 km/h. For the rest of the journey, he traveled at an average speed of 78 km/h. What was the total distance of the journey?

How To Solve Wind And Current Word Problems?

There is another group of distance-time problems that involves the speed of the water current or the speed of wind affecting the speed of the vehicle. The following video shows an example of such a problem.

How to solve Wind Word Problems?

Example: Into the headwind, the plane flew 2000 miles in 5 hours. With a tailwind, the return trip took 4 hours. Find the speed of the plane in still air and the speed of the wind.

How to find the speed of the current of a stream?

Example: The speed of a boat in still water is 10 mph. It travels 24 miles upstream and 24 miles downstream in 5 hours. What is the speed of the current?

How to solve Current Word Problems?

Example: Traveling downstream, Elmo can go 6 km in 45 minutes. On the return trip, it takes him 1.5 hours. What is the boat’s speed in still water and what is the rate of the current?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

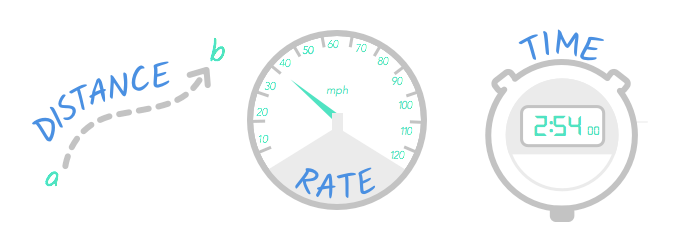
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

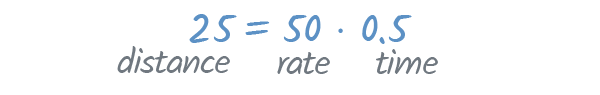
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

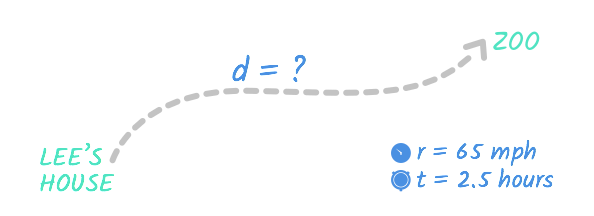
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

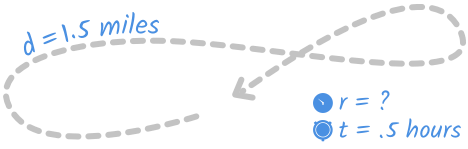
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

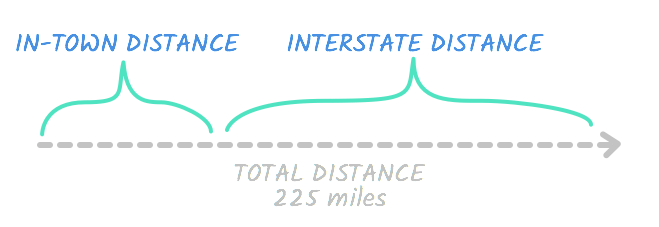
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

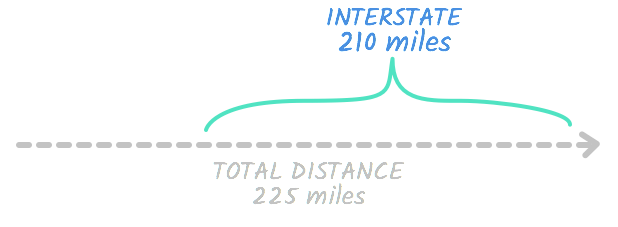
So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

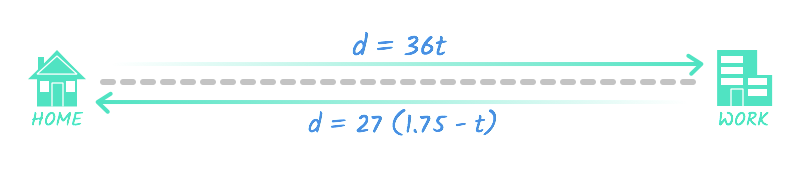
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

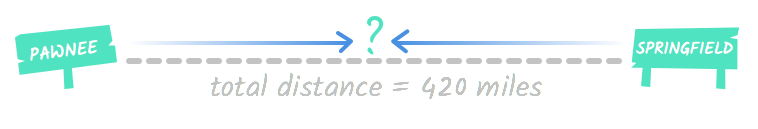
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

• Problems on Distance Formula

We will discuss here how to solve the problems on distance formula.

The distance between two points A (x\(_{1}\), y\(_{1}\)) and B (x\(_{2}\), y\(_{2}\)) is given by the formula

AB = \(\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}\)

1.  If the distance between the points (5, - 2) and (1, a) is 5, find the values of a.

We know, the distance between (x\(_{1}\), y\(_{1}\)) and (x\(_{2}\), y\(_{2}\))

is \(\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}\)

Here, the distance = 5, x\(_{1}\) = 5, x\(_{2}\) = 1, y\(_{1}\) = -2 and y\(_{2}\) = a

Therefore, 5 = \(\sqrt{(5 - 1)^{2} + (-2 - a)^{2}}\)

⟹ 25 = 16 + (2 + a)\(^{2}\)

⟹ (2 + a)\(^{2}\) = 25 - 16

⟹ (2 + a)\(^{2}\) = 9

Taking square root, 2 + a = ±3

⟹ a = -2 ± 3

⟹ a = 1, -5

2. The co-ordinates of points on the x-axis which are at a distance of 5 units from the point (6, -3).

Let the co-ordinates of the point on the x-axis be (x, 0)

Since, distance = \(\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}\)

Now taking (6, -3) = (x\(_{1}\), y\(_{1}\)) and (x, 0) = (x\(_{2}\), y\(_{2}\)), we get

5 = \(\sqrt{(x - 6)^{2} + (0 + 3)^{2}}\)

Squaring both sides we get

⟹ 25 = (x – 6)\(^{2}\) + 3\(^{2}\)

⟹ 25 = x\(^{2}\) – 12x + 36 + 9

⟹ 25 = x\(^{2}\) – 12x + 45

⟹ x\(^{2}\) – 12x + 45 – 25 = 0

⟹ x\(^{2}\) – 12x + 20 = 0

⟹ (x – 2)(x – 10) = 0

⟹ x = 2 or x = 10

Therefore, the required points on the x-axis are (2, 0) and (10, 0).

3. Which point on the y-axis is equidistance from the points (12, 3) and (-5, 10)?

Let the required point on the y-axis (0, y).

Given (0, y) is equidistance from (12, 3) and (-5, 10)

i.e., distance between (0, y) and (12, 3) = distance between (0, y) and (-5, 10)

⟹ \(\sqrt{(12 - 0)^{2} + (3 - y)^{2}}\) = \(\sqrt{(-5 - 0)^{2} + (10 - y)^{2}}\)

⟹ 144 + 9 + y\(^{2}\) – 6y = 25 + 100 + y\(^{2}\) – 20y

⟹ 14y = -28

Therefore, the required point on the y-axis = (0, -2)

4.  Find the values of a such that PQ = QR, where P, Q and R are the points whose coordinates are (6, - 1), (1, 3) and (a, 8) respectively.

PQ = \(\sqrt{(6 - 1)^{2} + (-1 - 3)^{2}}\)

     = \(\sqrt{5^{2} + (-4)^{2}}\)

     = \(\sqrt{25 + 16}\)

     = \(\sqrt{41}\)

QR = \(\sqrt{(1 - a)^{2} + (3 - 8)^{2}}\)

     = \(\sqrt{(1 - a)^{2} + (-5)^{2}}\)

     = \(\sqrt{(1 - a)^{2} + 25}\)

Therefore, PQ = QR

⟹ \(\sqrt{41}\) = \(\sqrt{(1 - a)^{2} + 25}\)

⟹ 41 = (1 - a)\(^{2}\) + 25

⟹ (1 - a)\(^{2}\) = 41 - 25

⟹ (1 - a)\(^{2}\) = 16

⟹ 1 - a = ±4

⟹ a = -3, 5

5.  Find the points on the y-axis, each of which is at a distance of 13 units from the point (-5, 7).

Let A (-5, 7) be the given point and let P (0, y) be the required point on the y-axis. Then,

PA = 13 units

⟹ PA\(^{2}\) = 169

⟹ (0 + 5)\(^{2}\) + (y - 7)\(^{2}\) = 169

⟹ 25 + y\(^{2}\) - 14y + 49 = 169

⟹ y\(^{2}\) – 14y + 74 = 169

⟹ y\(^{2}\) – 14y – 95 = 0

⟹ (y - 19)(y + 5) = 0

⟹ y – 19 = 0 or, y + 5 = 0

⟹ y = 19 or, y = -5

Hence, the required points are (0, 19) and (0, -5)

●   Distance and Section Formulae

• Distance Formula
• Distance Properties in some Geometrical Figures
• Conditions of Collinearity of Three Points
• Distance of a Point from the Origin
• Distance Formula in Geometry
• Section Formula
• Midpoint Formula
• Centroid of a Triangle
• Worksheet on Distance Formula
• Worksheet on Collinearity of Three Points
• Worksheet on Finding the Centroid of a Triangle
• Worksheet on Section Formula

10th Grade Math From Problems on Distance Formula to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer

Apr 24, 24 03:46 PM

Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry

Apr 24, 24 03:45 PM

Mental Math on Geometrical Shapes | Geometry Worksheets| Answer

Apr 24, 24 03:35 PM

Circle Math | Terms Related to the Circle | Symbol of Circle O | Math

Apr 24, 24 02:57 PM

Fundamental Geometrical Concepts | Point | Line | Properties of Lines

Apr 24, 24 12:38 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Module 9: Multi-Step Linear Equations

Using the distance, rate, and time formula, learning outcomes.

• Use the problem-solving method to solve problems using the distance, rate, and time formula

One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you traveled if you drove at a steady rate of [latex]60[/latex] miles per hour for [latex]2[/latex] hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said [latex]120[/latex] miles, you already know how to use this formula!

The math to calculate the distance might look like this:

[latex]\begin{array}{}\\ \text{distance}=\left(\Large\frac{60\text{ miles}}{1\text{ hour}}\normalsize\right)\left(2\text{ hours}\right)\hfill \\ \text{distance}=120\text{ miles}\hfill \end{array}[/latex]

In general, the formula relating distance, rate, and time is

[latex]\text{distance}\text{=}\text{rate}\cdot \text{time}[/latex]

Distance, Rate, and Time

For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula

[latex]d=rt[/latex]

where [latex]d=[/latex] distance, [latex]r=[/latex] rate, and [latex]t=[/latex] time.

Notice that the units we used above for the rate were miles per hour, which we can write as a ratio [latex]\Large\frac{miles}{hour}[/latex]. Then when we multiplied by the time, in hours, the common units “hour” divided out. The answer was in miles.

Jamal rides his bike at a uniform rate of [latex]12[/latex] miles per hour for [latex]3\Large\frac{1}{2}[/latex] hours. How much distance has he traveled?

In the following video we provide another example of how to solve for distance given rate and time.

Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of [latex]520[/latex] miles. If he can drive at a steady rate of [latex]65[/latex] miles per hour, how many hours will the trip take?

Show Solution

In the following video we show another example of how to find rate given distance and time.

• Question ID 145550, 145553,145619,145620. Authored by : Lumen Learning. License : CC BY: Attribution
• Ex: Find the Rate Given Distance and Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/3rYh32ErDaE . License : CC BY: Attribution
• Example: Solve a Problem using Distance = Rate x Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/lMO1L_CvH4Y . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Distance Formula Problems

Find the distance between two points using the distance formula.

1. Substitute the x- and y-coordinates into the distance formula

2. Solve using order of operations.

Use the distance formula to find the distance between X(-7, 5) and Y(2, -6). Round the answer to the nearest tenth.

Substitute the x- and y-coordinates into the distance formula.

Practice Distance Formula Problems

Practice Problem 1

Practice Problem 2

Practice Problem 3

Distance  is a numerical measurement of how far apart objects or points are. The distance between two points is the length of a straight line segment that links them.

Pre-requisite Skills Pythagorean Theorem Applications of the Pythagorean Theorem

Related Skills Graph Points on Coordinate Plane Graph Objects on a Coordinate Plane

Solving Problems Involving Distance, Rate, and Time

• Pre Algebra & Algebra
• Math Tutorials
• Exponential Decay
• Worksheets By Grade

In math, distance, rate, and time are three important concepts you can use to solve many problems if you know the formula. Distance is the length of space traveled by a moving object or the length measured between two points. It is usually denoted by d in math problems .

The rate is the speed at which an object or person travels. It is usually denoted by  r  in equations . Time is the measured or measurable period during which an action, process, or condition exists or continues. In distance, rate, and time problems, time is measured as the fraction in which a particular distance is traveled. Time is usually denoted by t in equations. 

Solving for Distance, Rate, or Time

When you are solving problems for distance, rate, and time, you will find it helpful to use diagrams or charts to organize the information and help you solve the problem. You will also apply the formula that solves distance, rate, and time, which is  distance = rate x tim e. It is abbreviated as:

There are many examples where you might use this formula in real life. For example, if you know the time and rate a person is traveling on a train, you can quickly calculate how far he traveled. And if you know the time and distance a passenger traveled on a plane, you could quickly figure the distance she traveled simply by reconfiguring the formula.

Distance, Rate, and Time Example

You'll usually encounter a distance, rate, and time question as a word problem in mathematics. Once you read the problem, simply plug the numbers into the formula.

For example, suppose a train leaves Deb's house and travels at 50 mph. Two hours later, another train leaves from Deb's house on the track beside or parallel to the first train but it travels at 100 mph. How far away from Deb's house will the faster train pass the other train?

To solve the problem, remember that d represents the distance in miles from Deb's house and t  represents the time that the slower train has been traveling. You may wish to draw a diagram to show what is happening. Organize the information you have in a chart format if you haven't solved these types of problems before. Remember the formula:

distance = rate x time

When identifying the parts of the word problem, distance is typically given in units of miles, meters, kilometers, or inches. Time is in units of seconds, minutes, hours, or years. Rate is distance per time, so its units could be mph, meters per second, or inches per year.

Now you can solve the system of equations:

50t = 100(t - 2) (Multiply both values inside the parentheses by 100.) 50t = 100t - 200 200 = 50t (Divide 200 by 50 to solve for t.) t = 4

Substitute t = 4 into train No. 1

d = 50t = 50(4) = 200

Now you can write your statement. "The faster train will pass the slower train 200 miles from Deb's house."

Sample Problems

Try solving similar problems. Remember to use the formula that supports what you're looking for—distance, rate, or time.

d = rt (multiply) r = d/t (divide) t = d/r (divide)

Practice Question 1

A train left Chicago and traveled toward Dallas. Five hours later another train left for Dallas traveling at 40 mph with a goal of catching up with the first train bound for Dallas. The second train finally caught up with the first train after traveling for three hours. How fast was the train that left first going?

Remember to use a diagram to arrange your information. Then write two equations to solve your problem. Start with the second train, since you know the time and rate it traveled:

Second train t x r = d 3 x 40 = 120 miles First train t x r = d 8 hours x r = 120 miles Divide each side by 8 hours to solve for r. 8 hours/8 hours x r = 120 miles/8 hours r = 15 mph

Practice Question 2

One train left the station and traveled toward its destination at 65 mph. Later, another train left the station traveling in the opposite direction of the first train at 75 mph. After the first train had traveled for 14 hours, it was 1,960 miles apart from the second train. How long did the second train travel? First, consider what you know:

First train r = 65 mph, t = 14 hours, d = 65 x 14 miles Second train r = 75 mph, t = x hours, d = 75x miles

Then use the d = rt formula as follows:

d (of train 1) + d (of train 2) = 1,960 miles 75x + 910 = 1,960 75x = 1,050 x = 14 hours (the time the second train traveled)

• Distance, Rate, and Time Worksheets
• What Is Velocity in Physics?
• Realistic Math Problems Help 6th-graders Solve Real-Life Questions
• 4th-Grade Math Word Problems
• Circumference of a Circle
• What Speed Actually Means in Physics
• Understanding the Distance Formula
• Help Kids Calculate the Area and Circumference of Circles
• How to Calculate Commissions Using Percents
• Rate of Change Worksheet with Solutions
• How to Derive the Formula for Combinations
• How to Determine the Geometry of a Circle
• Dimensional Analysis: Know Your Units
• Problem Solving in Mathematics
• Perimeter and Surface Area Formulas
• The Arrhenius Equation Formula and Example

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Master Motion: A Comprehensive Guide to Understanding the Distance Formula in Real-World Problems

Understanding motion and work problems, especially those involving the formula \(d=rt\) (where \(d\) stands for distance, \(r\) for rate, and \(t\) for time), can be simplified through a step-by-step guide:

A step-by-step guide to Master Motion

Step 1: understanding the formula.

• Formula : \(d=rt\).
• Distance (\(d\)) : This represents the total distance traveled.
• Rate (\(r\)) : This is the speed or velocity at which an object moves. It’s expressed as a distance per unit of time (like miles per hour or kilometers per hour).
• Time (\(t\)) : The duration for which the object has been moving.

Step 2: Consistency in Units

• Importance of Consistent Units : It’s crucial to ensure that the units of rate and time match. For example, if the rate is in miles per hour, time should be in hours, not minutes.
• Converting Units : If units do not match, convert them. For instance, if time is given in minutes and rate in hours, convert time to hours by dividing by \(60\).

Step 3: Solving for Any Variable

• Solving for Distance (\(d\)) : If rate and time are known, multiply them to find the distance.
• Solving for Rate (\(r\)) : If distance and time are known, divide the distance by time to find the rate.
• Solving for Time (\(t\)) : If distance and rate are known, divide the distance by rate to find the time.

Step 4: Application in Problems

• Problem Analysis : Identify what is being asked, what is given, and what is unknown.
• Assign Variables : Assign the given values to their respective variables in the formula.
• Solve : Perform the necessary calculations to find the unknown value.

Step 5: Common Mistakes to Avoid

• Not Converting Units : One of the most common mistakes is not converting units to ensure they are consistent.
• Ignoring Decimal Places : Be precise with calculations, especially when dealing with decimals.
• Misreading the Problem : Carefully read what is asked to correctly identify the known and unknown variables.

Step 6: Practice and Application

• Practice Problems : Regularly solve different types of motion problems to get a better grasp of the concept.
• Real-Life Application : Apply these concepts to everyday situations like calculating travel time for a trip or the speed of a vehicle.

By following these steps and practicing regularly, understanding motion and work problems, especially those related to the distance formula \(d=rt\), becomes more manageable and intuitive.

Example 1 :

A car travels at a speed of \(50\) miles per hour. How far will it travel in \(3\) hours?

\(Distance = Rate × Time = 50 \ \frac{miles}{hour} × 3 \ hours = 150 \ miles\).

Example 2 :

A cyclist covers a distance of \(90\) kilometers in \(3\) hours. What is the cyclist’s average speed?

\(Speed = Distance ÷ Time = 90 \ km ÷ 3 \ hours = 30 \frac{km}{hour}\).

by: Effortless Math Team about 5 months ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• How to Write the Standard Form of Linear Equations?
• How to Find Magnitude of Vectors?
• Full-Length 8th Grade ACT Aspire Math Practice Test
• 5th Grade M-STEP Math Worksheets: FREE & Printable
• 10 Most Common 3rd Grade PARCC Math Questions
• How to Multiply Three or More Mixed Numbers, Fractions & Whole Numbers?
• How to Develop a Mindset for Math in 7 Steps?
• A Comprehensive Collection of Free TASC Math Practice Tests
• 7th Grade MEAP Math FREE Sample Practice Questions
• How to Solve Real-Life Puzzles: Word Problems on Adding and Subtracting Fractions with Like Denominators

What people say about "How to Master Motion: A Comprehensive Guide to Understanding the Distance Formula in Real-World Problems - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems, algebra i study guide a comprehensive review and step-by-step guide to preparing for algebra i, oar math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the oar math, act math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the act math, pre-algebra study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the pre-algebra, tsi math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the tsi math, tabe 11 & 12 math study guide 2020 – 2021 for level d a comprehensive review and step-by-step guide to preparing for the tabe math, ftce math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ftce general knowledge math, ged math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ged math.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Distance Formula

Distance formula calculator

How it works:  Type the two x coordinates and two y coordinates into the boxes below and it will automatically calculate the distance between those 2 points and show you step by step.

Distance between two points

In a Cartesian grid, to measure a line segment that is either vertical or horizontal is simple enough. You can count the distance either up and down the y-axis or across the x-axis.

But what about diagonal lines? How can you know precisely how long the line segment is if it cuts across those tiny boxes? See this example:

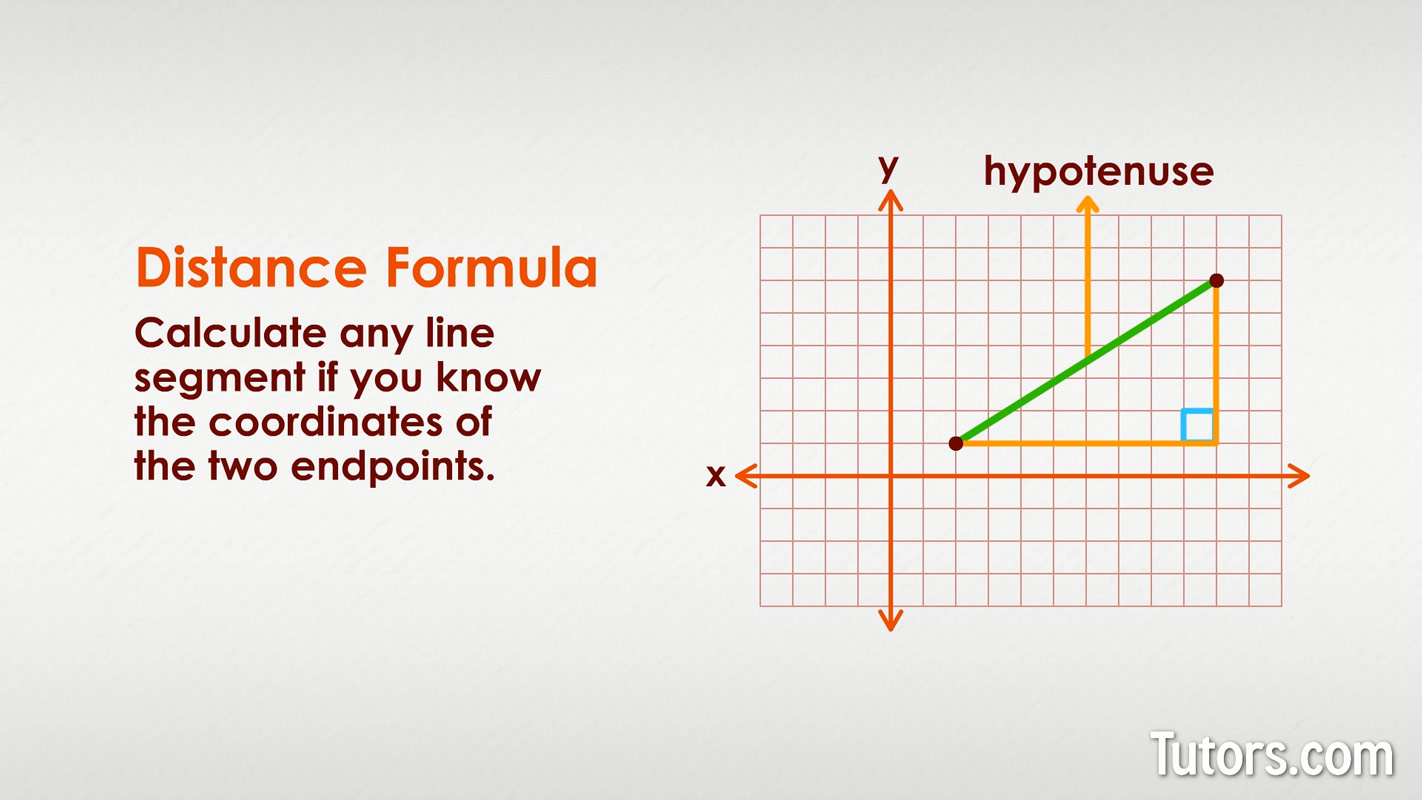
You can use the distance formula to calculate any line segment if you know the coordinates of the two endpoints. You will be mentally constructing a right triangle, using the diagonal as if it were a hypotenuse.

Distance formula

The  Distance Formula  squares the differences between the two x coordinates and two y coordinates, then adds those squares, and finally takes their square root to get the total distance along the diagonal line:

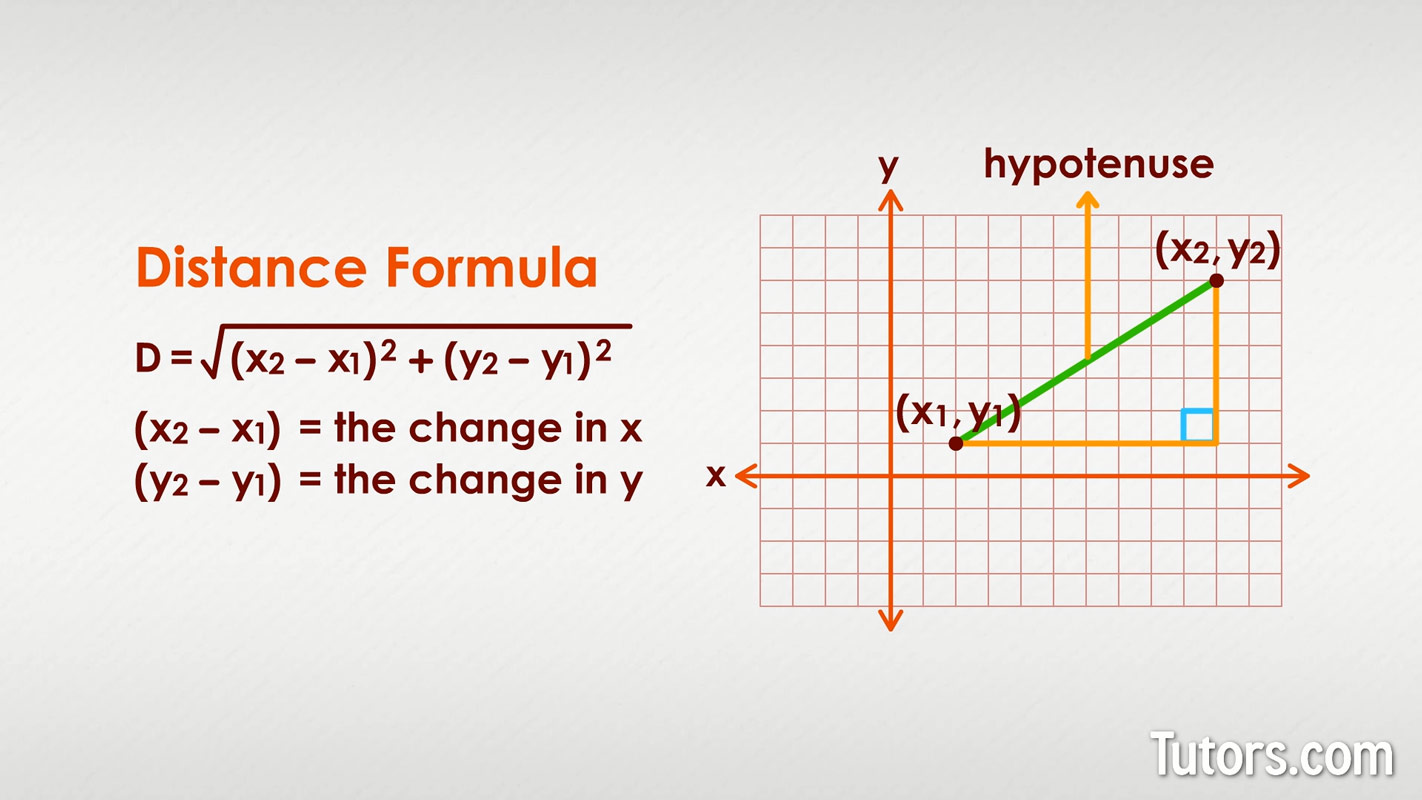
The expression ( x 2 − x 1 ) ({x}_{2}-{x}_{1}) ( x 2 ​ − x 1 ​ )  is read as  the change in x  and  ( y 2 − y 1 ({y}_{2}-{y}_{1} ( y 2 ​ − y 1 ​  is  the change in y .

How to use the distance formula

What this is really doing is calculating the distance horizontally between x- values , as if a line segment was forming a side of a right triangle, and then doing that again with the y -values , as if a vertical line segment was the second side of a right triangle.

That leaves a calculation about the hypotenuse, your given diagonal. The distance formula is a special application of the Pythagorean theorem .

All you need to do is plug the coordinates in very carefully. Let's use our line's endpoints,  (1, 3)  and  (7, 6) :

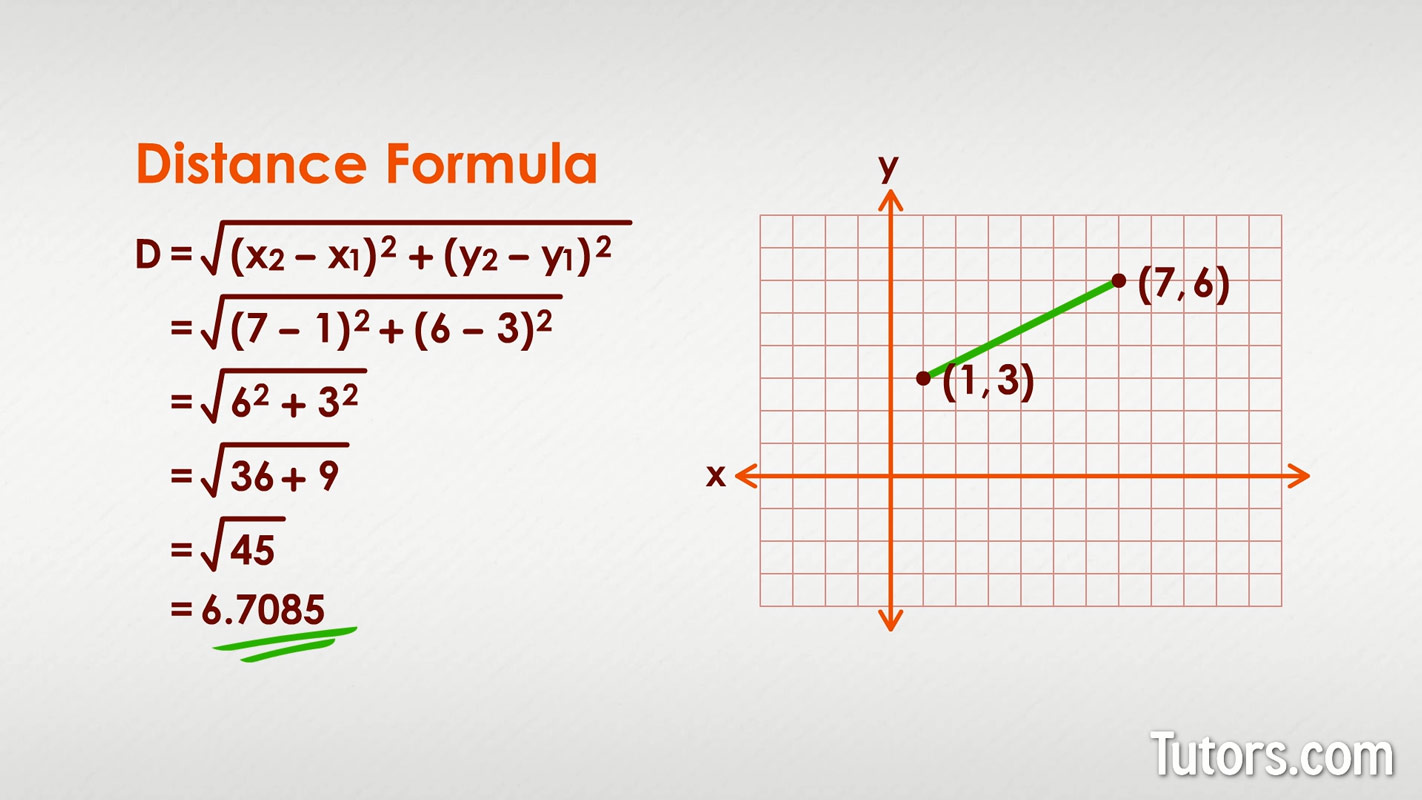
Distance formula examples

You need not even have a coordinate grid in front of you to use the Distance Formula, so long as you have both sets of coordinate points. So, try these three practice problems!

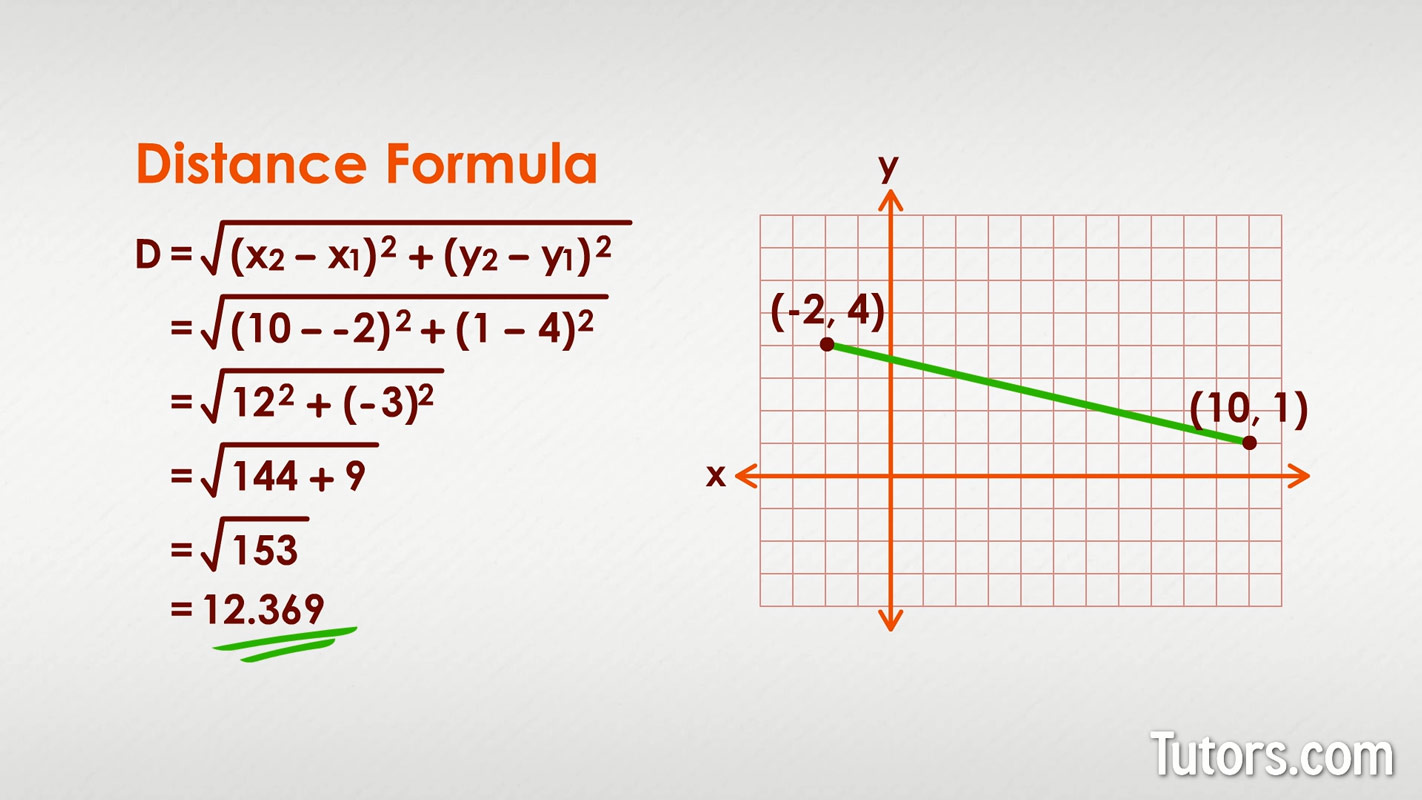
( − 2 , 4 ) (-2, 4) ( − 2 , 4 ) and ( 10 , 1 ) (10, 1) ( 10 , 1 )

( 5 , 5 ) (5, 5) ( 5 , 5 ) and ( 10 , 1 ) (10, 1) ( 10 , 1 )

( − 11 , − 2 ) (-11, -2) ( − 11 , − 2 ) and ( − 21 , − 6 ) (-21, -6) ( − 21 , − 6 )

We will not leave you hanging out on a diagonal. Here are the beginning steps, to help you get started:

D = ( 10 − ( − 2 ) ) 2 + ( 1 − 4 ) 2 D=\sqrt{{(10-(-2))}^{2}+{(1-4)}^{2}} D = ( 10 − ( − 2 )) 2 + ( 1 − 4 ) 2 ​

D = ( 2 − 5 ) 2 + ( 10 − 5 ) 2 D=\sqrt{{(2-5)}^{2}+{(10-5)}^{2}} D = ( 2 − 5 ) 2 + ( 10 − 5 ) 2 ​

D = ( − 21 − ( − 11 ) ) 2 + ( − 6 − ( − 2 ) ) 2 D=\sqrt{{(-21-(-11))}^{2}+{(-6-(-2))}^{2}} D = ( − 21 − ( − 11 )) 2 + ( − 6 − ( − 2 )) 2 ​

What comes next?

D = ( 12 ) 2 + ( − 3 ) 2 D=\sqrt{{\left(12\right)}^{2}+{\left(-3\right)}^{2}} D = ( 12 ) 2 + ( − 3 ) 2 ​

D = ( − 3 ) 2 + ( 5 ) 2 D=\sqrt{{\left(-3\right)}^{2}+{\left(5\right)}^{2}} D = ( − 3 ) 2 + ( 5 ) 2 ​

D = ( − 10 ) 2 + ( − 4 ) 2 D=\sqrt{{\left(-10\right)}^{2}+{\left(-4\right)}^{2}} D = ( − 10 ) 2 + ( − 4 ) 2 ​

You really should be able to take the last few steps by yourself. See if you got these answers:

153 ≈ 12.369 153\approx 12.369 153 ≈ 12.369

34 ≈ 5.8309 34\approx 5.8309 34 ≈ 5.8309

116 ≈ 10.7703 116\approx 10.7703 116 ≈ 10.7703

The distance formula gets its precision and perfection from the concept of using the angled line segment as if it were the hypotenuse of a right triangle formed on the grid.

You need not construct the other two sides to apply the Distance Formula, but you can see those two "sides" in the differences (distances) between x-values (a horizontal line) and y- values (a vertical line).

Lesson summary

Now that you have worked through the lesson and practice, you are able to apply the Distance Formula to the endpoints of any diagonal line segment appearing in a coordinate, or Cartesian, grid. You are also able to relate the Distance Formula to the Pythagorean Theorem.

Pythagoras was a generous and brilliant mathematician, no doubt, but he did not make the great leap to applying the Pythagorean theorem to coordinate grids. To take us from his theorem of the relationships among sides of right triangles to coordinate grids, the mathematical world had to wait for René Descartes.

His Cartesian grid combines geometry and algebra. You can use formulas, including the Distance Formula, to get precise measurements of line segments on the grid.

Exploring the Versatility of the Distance Formula in Mathematics and Physics

Distance formula is an essential mathematical tool used to determine the distance between two points in a Cartesian plane. The Cartesian plane is a coordinate system that comprises two perpendicular axes, the x-axis, and the y-axis.

The intersection of the axes is known as the origin, denoted as (0, 0). Any point in the plane can be represented by a unique ordered pair of coordinates (x, y). The distance formula is derived from the Pythagorean theorem and is used in various fields such as mathematics, physics, and engineering.

The distance formula is given as:

Where d is the distance between two points, (x1, y1) and (x2, y2) are the coordinates of the two points.

The distance formula can be applied to various problems, including finding the distance between two points in a straight line or the distance traveled by an object in motion. In this article, we will explore the distance formula and its applications in various fields.

Deriving the Distance Formula

The distance formula is derived from the Pythagorean theorem , which states that in a right-angled triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side (the hypotenuse). Consider a right-angled triangle with vertices at points A (x1, y1), B (x2, y2), and C (x2, y1), as shown below.

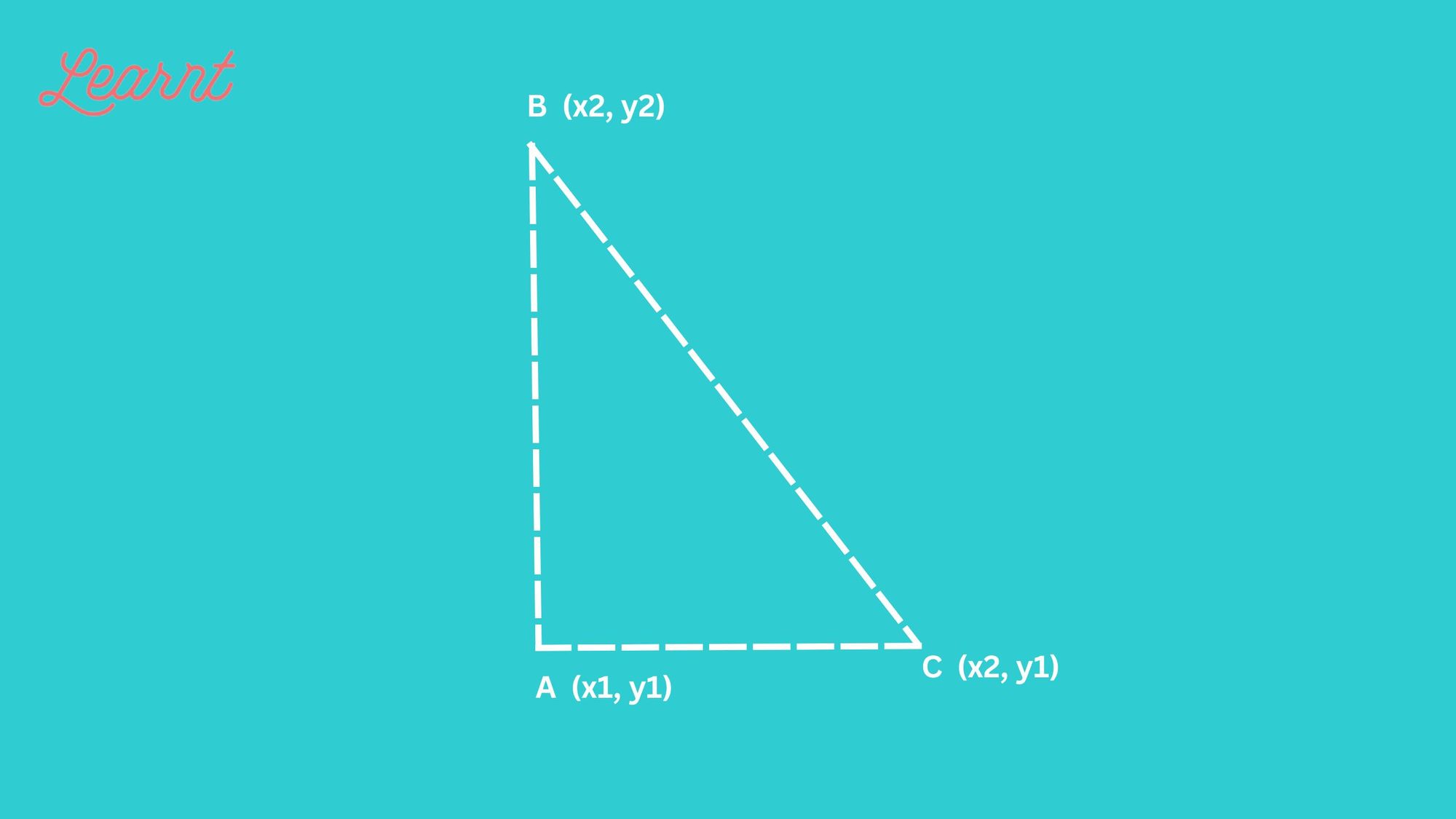
et d1 be the distance between A and C, and d2 be the distance between B and C. We can express d1 and d2 using the Pythagorean theorem as follows:

d1 = √((x2 – x1)² + (y1 – y1)²)

d2 = √((x2 – x2)² + (y2 – y1)²)

Since C is a common point in both triangles, we can express the distance AB as the difference between d1 and d2 as follows:

AB = d1 – d2

Substituting d1 and d2 into the equation, we get:

AB = √((x2 – x1)² + (y1 – y2)²)

Rearranging the equation, we get the distance formula:

d = √((x2 – x1)² + (y2 – y1)²)

Applications of the Distance Formula

The distance formula is a versatile tool that has various applications in different fields. Some of these applications are discussed below.

• Finding the Distance Between Two Points

One of the most common applications of the distance formula is finding the distance between two points in a Cartesian plane . Suppose we have two points A (x1, y1) and B (x2, y2). We can use the distance formula to calculate the distance between these two points as follows:

For example, suppose we have two points A (2, 3) and B (5, 7). We can use the distance formula to find the distance between these two points as follows:

d = √((5 – 2)² + (7 – 3)²)

d = √(3² + 4²)

d = √(9 + 16)

2. Calculating the Distance Traveled by an Object

The distance formula can also be used to calculate the distance traveled by an object in motion. Suppose an object moves from point A (x1, y1) to point B (x2, y2). We can use the distance formula to calculate the distance traveled by the object as follows:

For example, suppose a car moves from point A (2, 3) to point B (5, 7) in a straight line. We can use the distance formula to calculate the distance traveled by the car as follows:

Therefore, the car traveled a distance of 5 units.

3. Calculating the Magnitude of a Vector The distance formula can also be used to calculate the magnitude of a vector. In mathematics , a vector is a quantity that has both magnitude and direction. The magnitude of a vector is its length and is calculated using the distance formula. Suppose we have a vector v with components (a, b). The magnitude of the vector is given as follows:

|v| = √(a² + b²)

For example, suppose we have a vector v with components (3, 4). We can use the distance formula to calculate the magnitude of the vector as follows:

|v| = √(3² + 4²)

|v| = √(9 + 16)

Therefore, the magnitude of the vector v is 5 units.

4.  Finding the Midpoint of a Line Segment

The distance formula can also be used to find the midpoint of a line segment. The midpoint of a line segment is the point that is equidistant from the two endpoints of the segment. Suppose we have a line segment AB with endpoints A (x1, y1) and B (x2, y2). The midpoint of the line segment is given as follows:

((x1 + x2)/2, (y1 + y2)/2)

For example, suppose we have a line segment AB with endpoints A (2, 3) and B (5, 7). We can use the distance formula to find the midpoint of the line segment as follows:

Midpoint = ((2 + 5)/2, (3 + 7)/2)

Midpoint = (3.5, 5)

Therefore, the midpoint of the line segment AB is (3.5, 5).

5.  Calculating the Area of a Triangle

The distance formula can also be used to calculate the area of a triangle. Suppose we have a triangle with vertices at points A (x1, y1), B (x2, y2), and C (x3, y3). The area of the triangle is given as follows:

Area = 0.5 * |(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2))|

For example, suppose we have a triangle with vertices at points A (2, 3), B (5, 7), and C (7, 4). We can use the distance formula to calculate the area of the triangle as follows:

Area = 0.5 * |(2(7 – 4) + 5(4 – 3) + 7(3 – 7))|

Area = 0.5 * |(6 + 5 – 16)|

Area = 0.5 * |-5|

Therefore, the area of the triangle with vertices at points A (2, 3), B (5, 7), and C (7, 4) is 2.5 square units.

In conclusion, the distance formula is an important tool in mathematics and physics . It allows us to calculate the distance between two points in a coordinate plane and is used in various applications such as finding the distance traveled by an object, calculating the magnitude of a vector, finding the midpoint of a line segment, and calculating the area of a triangle.

The formula is simple to use and can be applied to solve a wide range of problems. By understanding and mastering the distance formula, students can improve their problem-solving skills and develop a deeper understanding of mathematics and physics concepts.

What Is Math Is Fun?

Exploring the World of Cool Math Games

10 Reasons to Start Using Math Games to Learn

Fun and Educational Math Games for Kids

Subscribe to new posts.