what is hypothesis error

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10, introduction to type i and type ii errors.

• Examples identifying Type I and Type II errors
• Type I vs Type II error
• Introduction to power in significance tests
• Examples thinking about power in significance tests
• Error probabilities and power
• Consequences of errors and significance

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.1 - type i and type ii errors.

When conducting a hypothesis test there are two possible decisions: reject the null hypothesis or fail to reject the null hypothesis. You should remember though, hypothesis testing uses data from a sample to make an inference about a population. When conducting a hypothesis test we do not know the population parameters. In most cases, we don't know if our inference is correct or incorrect.

When we reject the null hypothesis there are two possibilities. There could really be a difference in the population, in which case we made a correct decision. Or, it is possible that there is not a difference in the population (i.e., \(H_0\) is true) but our sample was different from the hypothesized value due to random sampling variation. In that case we made an error. This is known as a Type I error.

When we fail to reject the null hypothesis there are also two possibilities. If the null hypothesis is really true, and there is not a difference in the population, then we made the correct decision. If there is a difference in the population, and we failed to reject it, then we made a Type II error.

Rejecting \(H_0\) when \(H_0\) is really true, denoted by \(\alpha\) ("alpha") and commonly set at .05

     \(\alpha=P(Type\;I\;error)\)

Failing to reject \(H_0\) when \(H_0\) is really false, denoted by \(\beta\) ("beta")

     \(\beta=P(Type\;II\;error)\)

Example: Trial Section  

A man goes to trial where he is being tried for the murder of his wife.

We can put it in a hypothesis testing framework. The hypotheses being tested are:

• \(H_0\) : Not Guilty
• \(H_a\) : Guilty

Type I error  is committed if we reject \(H_0\) when it is true. In other words, did not kill his wife but was found guilty and is punished for a crime he did not really commit.

Type II error  is committed if we fail to reject \(H_0\) when it is false. In other words, if the man did kill his wife but was found not guilty and was not punished.

Example: Culinary Arts Study Section  

A group of culinary arts students is comparing two methods for preparing asparagus: traditional steaming and a new frying method. They want to know if patrons of their school restaurant prefer their new frying method over the traditional steaming method. A sample of patrons are given asparagus prepared using each method and asked to select their preference. A statistical analysis is performed to determine if more than 50% of participants prefer the new frying method:

• \(H_{0}: p = .50\)
• \(H_{a}: p>.50\)

Type I error  occurs if they reject the null hypothesis and conclude that their new frying method is preferred when in reality is it not. This may occur if, by random sampling error, they happen to get a sample that prefers the new frying method more than the overall population does. If this does occur, the consequence is that the students will have an incorrect belief that their new method of frying asparagus is superior to the traditional method of steaming.

Type II error  occurs if they fail to reject the null hypothesis and conclude that their new method is not superior when in reality it is. If this does occur, the consequence is that the students will have an incorrect belief that their new method is not superior to the traditional method when in reality it is.

Type 1 and Type 2 Errors in Statistics

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

On This Page:

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty). Because a p -value is based on probabilities, there is always a chance of making an incorrect conclusion regarding accepting or rejecting the null hypothesis ( H 0 ).

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

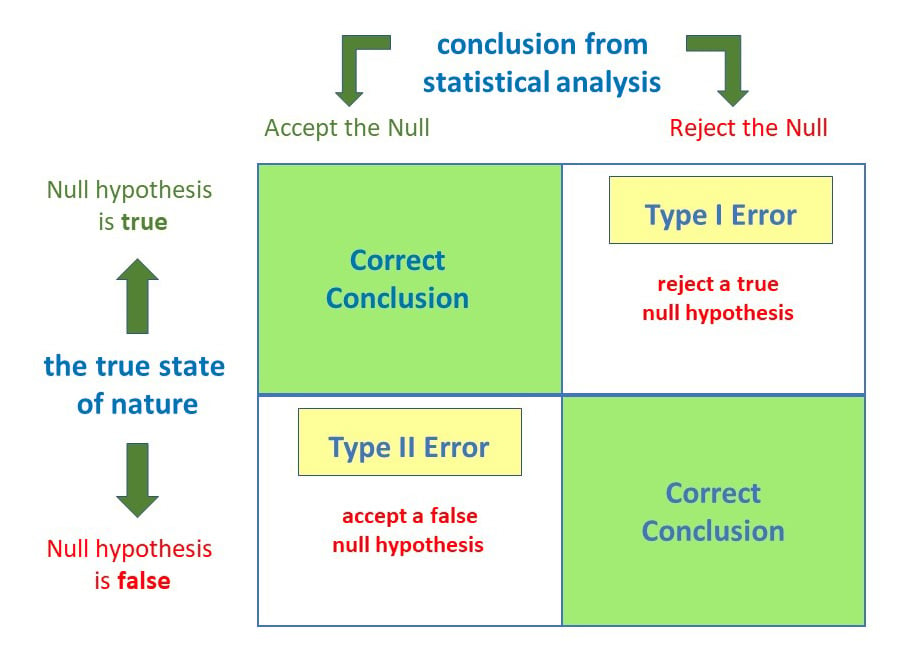
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis , increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

Type I error 

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p- value below which you reject the null hypothesis.

A p -value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

• Null Hypothesis (H0) : MediCure is no more effective at reducing fever than the placebo.
• Alternative Hypothesis (H1) : MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error : The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

Resource Allocation : Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

Unnecessary Interventions : In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

Reputation and Credibility : For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

Type II error

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

• Null Hypothesis (H0) : The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
• Alternative Hypothesis (H1) : The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error : By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Missed Opportunities : A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

Potential Risks : In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

Stagnation : In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.

How do Type I and Type II errors relate to psychological research and experiments?

Type I errors are like false alarms, while Type II errors are like missed opportunities. Both errors can impact the validity and reliability of psychological findings, so researchers strive to minimize them to draw accurate conclusions from their studies.

How does sample size influence the likelihood of Type I and Type II errors in psychological research?

Sample size in psychological research influences the likelihood of Type I and Type II errors. A larger sample size reduces the chances of Type I errors, which means researchers are less likely to mistakenly find a significant effect when there isn’t one.

A larger sample size also increases the chances of detecting true effects, reducing the likelihood of Type II errors.

Are there any ethical implications associated with Type I and Type II errors in psychological research?

Yes, there are ethical implications associated with Type I and Type II errors in psychological research.

Type I errors may lead to false positive findings, resulting in misleading conclusions and potentially wasting resources on ineffective interventions. This can harm individuals who are falsely diagnosed or receive unnecessary treatments.

Type II errors, on the other hand, may result in missed opportunities to identify important effects or relationships, leading to a lack of appropriate interventions or support. This can also have negative consequences for individuals who genuinely require assistance.

Therefore, minimizing these errors is crucial for ethical research and ensuring the well-being of participants.

Further Information

• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Related Articles

Exploratory Data Analysis

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research

Hypothesis Testing and Types of Errors

Article info.

• Statistical Inference
• Null Hypothesis
• Bayes Factor
• Bayesian Inference
• Sampling and Estimation

Article Versions

• 14 2021-05-28 15:47:23 2562,2561 14,2562 By arvindpdmn Adding info on base rate and confidence interval.
• 13 2021-05-28 15:20:55 2561,2560 13,2561 By arvindpdmn Minor edit
• 12 2021-05-28 15:11:35 2560,2559 12,2560 By arvindpdmn Milestones added. Added question on misconceptions.
• 11 2021-05-28 13:22:05 2559,2116 11,2559 By arvindpdmn Minor reordering of questions. Merge two questions into one. Added more refs and citations to remove warnings. Other corrections. Milestones are pending.
• 10 2020-07-15 06:11:06 2116,1611 10,2116 By arvindpdmn Reducing to 8 tags. This is the maximum that will be imposed in the next release. Corrected spelling.
• Submitting ... You are editing an existing chat message. All Versions 2021-05-28 15:47:23 by arvindpdmn 2021-05-28 15:20:55 by arvindpdmn 2021-05-28 15:11:35 by arvindpdmn 2021-05-28 13:22:05 by arvindpdmn 2020-07-15 06:11:06 by arvindpdmn 2019-09-23 10:56:34 by arvindpdmn 2019-03-13 15:34:32 by arvindpdmn 2018-05-29 05:32:41 by arvindpdmn 2018-05-27 12:14:19 by raam.raam 2018-05-26 11:37:25 by raam.raam 2018-05-21 10:59:24 by arvindpdmn 2018-05-21 10:46:31 by arvindpdmn 2018-05-18 07:27:06 by raam.raam 2018-05-18 06:19:18 by raam.raam All Sections Summary Discussion Sample Code References Milestones Tags See Also Further Reading
• 2021-05-28 13:12:19 - By raam.raam It is the error rate that is related and not error quantum. The following article puts this nicely. https://www.scribbr.com/statistics/type-i-and-type-ii-errors/#:~:text=Trade%2Doff%20between%20Type%20I%20and%20Type%20II%20errors,-The%20Type%20I&text=This%20means%20there's%20an%20important,a%20Type%20I%20error%20risk.
• 2021-05-28 12:57:18 - By arvindpdmn I am anyway updating the article to remove warnings. Will edit as part of the update.
• 2021-05-28 12:36:34 - 1 By raam.raam I will correct the relationship between alpha and beta. They are dependent
• 2021-05-28 12:05:26 - By raam.raam as a special case when null and alternate hypotheses distributions are overlapping, it may be. But don't think can be generalized. I will look for more references.
• 2021-05-28 11:30:47 - 1 By arvindpdmn Need to clarify "Errors α and β are independent of each other. Increasing one does not decrease the other.". This ref says otherwise: https://www.afit.edu/stat/statcoe_files/8__The_Logic_of_Statistical_Hypothesis_Testing.pdf

Suppose we want to study income of a population. We study a sample from the population and draw conclusions. The sample should represent the population for our study to be a reliable one.

Null hypothesis \((H_0)\) is that sample represents population. Hypothesis testing provides us with framework to conclude if we have sufficient evidence to either accept or reject null hypothesis.

Population characteristics are either assumed or drawn from third-party sources or judgements by subject matter experts. Population data and sample data are characterised by moments of its distribution (mean, variance, skewness and kurtosis). We test null hypothesis for equality of moments where population characteristic is available and conclude if sample represents population.

For example, given only mean income of population, we validate if mean income of sample is close to population mean to conclude if sample represents the population.

Population mean and population variance are denoted in Greek alphabets \(\mu\) and \(\sigma^2\) respectively, while sample mean and sample variance are denoted in English alphabets \(\bar x\) and \(s^2\) respectively.

• If the difference is not significant, we conclude the difference is due to sampling. This is called sampling error and this happens due to chance.
• If the difference is significant, we conclude the sample does not represent the population. The reason has to be more than chance for difference to be explained.

Hypothesis testing helps us to conclude if the difference is due to sampling error or due to reasons beyond sampling error.

A common assumption is that the observations are independent and come from a random sample. The population distribution must be Normal or the sample size is large enough. If the sample size is large enough, we can invoke the Central Limit Theorem ( CLT ) regardless of the underlying population distribution. Due to CLT , sampling distribution of the sample statistic (such as sample mean) will be approximately a Normal distribution.

A rule of thumb is 30 observations but in some cases even 10 observations may be sufficient to invoke the CLT . Others require at least 50 observations.

When acceptance of \(H_0\) involves boundaries on both sides, we invoke the two-tailed test . For example, if we define \(H_0\) as sample drawn from population with age limits in the range of 25 to 35, then testing of \(H_0\) involves limits on both sides.

Suppose we define the population as greater than age 50, we are interested in rejecting a sample if the age is less than or equal to 50; we are not concerned about any upper limit. Here we invoke the one-tailed test . A one-tailed test could be left-tailed or right-tailed.

• \(H_0\): \(\mu = \$ 2.62\)
• \(H_1\) right-tailed: \(\mu > \$ 2.62\)
• \(H_1\) two-tailed: \(\mu \neq \$ 2.62\)

• Not accepting that sample represents population when in reality it does. This is called type-I or \(\alpha\) error .
• Accepting that sample represents population when in reality it does not. This is called type-II or \(\beta\) error .

For instance, granting loan to an applicant with low credit score is \(\alpha\) error. Not granting loan to an applicant with high credit score is (\(\beta\)) error.

The symbols \(\alpha\) and \(\beta\) are used to represent the probability of type-I and type-II errors respectively.

The p-value can be interpreted as the probability of getting a result that's same or more extreme when the null hypothesis is true.

The observed sample mean \(\bar x\) is overlaid on population distribution of values with mean \(\mu\) and variance \(\sigma^2\). The proportion of values beyond \(\bar x\) and away from \(\mu\) (either in left tail or in right tail or in both tails) is p-value . If p-value <= \(\alpha\) we reject null hypothesis. The results are said to be statistically significant and not due to chance.

Assuming \(\alpha\)=0.05, p-value > 5%, we conclude the sample is highly likely to be drawn from population with mean \(\mu\) and variance \(\sigma^2\). We accept \((H_0)\). Otherwise, there's insufficient evidence to be part of population and we reject \(H_0\).

We preselect \(\alpha\) based on how much type-I error we're willing to tolerate. \(\alpha\) is called level of significance . The standard for level of significance is 0.05 but in some studies it may be 0.01 or 0.1. In the case of two-tailed tests, it's \(\alpha/2\) on either side.

Law of Large Numbers suggests larger the sample size, the more accurate the estimate. Accuracy means the variance of estimate will tend towards zero as sample size increases. Sample Size can be determined to suit accepted level of tolerance for deviation.

Confidence interval of sample mean is determined from sample mean offset by variance on either side of the sample mean. If the population variance is known, then we conduct z-test based on Normal distribution. Otherwise, variance has to be estimated and we use t-test based on t-distribution.

The formulae for determining sample size and confidence interval depends on what we to estimate (mean/variance/others), sampling distribution of estimate and standard deviation of estimate's sampling distribution.

We overlay sample mean's distribution on population distribution, the proportion of overlap of sampling estimate's distribution on population distribution is \(\beta\) error .

Larger the overlap, larger the chance the sample does belong to population with mean \(\mu\) and variance \(\sigma^2\). Incidentally, despite the overlap, p-value may be less than 5%. This happens when sample mean is way off population mean, but the variance of sample mean is such that the overlap is significant.

Errors \(\alpha\) and \(\beta\) are dependent on each other. Increasing one decreases the other. Choosing suitable values for these depends on the cost of making these errors. Perhaps it's worse to convict an innocent person (type-I error) than to acquit a guilty person (type-II error), in which case we choose a lower \(\alpha\). But it's possible to decrease both errors but collecting more data.

• Probability of rejecting the null hypothesis when, in fact, it is false.
• Probability that a test of significance will pick up on an effect that is present.
• Probability of avoiding a Type II error.

Low p-value and high power help us decisively conclude sample doesn't belong to population. When we cannot conclude decisively, it's advisable to go for larger samples and multiple samples.

In fact, power is increased by increasing sample size, effect sizes and significance levels. Variance also affects power.

A common misconception is to consider "p value as the probability that the null hypothesis is true". In fact, p-value is computed under the assumption that the null hypothesis is true. P-value is the probability of observing the values, or more extremes values, if the null hypothesis is true.

Another misconception, sometimes called base rate fallacy , is that under controlled \(\alpha\) and adequate power, statistically significant results correspond to true differences. This is not the case, as shown in the figure. Even with \(\alpha\)=5% and power=80%, 36% of statistically significant p-values will not report the true difference. This is because only 10% of the null hypotheses are false (base rate) and 80% power on these gives only 80 true positives.

P-value doesn't measure the size of the effect, for which confidence interval is a better approach. A drug that gives 25% improvement may not mean much if symptoms are innocuous compared to another drug that gives small improvement from a disease that leads to certain death. Context is therefore important.

The field of statistical testing probably starts with John Arbuthnot who applies it to test sex ratios at birth. Subsequently, others in the 18th and 19th centuries use it in other fields. However, modern terminology (null hypothesis, p-value, type-I or type-II errors) is formed only in the 20th century.

Pearson introduces the concept of p-value with the chi-squared test. He gives equations for calculating P and states that it's "the measure of the probability of a complex system of n errors occurring with a frequency as great or greater than that of the observed system."

Ronald A. Fisher develops the concept of p-value and shows how to calculate it in a wide variety of situations. He also notes that a value of 0.05 may be considered as conventional cut-off.

Neyman and Pearson publish On the problem of the most efficient tests of statistical hypotheses . They introduce the notion of alternative hypotheses . They also describe both type-I and type-II errors (although they don't use these terms). They state, "Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behaviour with regard to them, in following which we insure that, in the long run of experience, we shall not be too often wrong."

Johnson's textbook titled Statistical methods in research is perhaps the first to introduce to students the Neyman-Pearson hypothesis testing at a time when most textbooks follow Fisher's significance testing. Johnson uses the terms "error of the first kind" and "error of the second kind". In time, Fisher's approach is called P-value approach and the Neyman-Pearson approach is called fixed-α approach .

Carver makes the following suggestions: use of the term "statistically significant"; interpret results with respect to the data first and statistical significance second; and pay attention to the size of the effect.

• Biau, David Jean, Brigitte M. Jolles, and Raphaël Porcher. 2010. "P Value and the Theory of Hypothesis Testing: An Explanation for New Researchers." Clin Orthop Relat Res, vol. 468, no. 3, pp. 885–892, March. Accessed 2021-05-28.
• Carver, Ronald P. 1993. "The Case against Statistical Significance Testing, Revisited." The Journal of Experimental Education, vol. 61, no. 4, Statistical Significance Testing in Contemporary Practice, pp. 287-292. Accessed 2021-05-28.
• Frankfort-Nachmias, Chava, Anna Leon-Guerrero, and Georgiann Davis. 2020. "Chapter 8: Testing Hypotheses." In: Social Statistics for a Diverse Society, SAGE Publications. Accessed 2021-05-28.
• Gordon, Max. 2011. "How to best display graphically type II (beta) error, power and sample size?" August 11. Accessed 2018-05-18.
• Heard, Stephen B. 2015. "In defence of the P-value" Types of Errors. February 9. Updated 2015-12-04. Accessed 2018-05-18.
• Huberty, Carl J. 1993. "Historical Origins of Statistical Testing Practices: The Treatment of Fisher versus Neyman-Pearson Views in Textbooks." The Journal of Experimental Education, vol. 61, no. 4, Statistical Significance Testing in Contemporary Practice, pp. 317-333. Accessed 2021-05-28.
• Kensler, Jennifer. 2013. "The Logic of Statistical Hypothesis Testing: Best Practice." Report, STAT T&E Center of Excellence. Accessed 2021-05-28.
• Klappa, Peter. 2014. "Sampling error and hypothesis testing." On YouTube, December 10. Accessed 2021-05-28.
• Lane, David M. 2021. "Section 10.8: Confidence Interval on the Mean." In: Introduction to Statistics, Rice University. Accessed 2021-05-28.
• McNeese, Bill. 2015. "How Many Samples Do I Need?" SPC For Excel, BPI Consulting, June. Accessed 2018-05-18.
• McNeese, Bill. 2017. "Interpretation of Alpha and p-Value." SPC for Excel, BPI Consulting, April 6. Updated 2020-04-25. Accessed 2021-05-28.
• Neyman, J., and E. S. Pearson. 1933. "On the problem of the most efficient tests of statistical hypotheses." Philos Trans R Soc Lond A., vol. 231, issue 694-706, pp. 289–337. doi: 10.1098/rsta.1933.0009. Accessed 2021-05-28.
• Nurse Key. 2017. "Chapter 15: Sampling." February 17. Accessed 2018-05-18.
• Pearson, Karl. 1900. "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling." Philosophical Magazine, Series 5 (1876-1900), pp. 157–175. Accessed 2021-05-28.
• Reinhart, Alex. 2015. "Statistics Done Wrong: The Woefully Complete Guide." No Starch Press.
• Rolke, Wolfgang A. 2018. "Quantitative Variables." Department of Mathematical Sciences, University of Puerto Rico - Mayaguez. Accessed 2018-05-18.
• Six-Sigma-Material.com. 2016. "Population & Samples." Six-Sigma-Material.com. Accessed 2018-05-18.
• Walmsley, Angela and Michael C. Brown. 2017. "What is Power?" Statistics Teacher, American Statistical Association, September 15. Accessed 2021-05-28.
• Wang, Jing. 2014. "Chapter 4.II: Hypothesis Testing." Applied Statistical Methods II, Univ. of Illinois Chicago. Accessed 2021-05-28.
• Weigle, David C. 1994. "Historical Origins of Contemporary Statistical Testing Practices: How in the World Did Significance Testing Assume Its Current Place in Contemporary Analytic Practice?" Paper presented at the Annual Meeting of the Southwest Educational Research Association, SanAntonio, TX, January 27. Accessed 2021-05-28.
• Wikipedia. 2018. "Margin of Error." May 1. Accessed 2018-05-18.
• Wikipedia. 2021. "Law of large numbers." Wikipedia, March 26. Accessed 2021-05-28.
• howMed. 2013. "Significance Testing and p value." August 4. Updated 2013-08-08. Accessed 2018-05-18.

Further Reading

• Foley, Hugh. 2018. "Introduction to Hypothesis Testing." Skidmore College. Accessed 2018-05-18.
• Buskirk, Trent. 2015. "Sampling Error in Surveys." Accessed 2018-05-18.
• Zaiontz, Charles. 2014. "Assumptions for Statistical Tests." Real Statistics Using Excel. Accessed 2018-05-18.
• DeCook, Rhonda. 2018. "Section 9.2: Types of Errors in Hypothesis testing." Stat1010 Notes, Department of Statistics and Actuarial Science, University of Iowa. Accessed 2018-05-18.

Article Stats

Author-wise stats for article edits.

• Browse Articles
• Community Outreach
• About Devopedia
• Author Guidelines
• FAQ & Help
• Forgot your password?
• Create an account

• Search Search Please fill out this field.

What Is a Type II Error?

• How It Works
• Type I vs. Type II Error

The Bottom Line

• Corporate Finance
• Financial Analysis

Type II Error Explained, Plus Example & vs. Type I Error

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Michela Buttignol / Investopedia

A type II error is a statistical term used within the context of hypothesis testing that describes the error that occurs when one fails to reject a null hypothesis that is actually false. A type II error produces a false negative, also known as an error of omission.

For example, a test for a disease may report a negative result when the patient is infected. This is a type II error because we accept the conclusion of the test as negative, even though it is incorrect.

A type II error can be contrasted with a type I error in that the latter is the rejection of a true null hypothesis, whereas the former describes the error that occurs when one fails to reject a null hypothesis that is actually false. A type II error rejects the alternative hypothesis, even though it does not occur due to chance.

Key Takeaways

• A type II error is defined as the probability of incorrectly failing to reject the null hypothesis, when in fact it is not applicable to the entire population.
• A type II error is essentially a false negative.
• A type II error can be reduced by making more stringent criteria for rejecting a null hypothesis, although this increases the chances of a false positive.
• The sample size, the true population size, and the preset alpha level influence the magnitude of risk of an error.
• Analysts need to weigh the likelihood and impact of type II errors with type I errors.

Understanding a Type II Error

A type II error, also known as an error of the second kind or a beta error, confirms an idea that should have been rejected—for instance, claiming that two observances are the same, despite them being different. A type II error does not reject the null hypothesis, even though the alternative hypothesis is the true state of nature. In other words, a false finding is accepted as true.

A type II error can be reduced by making more stringent criteria for rejecting a null hypothesis (H 0 ). For example, if an analyst is considering anything that falls within the +/- bounds of a 95% confidence interval as statistically insignificant (a negative result), then by decreasing that tolerance to +/- 90%, and subsequently narrowing the bounds, you will get fewer negative results, and thus reduce the chances of a false negative.

Taking these steps, however, tends to increase the chances of encountering a type I error—a false-positive result. When conducting a hypothesis test, the probability or risk of making a type I error or type II error should be considered.

The steps taken to reduce the chances of encountering a type II error tend to increase the probability of a type I error.

Type I Errors vs. Type II Errors

The difference between a type II error and a type I error is that a type I error rejects the null hypothesis when it is true (i.e., a false positive). The probability of committing a type I error is equal to the level of significance that was set for the hypothesis test. Therefore, if the level of significance is 0.05, there is a 5% chance that a type I error may occur.

The probability of committing a type II error is equal to one minus the power of the test, also known as beta. The power of the test could be increased by increasing the sample size, which decreases the risk of committing a type II error.

Some statistical literature will include overall significance level and type II error risk as part of the report’s analysis. For example, a 2021 meta-analysis of exosome in the treatment of spinal cord injury recorded an overall significance level of 0.05 and a type II error risk of 0.1.

Example of a Type II Error

Assume a biotechnology company wants to compare how effective two of its drugs are for treating diabetes. The null hypothesis states the two medications are equally effective. A null hypothesis, H 0 , is the claim that the company hopes to reject using the one-tailed test . The alternative hypothesis, H a , states that the two drugs are not equally effective. The alternative hypothesis, H a , is the state of nature that is supported by rejecting the null hypothesis.

The biotech company implements a large clinical trial of 3,000 patients with diabetes to compare the treatments. The company randomly divides the 3,000 patients into two equally sized groups, giving one group one of the treatments and the other group the other treatment. It selects a significance level of 0.05, which indicates it is willing to accept a 5% chance it may reject the null hypothesis when it is true or a 5% chance of committing a type I error.

Assume the beta is calculated to be 0.025, or 2.5%. Therefore, the probability of committing a type II error is 97.5%. If the two medications are not equal, the null hypothesis should be rejected. However, if the biotech company does not reject the null hypothesis when the drugs are not equally effective, then a type II error occurs.

What Is the Difference Between Type I and Type II Errors?

A type I error occurs if a null hypothesis is rejected that is actually true in the population. This type of error is representative of a false positive. Alternatively, a type II error occurs if a null hypothesis is not rejected that is actually false in the population. This type of error is representative of a false negative.

What Causes Type II Errors?

A type II error is commonly caused if the statistical power of a test is too low. The higher the statistical power, the greater the chance of avoiding an error. It’s often recommended that the statistical power should be set to at least 80% prior to conducting any testing.

What Factors Influence the Magnitude of Risk for Type II Errors?

As the sample size of the research increases, the magnitude of risk for type II errors should decrease. As the true population effect size increases, the type II error should also decrease. Finally, the preset alpha level set by the research influences the magnitude of risk. As the alpha level set decreases, the risk of a type II error increases.

How Can a Type II Error Be Minimized?

It is not possible to fully prevent committing a type II error, but the risk can be minimized by increasing the sample size. However, doing so will also increase the risk of committing a type I error instead.

In statistics, a type II error results in a false negative—meaning that there is a finding, but it has been missed in the analysis (or that the null hypothesis is not rejected when it ought to have been). A type II error can occur if there is not enough power in statistical tests, often resulting from sample sizes that are too small. Increasing the sample size can help reduce the chances of committing a type II error.

Type II errors can be contrasted with type I errors, which are false positives.

Europe PMC. “ A Meta-Analysis of Exosome in the Treatment of Spinal Cord Injury .”

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Key Differences

Know the Differences & Comparisons

Difference Between Type I and Type II Errors

The testing of hypothesis is a common procedure; that researcher use to prove the validity, that determines whether a specific hypothesis is correct or not. The result of testing is a cornerstone for accepting or rejecting the null hypothesis (H 0 ). The null hypothesis is a proposition; that does not expect any difference or effect. An alternative hypothesis (H 1 ) is a premise that expects some difference or effect.

There are slight and subtle differences between type I and type II errors, that we are going to discuss in this article.

Content: Type I Error Vs Type II Error

Comparison chart, possible outcomes, definition of type i error.

In statistics, type I error is defined as an error that occurs when the sample results cause the rejection of the null hypothesis, in spite of the fact that it is true. In simple terms, the error of agreeing to the alternative hypothesis, when the results can be ascribed to chance.

Also known as the alpha error, it leads the researcher to infer that there is a variation between two observances when they are identical. The likelihood of type I error, is equal to the level of significance, that the researcher sets for his test. Here the level of significance refers to the chances of making type I error.

E.g. Suppose on the basis of data, the research team of a firm concluded that more than 50% of the total customers like the new service started by the company, which is, in fact, less than 50%.

Definition of Type II Error

When on the basis of data, the null hypothesis is accepted, when it is actually false, then this kind of error is known as Type II Error. It arises when the researcher fails to deny the false null hypothesis. It is denoted by Greek letter ‘beta (β)’ and often known as beta error.

Type II error is the failure of the researcher in agreeing to an alternative hypothesis, although it is true. It validates a proposition; that ought to be refused. The researcher concludes that the two observances are identical when in fact they are not.

The likelihood of making such error is analogous to the power of the test. Here, the power of test alludes to the probability of rejecting of the null hypothesis, which is false and needs to be rejected. As the sample size increases, the power of test also increases, that results in the reduction in risk of making type II error.

E.g. Suppose on the basis of sample results, the research team of an organisation claims that less than 50% of the total customers like the new service started by the company, which is, in fact, greater than 50%.

Key Differences Between Type I and Type II Error

The points given below are substantial so far as the differences between type I and type II error is concerned:

• Type I error is an error that takes place when the outcome is a rejection of null hypothesis which is, in fact, true. Type II error occurs when the sample results in the acceptance of null hypothesis, which is actually false.
• Type I error or otherwise known as false positives, in essence, the positive result is equivalent to the refusal of the null hypothesis. In contrast, Type II error is also known as false negatives, i.e. negative result, leads to the acceptance of the null hypothesis.
• When the null hypothesis is true but mistakenly rejected, it is type I error. As against this, when the null hypothesis is false but erroneously accepted, it is type II error.
• Type I error tends to assert something that is not really present, i.e. it is a false hit. On the contrary, type II error fails in identifying something, that is present, i.e. it is a miss.
• The probability of committing type I error is the sample as the level of significance. Conversely, the likelihood of committing type II error is same as the power of the test.
• Greek letter ‘α’ indicates type I error. Unlike, type II error which is denoted by Greek letter ‘β’.

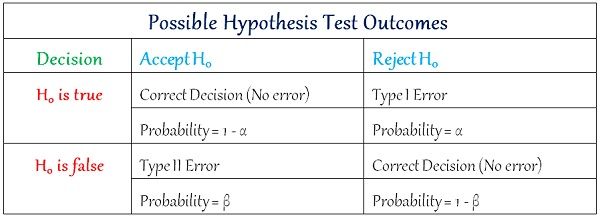
By and large, Type I error crops up when the researcher notice some difference, when in fact, there is none, whereas type II error arises when the researcher does not discover any difference when in truth there is one. The occurrence of the two kinds of errors is very common as they are a part of testing process. These two errors cannot be removed completely but can be reduced to a certain level.

You Might Also Like:

Sajib banik says

January 19, 2017 at 11:00 pm

useful information

Tomisi says

May 10, 2018 at 11:48 pm

Thanks, the simplicity of your illusrations in essay and tables is great contribution to the demystification of statistics.

Tika Ram Khatiwada says

January 9, 2019 at 1:39 pm

Very simply and clearly defined.

sanjaya says

January 9, 2019 at 3:56 pm

Good article..

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.7: The Two Errors in Null Hypothesis Significance Testing

• Last updated
• Save as PDF
• Page ID 17354

• Michelle Oja
• Taft College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Before going into details about how a statistical test is constructed, it’s useful to understand the philosophy behind it. We hinted at it when pointing out the similarity between a null hypothesis test and a criminal trial, but let's be explicit.

Ideally, we would like to construct our test so that we never make any errors. Unfortunately, since the world is messy, this is never possible . Sometimes you’re just really unlucky: for instance, suppose you flip a coin 10 times in a row and it comes up heads all 10 times. That feels like very strong evidence that the coin is biased, but of course there’s a 1 in 1024 chance that this would happen even if the coin was totally fair. In other words, in real life we always have to accept that there’s a chance that we made the wrong statistical decision. The goal behind statistical hypothesis testing is not to eliminate errors, because that's impossible, but to minimize them.

At this point, we need to be a bit more precise about what we mean by “errors”. Firstly, let’s state the obvious: it is either the case that the null hypothesis is true, or it is false.  The means are either similar or they ar not.  The sample is either from the population, or it is not.  Our test will either reject the null hypothesis or retain it.  So, as the Table \(\PageIndex{1}\) illustrates, after we run the test and make our choice, one of four things might have happened:

As a consequence there are actually two different types of error here. If we reject a null hypothesis that is actually true, then we have made a type I error . On the other hand, if we retain the null hypothesis when it is in fact false, then we have made a type II error .  Note that this does not mean that you, as the statistician, made a mistake.  It means that, even when all evidence supports a conclusion, just by chance, you might have a wonky sample that shows you something that isn't true.

Errors in Null Hypothesis Significance Testing

Type i error.

• The sample is from the population, but we say that it’s not (rejecting the null).
• Saying there is a mean difference when there really isn’t one!
• alpha (α, a weird a)
• False positive

Type II Error

• The sample is from a different population, but we say that the means are similar (retaining the null).
• Saying there is not a mean difference when there really is one!
• beta (β, a weird B)
• Missed effect

Why the Two Types of Errors Matter

Null Hypothesis Significance Testing (NHST) is based on the idea that large mean differences would be rare if the sample was from the population.  So, if the sample mean is different enough (greater than the critical value) then the effect would be rare enough (< .05) to reject the null hypothesis and conclude that the means are different (the sample is not from the population).  However, about 5% of the times when we reject the null hypothesis, saying that the sample is from a different population, because we are wrong .  Null Hypothesis Significance Testing is not a “sure thing.”  Instead, we have a known error rate (5%). Because of this, replication is emphasized to further support research hypotheses.  For research and statistics, “replication” means that we do many experiments to test the same idea.  We do this in the hopes that we might get a wonky sample 5% of the time, but if we do enough experiments we will recognize the wonky 5%.

Remember how statistical testing was kind of like a criminal trial? Well,a criminal trial requires that you establish “beyond a reasonable doubt” that the defendant did it. All of the evidentiary rules are (in theory, at least) designed to ensure that there’s (almost) no chance of wrongfully convicting an innocent defendant. The trial is designed to protect the rights of a defendant: as the English jurist William Blackstone famously said, it is “better that ten guilty persons escape than that one innocent suffer.” In other words, a criminal trial doesn’t treat the two types of error in the same way:  punishing the innocent is deemed to be much worse than letting the guilty go free. A statistical test is pretty much the same: the single most important design principle of the test is to control the probability of a type I error, to keep it below some fixed probability (we use 5%). This probability, which is denoted α, is called the significance level of the test (or sometimes, the size of the test). 

Introduction to Power

So, what about the type II error rate? Well, we’d also like to keep those under control too, and we denote this probability by β (beta). However, it’s much more common to refer to the power of the test, which is the probability with which we reject a null hypothesis when it really is false, which is 1−β. To help keep this straight, here’s the same table again, but with the relevant numbers added:

“powerful” hypothesis test is one that has a small value of β, while still keeping α fixed at some (small) desired level. By convention, scientists usually use 5% (p = .05, α levels of .05) as the marker for Type I errors (although we also use of lower α levels of 01 and .001 when we find something that appears to be really rare). The tests are designed to ensure that the α level is kept small (accidently rejecting a null hypothesis when it is true), but there’s no corresponding guarantee regarding β (accidently retaining the null hypothesis when the null hypothesis is actually false). We’d certainly like the type II error rate to be small, and we try to design tests that keep it small, but this is very much secondary to the overwhelming need to control the type I error rate. As Blackstone might have said if he were a statistician, it is “better to retain 10 false null hypotheses than to reject a single true one”.  To add complication, some researchers don't agree with this philosophy, believing that there are situations where it makes sense, and situations where I think it doesn’t.  But that’s neither here nor there. It’s how the tests are built.

Can we decrease the chance of Type I Error and decrease the chance of Type II Error?  Can we make fewer false positives and miss fewer real differences?

Unfortunately, no.  If we want fewer false positive, then we will miss more real effects.  What we can do is increase the power of finding any real differences.  We'll talk a little more about Power in terms of statistical analyses next.  

Contributors and Attributions

• Danielle Navarro  ( University of New South Wales )

Dr. MO ( Taft College )

Help | Advanced Search

Mathematics > Number Theory

Title: values of random polynomials under the riemann hypothesis.

Abstract: The well-known result states that the square-free counting function up to $N$ is $N/\zeta(2)+O(N^{1/2})$. This corresponds to the identity polynomial $\text{Id}(x)$. It is expected that the error term in question is $O_\varepsilon(N^{\frac{1}{4}+\varepsilon})$ for arbitraliy small $\varepsilon>0$. Usually, it is more difficult to obtain similar order of error term for a higher degree polynomial $f(x)$ in place of $\text{Id}(x)$. Under the Riemann hypothesis, we show that the error term, on average in a weak sense, over polynomials of arbitrary degree, is of the expected order $O_\varepsilon(N^{\frac{1}{4}+\varepsilon})$.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .